Trajectory of moving objects(II)

The trajectory of projectile depends on the initial velocity. Taking the two-dimension case as an example, we will demonstrate how to calculate the range and find the angle corresponding to max range.

(1)  Trajectory of projectile with/without friction

Given the inital angle, we can obtain the velocity along x and y axis at t=0. For the projectile, the trajectory will be not meaningful when y<0 since it is on the ground. Thus, we use the "while -- end " loop. At the beginning, y(t=0) i.e. y(1)=0. y(i)+eps>0 is true and it will start the iteration. Along x axis, the velocity remains the same while it is a motion with same acceleration along y axis.

clear
v=10;theta=pi/5;g=9.8;
vx(1)=v*cos(theta);vy(1)=v*sin(theta);
x(1)=0;y(1)=0;t(1)=0;dt=0.01;
i=1;
while y(i)+eps>0
  vx(i+1)=vx(i);
  vy(i+1)=vy(i)-g*dt;
  x(i+1)=x(i)+vx(i+1)*dt;
  y(i+1)=y(i)+vy(i+1)*dt;
  t(i+1)=t(i)+dt;
  i=i+1;
end

When the friction is considered, the forces along x and y axis can be obtained from the angle between vx and v, which should be updated at every iteration.

(2) Landing point

The landing point is the x_L value with y_L=0. However, in most calculations, we will find y(i)>0 and y(i+1)<0. Suppose the slope is the same when dt is small enough.

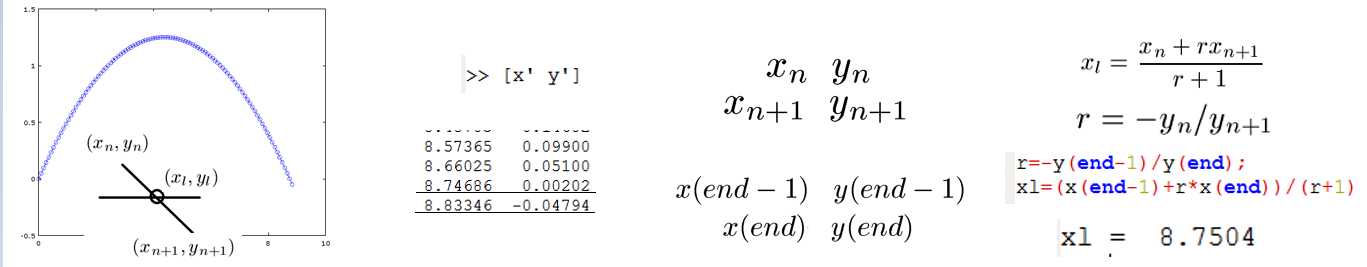
 Thus, we can obtain the range when the inital velocity is given.

(3) Angle of max range

In the following, we will write a function to find the angle which will make the range max.

function xL=motionfun(theta)
v=10;g=9.8;
vx(1)=v*cos(theta);vy(1)=v*sin(theta);
x(1)=0;y(1)=0;t(1)=0;dt=0.01;
i=1;
while y(i)+eps>0
  vx(i+1)=vx(i);
  vy(i+1)=vy(i)-g*dt;
  x(i+1)=x(i)+vx(i+1)*dt;
  y(i+1)=y(i)+vy(i+1)*dt;
  t(i+1)=t(i)+dt;
  i=i+1;
end
r=-y(end-1)/y(end);
xL=(x(end-1)+r*x(end))/(r+1);

For the function in Octave, the file name should be the same with the function. As shown above, we can obtain various range as a function of the intial angle theta. Then, we can find the angle corresponding to max range.

clear
theta=linspace(0,pi/2,11);
for i=1:length(theta)
  y(i)=motionfun(theta(i));
endfor
plot(theta,y,‘o-‘)

Trajectory of moving objects(II)

原文：https://www.cnblogs.com/xbyang99/p/11741804.html