贝叶斯公式由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展,用来描述两个条件概率之间的关系,比如 P(A|B) 和 P(B|A)。按照乘法法则,可以立刻导出:P(A∩B) = P(A)*P(B|A)=P(B)*P(A|B)。如上公式也可变形为:P(A|B)=P(B|A)*P(A)/P(B)。由于其有着坚实的数学基础,贝叶斯分类算法的误判率是很低的。贝叶斯方法的特点是结合先验概率和后验概率,即避免了只使用先验概率的主观偏见,也避免了单独使用样本信息的过拟合现象。贝叶斯分类算法在数据集较大的情况下表现出较高的准确率,同时算法本身也比较简单。

贝叶斯(Thomas Bayes,1702—1761),英国牧师、业余数学家。生活在18世纪的贝叶斯生前是位受人尊敬的英格兰长老会牧师。为了证明上帝的存在,他发明了概率统计学原理,遗憾的是,他的这一美好愿望至死也未能实现。贝叶斯在数学方面主要研究概率论。他首先将归纳推理法用于概率论基础理论,并创立了贝叶斯统计理论,对于统计决策函数、统计推断、统计的估算等做出了贡献。1763年发表了这方面的论著,对于现代概率论和数理统计都有很重要的作用。1758年发表了另一著作《机会的学说概论》。贝叶斯所采用的许多术语都被沿用至今。贝叶斯思想和方法对概率统计的发展产生了深远的影响。今天,贝叶斯思想和方法在许多领域都获得了广泛的应用。从二十世纪20~30年代开始,概率统计学出现了“频率学派”和“贝叶斯学派”的争论,至今,两派的恩恩怨怨仍在继续。
朴素贝叶斯分类是基于贝叶斯概率的思想,假设属性之间相互独立,求得各特征的概率,最后取较大的一个作为预测结果。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。简而言之,朴素贝叶斯是较为简单的一种分类器。
属性独立性:事件B的发生不对事件A的发生造成影响,这样的两个事件叫做相互独立事件。然而其属性独立性假设在现实世界中大多不能成立,例如: “spring”的后面更有可能跟着“MVC”。
A和B中至少有一件事情发生:A∪B; A与B同时发生:A∩B(或AB);如果P(AB) =P(A)P(B),称A,B 相互独立。即:从数学上说,若N (N≥2) 个事件相互独立,则必须满足这样的条件:其中任意k (N ≥ k ≥2)个事件同时发生的概率等于该k个事件单独发生时的概率的乘积。
例:假设事件相互独立,P(spring) = 0.2,P(MVC) = 0.8, 则 P(spring MVC) = 0.2 * 0.8=0.16
逻辑回归通过拟合曲线(或者学习超平面)实现分类,决策树通过寻找最佳划分特征进而学习样本路径实现分类,支持向量机通过寻找分类超平面进而最大化类别间隔实现分类。相比之下,朴素贝叶斯另辟蹊径,通过考虑特征概率来预测分类。
举个例子:现在有100个人,鱼龙混杂,好人和坏人的个数都差不多。现在要利用他们来训练一个“坏蛋识别器”。这时应该怎么办呢?我们不管他们之前干过什么事,只单看他们的长相。也就是说,我们在区别好人坏人时,只考虑他们的样貌特征。比如说“笑”这个特征,它可以是“甜美的笑”、“随和的笑”、“憨厚的笑”、“没心没肺的笑”、“微笑”等等,这些更可能是“好人的笑”;也可以是“阴险的笑”、“不怀好意的笑”、“色眯眯的笑”、“冷笑”、“皮笑肉不笑”等等,这些更可能是“坏人的笑”。单单就“笑”这个特征来说,一个好人发出“好人的笑”的概率更大,频率更高;而坏人则是发出“坏人的笑”的概率更大,频率更高。当然,好人也有发出坏笑的时候,坏人也有发出好人的笑的时候,这些就都是噪声了。
除了笑之外,这里可以用的特征还有纹身,性别等。朴素贝叶斯把类似“笑”这样的特征概率化,构成一个“人的样貌向量”以及对应的“好人/坏人标签”,训练出一个标准的“好人模型”和“坏人模型”,这些模型都是各个样貌特征概率构成的。这样,当一个品行未知的人来了以后,我们可以迅速获取他(她)的样貌特征向量,分别输入“好人模型”和“坏人模型”,输出两个概率值。如果“坏人模型”输出的概率值大一些,那这个人很有可能就是个坏人了。
决策树又是怎么做的呢?决策树可能先看性别,因为它发现给定的带标签人群里面坏人中男性更多,这个特征眼下最能区分坏人和好人,然后按性别先把一拨人分成两拨;接着看“笑”这个特征,因为它是接下来最有区分度的特征,根据不同的“笑”再把两拨人分成四拨;接下来看纹身......最后发现好人要么在学堂读书,要么在田里种地,要么在山上砍柴。而坏人呢,要么在大街上溜达,要么在地下买卖白粉,要么在海里当海盗。这些有次序的特征就像路上的一个个垫脚石(树的节点)一样,构成通往不同地方的路径(树的枝丫),这些不同路径的目的地(叶子)就是一个类别容器,包含了一类人。一个品行未知的人来了,按照其样貌特征顺序及其对应的特征值,不断走啊走,最后走到了学堂或农田,那就是好人;走到了地下或大海,那就是坏人。可以看出来,两种分类模型的原理是很不相同的。
【例】给定如下数据:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
帅 |
好 |
穷 |
上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
富 |
不上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
富 |
上进 |
嫁 |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
现在我们的问题是,假设有一对男女朋友,男生向女生求婚,此男生的四个特点分别是不帅,性格不好,穷,不上进,请你来判断一下该女生是嫁还是不嫁?
这是一个经典的分类问题,转换为数学问题就是比较p(嫁|(不帅、性格不好、穷、不上进))和p(不嫁|(不帅、性格不好、穷、不上进))的概率,就能给出嫁或者不嫁的答案!
这里我们运用到朴素贝叶斯公式:
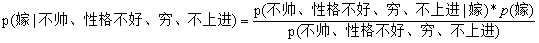
我们需要求p(嫁|(不帅、性格不好、穷、不上进)),这是我们现在不知道的,但是通过朴素贝叶斯公式可以转化为三个较为简单的量:
p(不帅、性格不好、穷、不上进|嫁)、p(不帅、性格不好、穷、不上进)、p(嫁)。
p(不帅、性格不好、穷、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(穷|嫁)*p(不上进|嫁),那么我们就要从给定的数据中分别统计出右边这几个概率,就可以求出左边的概率!
我们将上面的公式整理一下,得到:
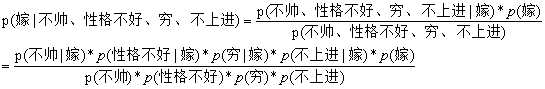
接下来我们一个一个地进行统计计算。
p(嫁)=?
首先我们整理的训练数据中,嫁的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
好 |
穷 |
上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
富 |
不上进 |
嫁 |
|
不帅 |
好 |
中 |
上进 |
嫁 |
|
帅 |
好 |
中 |
上进 |
嫁 |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
则 p(嫁) = 6/12(总样本数) = 1/2
接下来求p(不帅|嫁)=?
嫁的情况下不帅的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
不帅 |
好 |
中 |
上进 |
嫁 |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
则p(不帅|嫁) = 3/6 = 1/2
再求p(性格不好|嫁)= ?
嫁的情况下性格不好的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
则p(性格不好|嫁)= 1/6
求p(穷|嫁) = ?
嫁的情况下穷的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
好 |
穷 |
上进 |
嫁 |
则p(穷|嫁) = 1/6
再求p(不上进|嫁) = ?
嫁的情况下不上进的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
好 |
富 |
不上进 |
嫁 |
则p(不上进|嫁) = 1/6
下面开始求分母,p(不帅),p(性格不好),p(矮),p(不上进)
统计样本如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
帅 |
好 |
穷 |
上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
富 |
不上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
富 |
上进 |
嫁 |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
不帅统计如上标黄所示,占5个,那么p(不帅) = 5/12
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
帅 |
好 |
穷 |
上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
富 |
不上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
富 |
上进 |
嫁 |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
性格不好统计如上标黄所示,占4个,那么p(性格不好) = 4/12 = 1/3
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
帅 |
好 |
穷 |
上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
富 |
不上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
富 |
上进 |
嫁 |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
穷统计如上标黄所示,占7个,那么p(穷) = 7/12
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
帅 |
好 |
穷 |
上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
富 |
不上进 |
嫁 |
|
不帅 |
好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
富 |
上进 |
嫁 |
|
不帅 |
不好 |
富 |
上进 |
嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
不上进统计如上标黄所示,占5个,那么p(不上进) = 5/12
到这里,要求p(不帅、性格不好、穷、不上进|嫁),所需要的所有项全部求出来了,下面我们带入数据进去即可算出:
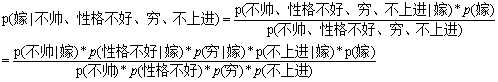
=(1/2*1/6*1/6*1/6*1/2)/(5/12*1/3*7/12*5/12)
下面我们根据同样的方法来求p(不嫁|不帅,性格不好,穷,不上进),完全一样的做法,为了加深理解,我们再来过一遍。首先公式如下:

下面我们也一个一个地来进行统计计算,这个公式里面,分母和上一个公式是一样的,所以我们不需要再算一次分母了,只需算分子部分。
p(不嫁)=?
首先我们整理的训练数据中,不嫁的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
则p(不嫁)= 6/12(总样本数) = 1/2
p(不帅|不嫁) = ?
不嫁的情况下不帅的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
则p(不帅|不嫁) = 2/6 = 1/3
p(性格不好|不嫁) = ?
不嫁的情况下性格不好的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
则p(性格不好|不嫁) = 3/6 = 1/2
p(穷|不嫁) = ?
不嫁的情况下穷的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
好 |
穷 |
上进 |
不嫁 |
|
帅 |
不好 |
穷 |
上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
则p(矮|不嫁) = 6/6 = 1
p(不上进|不嫁) = ?
不嫁的情况下不上进的样本数如下:
|
帅? |
性格? |
财富? |
上进? |
嫁不嫁? |
|
帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
不帅 |
不好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
|
帅 |
好 |
穷 |
不上进 |
不嫁 |
则p(不上进|不嫁) = 4/6 = 2/3
那么根据公式:

=(1/3*1/2*1*2/3*1/2)/(5/12*1/3*7/12*5/12)
很显然(1/3*1/2*1*2/3*1/2) > (1/2*1/6*1/6*1/6*1/2)
于是有p(不嫁|不帅、性格不好、穷、不上进) > p(嫁|不帅、性格不好、穷、不上进)
所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁!
原文:https://www.cnblogs.com/zhahuhu/p/11745628.html