(注:本篇博文是对《统计学习方法》中决策树一章的归纳总结,下列的一些文字和图例均引自此书~)
决策树(decision tree)属于分类/回归方法。其具有可读性、可解释性、分类速度快等优点。决策树学习包含3个步骤:特征选择、决策树生成、决策树修剪(剪枝)。
假设训练集为
$$D=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\},$$
其中$x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T$为输入实例(特征向量),$n$为特征个数,$y_i \in \{1,2,\cdots,K\}$为类标记,$i=1,2,\cdots, N$为样本容量。根据训练集构建一个决策树模型,使得能够对于输入$x_i$,给出预测的分类$y_i$。
决策树学习通常是一个递归选择最优特征,并根据该特征对训练数据机型分割,使得对各个之数据集有一个最好的分类的过程。其算法可以描述为如下过程:
经过上述过程之后,所有训练数据都被分到叶结点上,即都有了明确的分类,这就生成了一颗决策树。注意到,对于训练集能够进行正确分类的决策树可能有多个,也可能没有,我们需要的只是一个与训练集矛盾较小的决策树,同时具有很好的泛化能力(不仅仅对训练集有好的拟合,对测试集也应该有很好的预测)。从所有可能的决策树中选取最优决策树是NP完全问题,因此在实际中的决策树学习算法通常采用启发式方法,近似求解这一最优化问题,这样子得到的决策树是次最优的。
首先需要注意到,如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。可以通过信息增益或信息增益比来作为特征选择的准则。在介绍特征选择算法之前,需要先明确熵、条件熵、信息增益以及信息增益比几个概念。
定义(熵):在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量。设$X$是一个取有限个值得离散随机变量,其概率分布为
$$P(X=x_i)=p_i,\ i=1,2,\cdots,n$$
则随机变量$X$的熵定义为
$$H(X)=-\sum_{i=1}^{n}p_i\ log\ p_i,$$
注意到,熵只依赖于$X$的分布,而与$X$的取值无关,所以也可将$X$的熵记作$H(p)$,即
$$H(p)=-\sum_{i=1}^{n}p_i\ log\ p_i,$$
熵越大,随机变量的不确定性就越大。
(注:当熵的概率由数据估计(特别是极大似然估计)得到时,称为经验熵(empirical entropy))
举例,当$X$只取两个值时(取0和1),则$X$的概率分布为
$$P(X=1)=p,\ P(X=0)=1-p,\ 0\leq p\leq 1$$
熵为
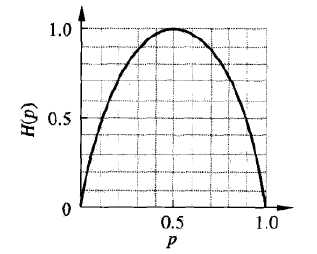
$$H(p)=-p\ log_2\ p-(1-p)\ log_2\ (1-p)$$
此时$H(p)$随$p$变化曲线如下图所示。可以看到,当$p=0$或$p=1$时,$H(p)=0$,随机变量完全没有不确定性;当$p=0.5$时,$H(p)=1$,此处熵最大,随机变量不确定最大。
定义(条件熵):假设有随机变量$(X,Y)$,其联合分布为
$$P(X=x_i,Y=y_i)=p_{ij},\ i=1,2,\cdots,n;\ j=1,2,\cdots,m$$
条件熵$H(Y|X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性。随机变量$X$给定的条件下随机变量$Y$的条件熵(conditional entropy)$H(Y|X)$,定义为$X$给定条件下$Y$的条件概率分布的熵对$X$的数学期望
$$H(Y|X)=\sum_{i=1}^nP(X=x_i)H(Y|X=x_i),\ i=1,2,\cdots,n$$
(注:当条件熵的概率由数据估计(特别是极大似然估计)得到时,称为条件经验熵(empirical conditional entropy))
信息增益(information gain)表示得知特征$X$的信息而使得类$Y$的信息的不确定性减少的程度。
定义(信息增益):特征$A$对训练数据集$D$的信息增益$g(D,A)$,定义为集合$D$的经验熵$H(D)$与特征$A$给定条件下$D$的经验条件熵$H(D|A)$之差,即
$$g(D,A)=H(D)-H(D|A)$$
信息增益值得大小取决于训练数据,没有绝对意义。比如在分类问题困难的是否,训练集本身的经验熵就很大,从而使得信息增益值也偏大。反之,信息增益值会偏小。可以使用信息增益比(information gain ratio)来进行校正。
定义(信息增益比):特征$A$对训练数据集$D$的信息增益比$g_R(D,A)$,定义为其信息增益$g(D,A)$与训练数据$D$的经验熵$H(D)$之比,即
$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$
决策树学习过程中需要利用信息增益(或信息增益比)选择特征。
比如,给定训练数据集$D$和特征$A$,经验熵$H(D)$表示对数据集$D$进行分类的不确定性,而经验条件熵$H(D|A)$表示在特征$A$给定的条件下对数据集$D$进行分类的不确定性。那么他们之间的差(信息增益)或者进一步的校正(信息增益比),就是表示由于特征$A$而使得对数据集$D$的分类的不确定性减少的程度。
因此,特征选择的原则是,选择信息增益(信息增益比)更大的特征,这样子的特征具有更强的分类能力。
ID3算法采用信息增益作为特征选择的依据。
输入:数据集$D$,特征集$A$,阈值$\varepsilon$。
输出:决策树$T$。
其算法过程可描述如下:
C4.5算法只是修改了ID3的特征选择方式,改成采用信息增益比选择特征,其余过程均一样。
输入:数据集$D$,特征集$A$,阈值$\varepsilon$。
输出:决策树$T$。
其算法过程可描述如下:
采用决策树生成算法生成的决策树可能存在分类过细,过拟合训练数据的问题,为了提高泛化能力,可以对于构建出的过于复杂的决策树进行简化(即剪枝),来得到低复杂度的决策树。
决策树剪枝通过极小化决策树整体的损失函数来实现。其中损失函数定义为
$$C_{\alpha}(T)=\sum_{t=1}^{\left |T\right|}N_tH_t(T)+\alpha\left| T\right |$$
其中$\left| T \right |$表示树$T$的叶结点个数,$t$是树$T$的叶结点,该叶结点有$N_t$个样本,$H_t(T)$为叶结点$t$上的经验熵,$\alpha\geq 0$是一个权衡决策树在训练集上精度以及自身复杂的的参数。
对于第$t$个叶结点,其中$k$类的样本点有$N_{tk}$个,$k=1,2,\cdots,K$,则该叶结点的经验熵可以描述为
$$H_t(T)=-\sum_k\frac{N_{tk}}{N_t}log\frac{N_{tk}}{N_t}$$
则损失函数可以写成如下形式
$$C_{\alpha}(T)=\sum_{t=1}^{\left |T\right|}N_tH_t(T)+\alpha\left| T\right |=\sum_{t=1}^{\left |T\right|}N_t\left (-\sum_{k=1}^K\frac{N_{tk}}{N_t}log\frac{N_{tk}}{N_t} \right )+\alpha\left| T\right |=-\sum_{t=1}^{\left | T\right |}\sum_{k=1}^{K}N_{tk}log\frac{N_{tk}}{N_t}+\alpha\left| T\right |=C(T)+\alpha\left| T\right |,$$
其中,$C(T)$表示该决策树对于训练数据的预测误差,$\left | T\right |$表示模型的复杂度。因此,当选取较大的$\alpha$时,可以促使选择较简单的模型(树);当选取较小的$\alpha$时,可以促使选择较复杂的模型(树)。
输入:决策树生成算法生成的决策树$T$,参数$\alpha$
输出:剪枝之后的子树$T_{\alpha}$
原文:https://www.cnblogs.com/CZiFan/p/11747613.html