leetcode的题目
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
这是一个动态规划的题目
wiki上的递推公式如下
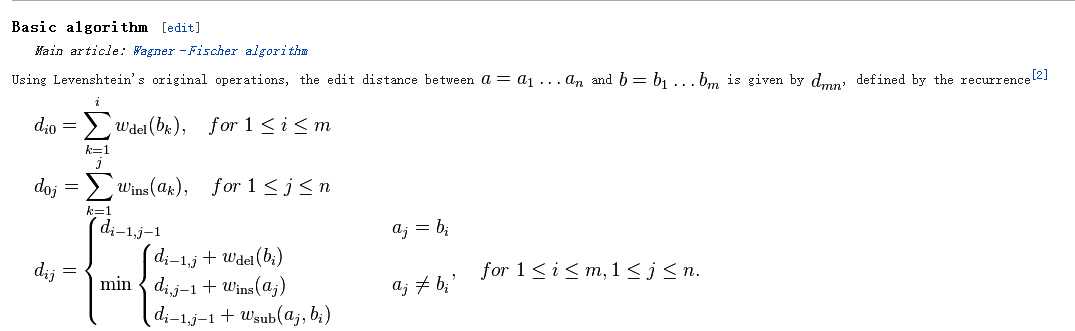
代码如下
1 int minDistance(string word1, string word2) { 2 int **dp = new int*[word1.length() + 1]; 3 for(int i = 0; i < word1.length() + 1; i ++) 4 dp[i] = new int[word2.length() + 1]; 5 6 for(int i = 0; i < word1.length() + 1; i ++) 7 dp[i][0] = i; 8 for(int i = 0; i < word2.length() + 1; i ++) 9 dp[0][i] = i; 10 11 for(int i = 1; i < word1.length() + 1; i ++) 12 for(int j = 1; j < word2.length() + 1; j ++) 13 { 14 dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1;//insert or delete 15 16 if(word1[i - 1] != word2[j - 1])//modify 17 { 18 dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + 1); 19 } 20 else 21 { 22 dp[i][j] = min(dp[i][j], dp[i - 1][j - 1]); 23 } 24 } 25 26 return dp[word1.length()][word2.length()]; 27 }
时间复杂度和空间复杂度都是O(M*N)
如果不要求计算修改过程, 那么空间复杂度可以优化到线性
感觉自己对动态规划还是很不敏感
查阅相关资料后发现, 这个题目属于文本比较算法, 还有很多相关的内容, 比如说LCS和一些其他更加高级的算法, 以后有空再研究一下
原文:http://www.cnblogs.com/stevenczp/p/3928087.html