题意:
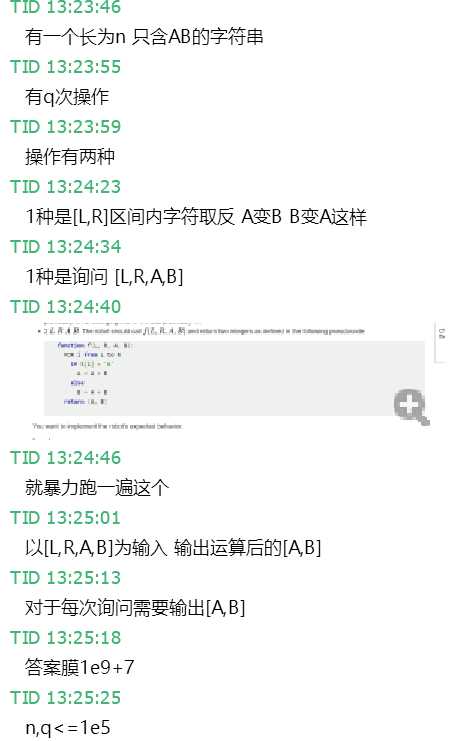
思路:因为线段树上每一段的矩阵之积只有两种,预处理一下,翻转的时候下传tag然后把另一种可能性换上来就好
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 typedef unsigned int uint; 5 typedef unsigned long long ull; 6 typedef long double ld; 7 typedef pair<int,int> PII; 8 typedef pair<ll,ll> Pll; 9 typedef vector<int> VI; 10 typedef vector<PII> VII; 11 //typedef pair<ll,ll>P; 12 #define N 200010 13 //#define M 200010 14 #define INF 1e9 15 #define fi first 16 #define se second 17 #define MP make_pair 18 #define pb push_back 19 #define pi acos(-1) 20 #define mem(a,b) memset(a,b,sizeof(a)) 21 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++) 22 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--) 23 #define lowbit(x) x&(-x) 24 #define Rand (rand()*(1<<16)+rand()) 25 #define id(x) ((x)<=B?(x):m-n/(x)+1) 26 #define ls p<<1 27 #define rs p<<1|1 28 29 const ll MOD=1e9+7,inv2=(MOD+1)/2; 30 double eps=1e-6; 31 int dx[4]={-1,1,0,0}; 32 int dy[4]={0,0,-1,1}; 33 34 struct Ma 35 { 36 int n=2,m=2; 37 ll a[2][2]; 38 void init() 39 { 40 n=m=0; 41 mem(a,0); 42 } 43 Ma operator +(Ma b) const 44 { 45 Ma c; 46 c.n=n; c.m=m; 47 rep(i,0,n-1) 48 rep(j,0,m-1) c.a[i][j]=a[i][j]+b.a[i][j]; 49 return c; 50 } 51 Ma operator *(Ma b) const 52 { 53 Ma c; 54 c.init(); 55 c.n=n; c.m=b.m; 56 rep(i,0,n-1) 57 rep(j,0,b.m-1) 58 rep(k,0,m-1) c.a[i][j]=(c.a[i][j]+a[i][k]*b.a[k][j]%MOD)%MOD; 59 return c; 60 } 61 }; 62 63 Ma t[N<<2][2],M[2],one,ans; 64 int b[N],tag[N]; 65 char s[N]; 66 67 int read() 68 { 69 int v=0,f=1; 70 char c=getchar(); 71 while(c<48||57<c) {if(c==‘-‘) f=-1; c=getchar();} 72 while(48<=c&&c<=57) v=(v<<3)+v+v+c-48, c=getchar(); 73 return v*f; 74 } 75 76 void pushdown(int p) 77 { 78 if(tag[p]) 79 { 80 swap(t[ls][0],t[ls][1]); 81 swap(t[rs][0],t[rs][1]); 82 tag[ls]^=1; 83 tag[rs]^=1; 84 tag[p]=0; 85 } 86 } 87 88 void pushup(int p) 89 { 90 t[p][0]=t[ls][0]*t[rs][0]; 91 t[p][1]=t[ls][1]*t[rs][1]; 92 } 93 94 void build(int l,int r,int p) 95 { 96 if(l==r) 97 { 98 t[p][0]=M[b[l]]; 99 t[p][1]=M[b[l]^1]; 100 tag[p]=0; 101 return; 102 } 103 int mid=(l+r)>>1; 104 build(l,mid,ls); 105 build(mid+1,r,rs); 106 pushup(p); 107 108 } 109 110 void update(int l,int r,int x,int y,int p) 111 { 112 if(x<=l&&r<=y) 113 { 114 tag[p]^=1; 115 swap(t[p][0],t[p][1]); 116 return; 117 } 118 pushdown(p); 119 int mid=(l+r)>>1; 120 if(x<=mid) update(l,mid,x,y,ls); 121 if(y>mid) update(mid+1,r,x,y,rs); 122 pushup(p); 123 } 124 125 Ma query(int l,int r,int x,int y,int p) 126 { 127 if(x<=l&&r<=y) return t[p][0]; 128 pushdown(p); 129 int mid=(l+r)>>1; 130 Ma res=one; 131 if(x<=mid) res=res*query(l,mid,x,y,ls); 132 if(y>mid) res=res*query(mid+1,r,x,y,rs); 133 return res; 134 } 135 136 int main() 137 { 138 //freopen("1.in","r",stdin); 139 int n=read(),q=read(); 140 scanf("%s",s+1); 141 rep(i,1,n) b[i]=s[i]-‘A‘; 142 M[0].n=M[0].m=M[1].n=M[1].m=one.n=one.m=ans.n=ans.m=2; 143 M[0].a[0][0]=M[0].a[1][0]=M[0].a[1][1]=1; 144 M[1].a[0][0]=M[1].a[0][1]=M[1].a[1][1]=1; 145 one.a[0][0]=one.a[1][1]=1; 146 build(1,n,1); 147 148 while(q--) 149 { 150 int op=read(); 151 if(op==1) 152 { 153 int x=read(),y=read(); 154 update(1,n,x,y,1); 155 } 156 else 157 { 158 int x=read(),y=read(),A=read(),B=read(); 159 Ma t=query(1,n,x,y,1); 160 // printf("t=\n"); 161 //rep(i,0,1) 162 //{ 163 // rep(j,0,1) printf("%I64d ",t.a[i][j]); 164 // printf("\n"); 165 //} 166 ans.a[0][0]=A; 167 ans.a[0][1]=B; 168 ans.a[1][0]=ans.a[1][1]=0; 169 ans=ans*t; 170 printf("%I64d %I64d\n",ans.a[0][0],ans.a[0][1]); 171 } 172 } 173 return 0; 174 }
【CF1252K】Addition Robot(线段树,矩阵乘法)
原文:https://www.cnblogs.com/myx12345/p/11749196.html