Sza-Template「POI 2005」

【题目描述】
Byteasar 想在墙上涂一段很长的字符,他为了做这件事从字符的前面一段中截取了一段作为模版. 然后将模版重复喷涂到相应的位置后就得到了他想要的字符序列.一个字符可以被喷涂很多次,但是一个位置不能喷涂不同的字符.做一个模版很费工夫,所以他想要模版的长度尽量小,求最小长度是多少.拿样例来说 ababbababbabababbabababbababbaba , 模版为前8个字符ababbaba，是最小的模板长度。

【输入格式】
输入一行最多不超过\(500000\)个，最少\(1\)个小写字符。

【输出格式】
一个数表示最小的模板长度。

有一说一 这题我又不会做

我是听了题解之后还挣扎了半天才理解的

前置知识：KMP
首先 把这个串的\(nxt\)数组(就是KMP里那个)求出来 然后建出这个串的\(fail\)树
在这里 我举一个例子来帮助理解这题
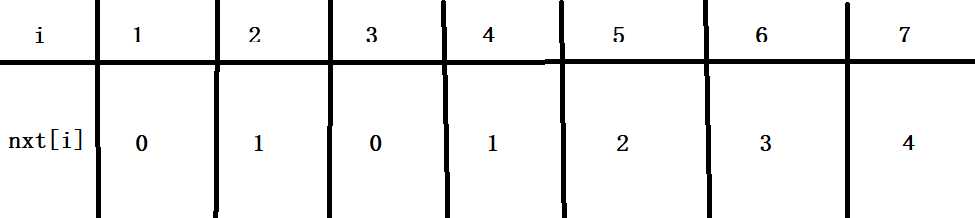
设给的串是 aabaaba 显然答案是4 即最小模板为 aaba

\(nxt\)数组

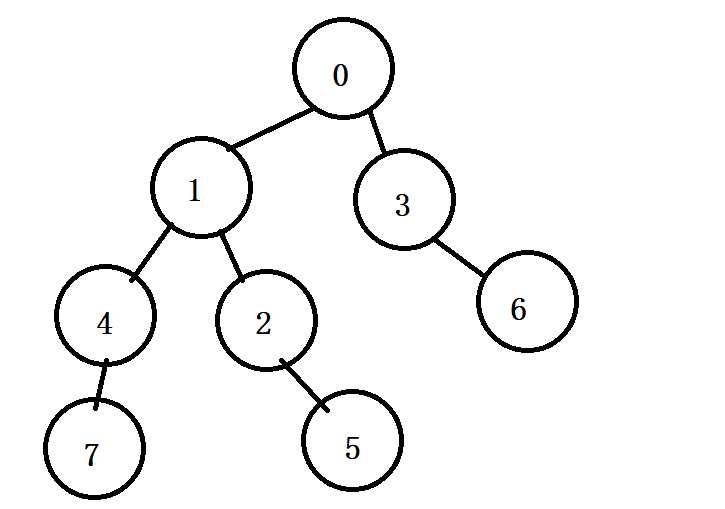
\(fail\)树(让每个\(i\)连向\(nxt[i]\))

我根本就不会画图

因为模板串必然是主串的一个前缀 也必然是主串的一个后缀 所以可能的答案只会在\(0\sim n\)的这条链上(不包括0)
再考虑一个问题 设主串为\(s\) \(fail\)树上的一个点\(i\) 对于它子树里的所有点\(j\) 一定满足\(s[1\sim i]\)是\(s[1\sim j]\)的一个后缀(有点绕) 为什么？不知道就再回去看看\(nxt\)数组的定义
所以我们可以等价理解为 当且仅当\(j\)是\(i\)子树中的一个节点时，我们可以把\(s[1\sim i]\) 喷涂在 \(j-i+1 \sim j\) 的位置上 即喷涂到一段以\(j\)结尾 长为\(i\)的区间上

-----分割线 理解之后继续看下面的--------

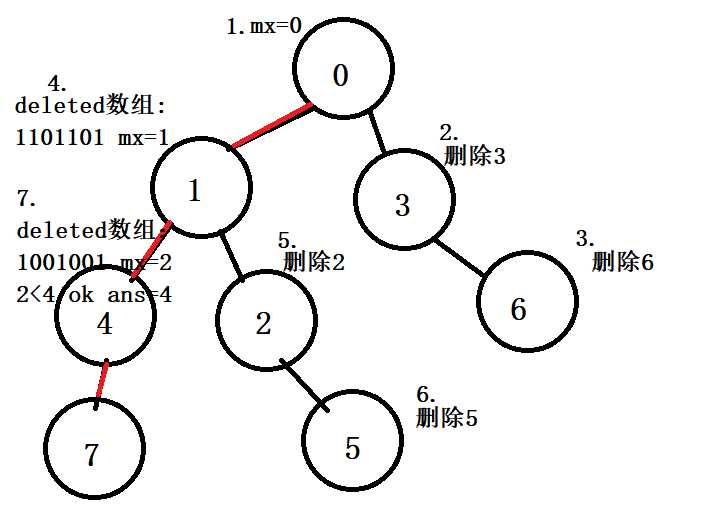
理解了这个之后 剩下的操作就比较简单了 把\(0 \sim n\) 链上的点全部打上标记 从\(0\)开始dfs，每次到一个点，遍历它所有的儿子节点 若一个儿子节点被标记了 就表示这是链上的下一个点 把它设为\(y\) 若一个儿子节点没有被标记 那就把它子树中(包括自己)所有的点\(j\)的\(deleted[j]\)设为1 \(deleted[j]=1\)表示\(s[1\sim y]\)这个串不能被喷涂在以\(j\)结尾的位置上
然后删除的时候顺便维护一下 当前最长的一段连续的\(deleted[j]\)都为1的有多长 记为\(mx\) 处理完所有子节点后向那个打了标记的子节点继续深搜 每到达一个打了标记的点\(x\)之后立即判断 若\(mx < x\) 即长为\(x\)的模板已经足够覆盖所有空缺处 \(x\)就是一个符合题意的答案 由于\(fail\)树的父节点一定比子节点编号小 所以链上第一个\(x\)就是最小答案

附：样例 程序实现过程

【代码】

#include <iostream>
#include <cstdio>
#include <cstring>
#define ri register int
using namespace std;

char ch[500005];
int n, the_nxt[500005];
int head[500005], pre[1000005], to[1000005], sz;
int pr[500005], nxt[500005];
bool mark[500005];
int mx, ans;

void insert(int u, int v) {
    pre[++sz] = head[u]; to[sz] = v; head[u] = sz;
}

void del(int x, int fa) {
    pr[nxt[x]] = pr[x]; nxt[pr[x]] = nxt[x];
    mx = max(mx, nxt[x] - pr[x] - 1);
    for (int i = head[x]; i; i = pre[i]) {
        int y = to[i];
        if (y == fa) continue;
        del(y, x);
    }
}

void dfs(int x, int fa) {
    if (x > mx) return ans = x, void();
    int nnxt;
    for (int i = head[x]; i; i = pre[i]) {
        int y = to[i];
        if (y == fa) continue;
        if (!mark[y]) del(y, x);
        else nnxt = y;
    }
    dfs(nnxt, x);
}

int main() {
    scanf("%s", ch + 1);
    n = strlen(ch + 1);
    for (ri i = 2, j = 0; i <= n; i++) {
        while (j && ch[j+1] != ch[i]) j = the_nxt[j];
        if (ch[j+1] == ch[i]) j++;
        the_nxt[i] = j;
    }
    for (ri i = 1; i <= n; i++) {
        insert(i, the_nxt[i]); insert(the_nxt[i], i);
    }
    for (ri i = n; i > 0; i = the_nxt[i]) mark[i] = 1;
    mark[0] = 1;
    for (ri i = 1; i <= n; i++) {
        pr[i] = i-1; nxt[i] = i+1;
    }
    dfs(0, 0);
    cout << ans << endl;
    return 0;
}

Sza-Template「POI 2005」

原文：https://www.cnblogs.com/ak-dream/p/AK_DREAM20.html