决策树 python代码实现 ID3,C4.5,CART方法

本代码来源自：https://github.com/Erikfather/Decision_tree-python 

1.数据集描述

共分为四个属性特征：年龄段，有工作，有自己的房子，信贷情况;  现根据这四种属性特征来决定是否给予贷款    

为了方便，我对数据集进行如下处理：

在编写代码之前，我们先对数据集进行属性标注。

（0）年龄：0代表青年，1代表中年，2代表老年；

（1）有工作：0代表否，1代表是；

（2）有自己的房子：0代表否，1代表是；

（3）信贷情况：0代表一般，1代表好，2代表非常好；

（4）类别(是否给贷款)：no代表否，yes代表是。

 存入txt文件中:

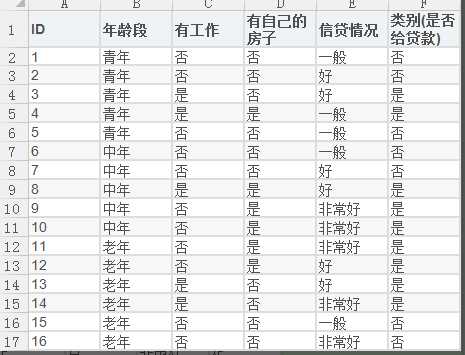
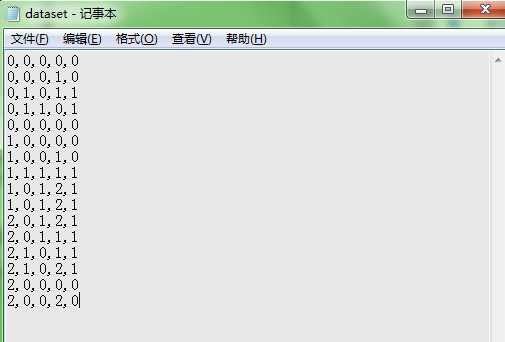
然后分别利用ID3，C4.5，CART三种算法对数据集进行决策树分类； 

数据集的读取：

def read_dataset(filename):
    """
    年龄段：0代表青年，1代表中年，2代表老年；
    有工作：0代表否，1代表是；
    有自己的房子：0代表否，1代表是；
    信贷情况：0代表一般，1代表好，2代表非常好；
    类别(是否给贷款)：0代表否，1代表是
    """
    fr = open(filename,‘r‘)
    all_lines = fr.readlines()  ## list形式,每行为1个str
    #print(all_lines)
    labels = [‘年龄段‘,‘有工作‘,‘有自己的房子‘,‘信贷情况‘]
    dataset = []
    for line in all_lines[0:]:
        line = line.strip().split(‘,‘)  #以逗号为分割符拆分列表
        dataset.append(line)
    return dataset,labels　　

运行一下，看看有什么效果：

dataset,labels = read_dataset(‘./data/dataset.txt‘)
print(dataset,labels)

[[‘0‘, ‘0‘, ‘0‘, ‘0‘, ‘0‘], [‘0‘, ‘0‘, ‘0‘, ‘1‘, ‘0‘], [‘0‘, ‘1‘, ‘0‘, ‘1‘, ‘1‘], [‘0‘, ‘1‘, ‘1‘, ‘0‘, ‘1‘], [‘0‘, ‘0‘, ‘0‘, ‘0‘, ‘0‘],
 [‘1‘, ‘0‘, ‘0‘, ‘0‘, ‘0‘], [‘1‘, ‘0‘, ‘0‘, ‘1‘, ‘0‘], [‘1‘, ‘1‘, ‘1‘, ‘1‘, ‘1‘], [‘1‘, ‘0‘, ‘1‘, ‘2‘, ‘1‘], [‘1‘, ‘0‘, ‘1‘, ‘2‘, ‘1‘], 
[‘2‘, ‘0‘, ‘1‘, ‘2‘, ‘1‘], [‘2‘, ‘0‘, ‘1‘, ‘1‘, ‘1‘], [‘2‘, ‘1‘, ‘0‘, ‘1‘, ‘1‘], [‘2‘, ‘1‘, ‘0‘, ‘2‘, ‘1‘], [‘2‘, ‘0‘, ‘0‘, ‘0‘, ‘0‘], 
[‘2‘, ‘0‘, ‘0‘, ‘2‘, ‘0‘]] [‘年龄段‘, ‘有工作‘, ‘有自己的房子‘, ‘信贷情况‘]

2. 计算信息熵

$Ent(D_{k})= \sum_{k=1}^{\left | y \right |}P_{k}\times log_{2}P_{k}$
- 其中$\left | y \right |$为样本的种类个数
该公式如何理解呢？比如说我现在数据集中有17个样本，一共有两个类别$\left | y \right |=2$，其中正样本个数为8个，负样本个数为9个，则根节点的信息熵为：$Ent(D_{k})= -\sum_{k=1}^{\left | y \right |}P_{k}\times log_{2}P_{k}=-(\frac{8}{17}\times log_{2}{\frac{8}{17}} + \frac{9}{17}\times log_{2}{\frac{9}{17}})$

def inforEntropy(dataset):
    m = len(dataset)   #数据集的长度
    labelCounts = {}   #给所有可能分类创建字典
    
    for featvec in dataset:
        currentlabel = featvec[-1]  #获取当前样本的label
        if currentlabel not in labelCounts.keys():
            labelCounts[currentlabel] = 0     
        labelCounts[currentlabel] += 1 # 统计每类标签的样本个数
        
        Ent=0.0 
        for key in labelCounts:
            p = float(labelCounts[key]) / m 
            Ent = Ent - p*log(p,2)
            
    return Ent 

决策树 python代码实现 ID3,C4.5,CART方法

原文：https://www.cnblogs.com/carlber/p/11772103.html