边界函数

根据成长函数的定义，猜测

   ——>break point K restricts maximum possible m_h(N) a lot for N>k

bounding functionB(N, k): maximum possible m_H(N) when break point = k

下面是一个填写表的过程

(1)根据一些简单的推导，得到一个如下所示的表格：

当B(2,2)表示有2个点，这两个点不能被shatter，最多有一个点被shatter，故B(2,2)=3

当B(3,2)表示有3个点，其中任意两个点不能被shatter，因此可以是(o,o,o)(o,o,x)(o,x,o)(x,o,o),故B(3,2)=4

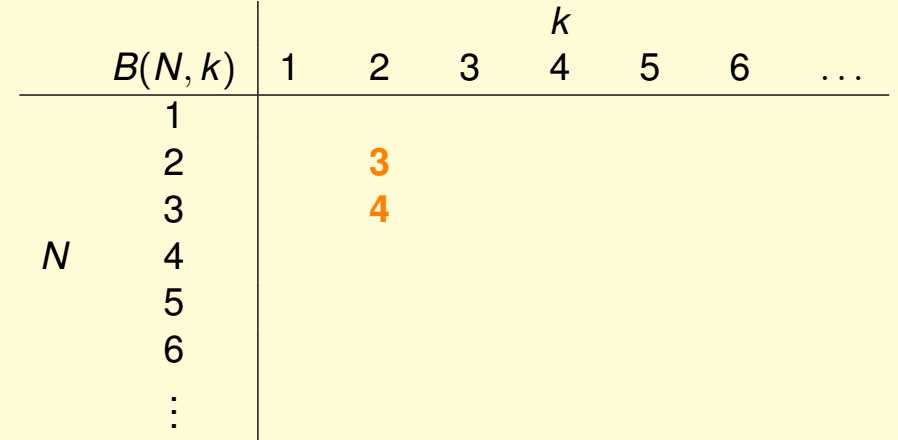
(2)对于break point=1的情况来说，无论有多少个点，有且仅有一条记录的样式，因为如果有不同的，则会产生大于一个数量的点背shatter

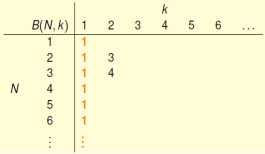
(3)对于任意的点来说，如果break point>n 则任意的点都不能内n个点都可以随便取，都不能被shatter掉，因此为B(N, k)=2ⁿ，

(4)对于对角线上的点，即有N个点任意的N-1个点都会被shatter掉，任意的N个点都不会被shatter掉，因此B(N, k)=2ⁿ-1

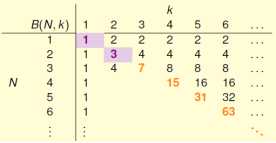
(5)对于剩余的点，其值的求解过程如示例一

(6)最后，根据示例一，可以得到如下结果

示例一：

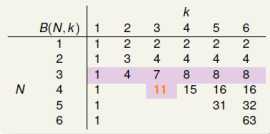
(1)以B(4,3)为例，4个输入中任意3个都不能被shatter，用一个简单的程序遍历所有2^16个划分组合得到B(4,3)=11。得到如下图所示：

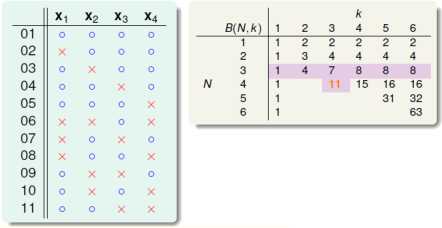
(2)将这11个划分分为2组啥，如下图所示

其中橙色的划分总能找到相似的伴侣，紫色的划分总是单身的，接着，如下图所示：

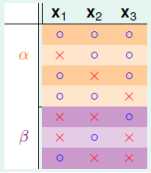
根据上图可知B(4,3)=11=2α+β,

由于k=3，所以（x1, x2, x3）不能被shatter：α+β≤B(3,3)

由于x4成对，且（x1, x2, x3, x4）不能shatter任意3个，所以（x1, x2, x3）不能shatter任意2个：α≤B(3,2)

所以：

               最终得到(6)中的结果。

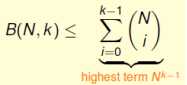   并且经过证明，坐式中的等号是恒成立的，证明过程省略。

把备选函数集H中备选函数的数量M用成长函数代替，正确的公式应该是：

这就是VC Bound： 

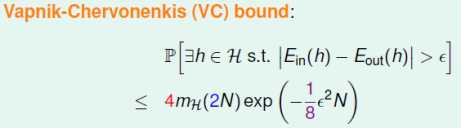
它提供了一个对机器学习结果可靠性的衡量，因为成长函数是N的多项式，所以BAD事件发生的概率随着N的增大而显著下降。

E_out≈E_in possible if m_H(N)breaks somewhere and N large enough.