描述性统计分析
定义
所谓描述性统计分析,就是对一组数据的各种特征进行分析,以便于描述测量样本的各种特征及其所代表的总体的特征。描述性统计分析的项目很多,常用的如平均数、标准差、中位数、频数分布、正态或偏态程度等等。这些分析是复杂统计分析的基础。
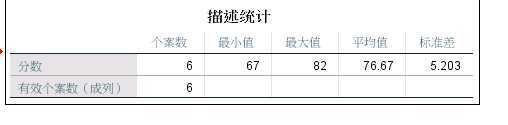
方差和标准差
标准差用来度量观测值偏离平均数的大小,相当于平均偏差,可以直接描述数据偏离均值的程度。
均值的标准误值
均值的标准误用来衡量不同样本的均值之间的差别。如果两个样本均值的差值与标准误的比值小于-2成大于2,则可以断定两个均值有显著的差别,进而断定这两个样本来自于两个不同的总体。
变异系数
概念:在比较两组数据离散程度大小时,如
果观测的测量尺度相差太大,成者是数据的量
纲不一样,这时直接比较二者的标准差并不合
迫,需要首先消除测量尺度和量纲的影响,变异
系数就可以剔除这些影响。
分位数
P%分位数是指使得至少有P%的数据小于成等于这个值,且使得至少有(100-P)%的数据大于或等于这个值/数据按照从小到大进行排序/最小的四分位数称为下四分位数,记为Q1,所有观测值中有1/4的观测值小于下四位数,3/4的观测值大于下四企数,中点住置的四分位数就是中位数.最大的四分位数称为上四分位数,记为Q3统计中常常把数据的最小值,下四分位数,中位数,上四分位数和最大值称为数据的总结五数。从这五个值可以大致看出数据分布的中心和离散程度。而箱图则是这五个数的图形表现.
分布的形状当Q>0时,分布为正偏和右偏,及分布图形在右边拖尾,分布图有很长的右尾尖锋偏左,a<0,分布为负片和左偏,及分布图形在左边拖尾,分布圈有很长的左尾,峰尖偏右,a=0,分布对称,不论正负哪种偏态,偏度的绝对值最大表示偏斜的程度越大,反之偏斜程度越小,分布形状越接近对称.
中新趋势的描述
装新趋势是指一组数据向某个中心值靠拢的倾向。在统计学中描述数据分布的中心位置的统计量称为位置统计量。对于连续变量(或称为尺度变量)和定序变量,描述数据中心趋势的指标,有均值、中位数、众数、5%截尾均值;对于定性数据(民意数据),描述数据中心趋势的指标只有众数
均值
均值一般是指数据的算术均值(算术平均数),是数据中心趋势的主要度量指标,也是实际问题中,使用最多的指标
数据的均值容易受极端值的影响
5%截尾均值
把观测值按照从小到大顺序排列,剔除掉排序后的数据,序列两端的部分数值后,计算得到的均值
中位数
将观测值按照从小到大的顺序排列,位于中间位置的数值称为中位数
众数
众数是观测值中出现次数最多的数值,即反映了这组观测值的集中趋势
极差
数据的观测值中的最大值与最小值之差反映了数据的波动情况
均值得标准误
如果两个样本均值的差值与标准误的比值,小于-2或大于2,则可以断定两个均值有显著的差别,进而断定这两个样本来,至于两个不同的总体
原文:https://www.cnblogs.com/liuchenrui1/p/11773875.html