二叉树:树的每个节点最多只能有两个子节点
上图的第一幅图B节点有DEF三个子节点,就不是二叉树,称为多路树;而第二幅图每个节点最多只有两个节点,是二叉树,并且二叉树的子节点称为“左子节点”和“右子节点”。上图的D,E分别是B的左子节点和右子节点。
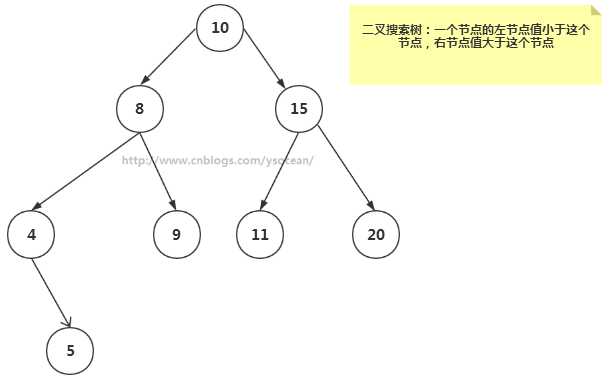
如果我们给二叉树加一个额外的条件,就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。
二叉搜索树要求:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
/**
* hash
* @param key
* @return
*/
private static <k> int getHashCode(k key){
int h;
//生成的hash值的随机性会增大
return (h = key.hashCode()) ^ (h >>> 16);
}
Node root;
class Node <k,v>{
private k key;
private v value;
private int hasKey; //节点数据
private Node leftChild; //左子节点的引用
private Node rightChild; //右子节点的引用
private int isDelete = 0; //是否删除
public Node(int hasKey,k key,v value){
this.hasKey = hasKey;
this.key = key;
this.value = value;
}
}
/**
* 查找节点
* @param key
* @return
*/
public Node find(Object key){
int hashKey = getHashCode(key);
if (root==null){
return root;
}
Node curr = root;
while (curr!=null){
if (curr.hasKey==hashKey){
return curr;
}else if (curr.hasKey>hashKey){
curr = curr.leftChild;
}else {
curr = curr.rightChild;
}
}
return null;
}
/**
* 插入新节点
* @param key
* @param value
* @return
*/
public Node insert(Object key,Object value){
int hashKey = getHashCode(key);
Node newNode = new Node(hashKey,key,value);
if (root==null){
root = newNode;
return newNode;
}
Node curr = root;
while (curr!=null){
Node parentNode = curr;
if (curr.hasKey>hashKey){
curr = curr.leftChild;
if (curr==null){
parentNode.leftChild = newNode;
}
}else {
curr = curr.rightChild;
if (curr==null){
parentNode.rightChild = newNode;
}
}
}
return newNode;
}
/**
* 删除节点
* @param key
* @return Node
*/
public Node delete(int key){
int hashKey = getHashCode(key);
Node curr = root;
while (curr!=null){
if (curr.hasKey==hashKey){
curr.isDelete=1;
return curr;
}else if (curr.hasKey>hashKey){
curr = curr.leftChild;
}else {
curr = curr.rightChild;
}
}
return null;
}
原文:https://www.cnblogs.com/wushenghfut/p/11776142.html