所谓高斯模糊,就是指一个图像与二维高斯分布的概率密度函数做卷积。它的效果如下:

是不是有点像变成了近视眼的感觉?没错,高斯模糊常常用来模拟人眼中的物体变远、变快的效果。在照片处理中,我们常常将背景施以高斯模糊,使得背景仿佛变远了,从而突出前景的人物或物体。一些所谓“先拍照,后对焦”的技术利用的也是高斯模糊这个效果。若想弄出视点飞快移动的效果,也可以对背景使用高斯模糊。在一些CG动画中,视点移动得越快,背景将被施以越重的高斯模糊,以模拟人的视觉特点。事实上,在早期对人眼的视觉特性研究中,就是使用高斯模糊为模型近似模拟人眼的特性。但是我们知道,人眼的原理十分复杂,并非一个函数就可以模拟得了的。实际上人眼的特性近似于一个带通滤波器,而非高斯模糊这样的低通滤波器。
说回高斯模糊。前面说了高斯模糊是指一个图像与二维高斯分布的概率密度函数做卷积。高斯分布即正态分布。由于图像是离散的,所以高斯分布的概率密度函数需要先做采样才能与图像进行卷积。
为简便起见,下面我们将“高斯分布的概率密度函数”简称为“高斯函数”,虽然它只是高斯函数的一个特例。真正的高斯函数为
若不特别强调,以下出现的“高斯函数”均指“高斯分布的概率密度函数”。
一维的高斯函数如下,其中μ为均值,σ为标准差。
在图像分析方面,通常只考虑μ为零的情况,即。
同样在μ为零的情况下,二维的高斯函数如下
注意到它可以看成是两个高斯函数的乘积
又注意到的存在,让我们直觉地感受到这个曲面有一个圆的结构存在。若令f(x,y)取一个常数值C,则上式可以画出一个圆。这意味着这个曲面的等高线是个圆。我们也可以把上式看成是以下高斯函数绕z轴旋转而成。
这说明了高斯函数的一个重要特性:圆周对称性(Circular symmetry),又叫做各向同性(Isotropy)
如前所述,为了能与离散的图像做卷积,我们必须对高斯函数进行采样。这个采样通常是限定在以x,y轴的原点为中心的一个正方形的区域内。采样的结果被称作“高斯核”(Gaussian kernel)。由于高斯模糊的普遍应用,如今计算一个高斯核已相当简单。不必说各种函数库,直接在网上找一个在线高斯核计算工具即可算出。但是若要深究其中的数学原理,却不是这么简单。下面将一步步说明高斯核究竟是怎么生成的。
一、采样方法
首先是如何采样。
采样的最简单的一个做法是直接取曲面上的值。例如,先把xy平面划分成许多1x1大小的方格子,直接取这些点上z值,便可完成采样。另一种采样方法是,令采样值z在1x1的格子上形成的立方柱的体积,等于该格子范围内的曲面下的体积。语言描述有些难懂,让我们来看一下一维的高斯函数,使用这两种采样方法的对比图。
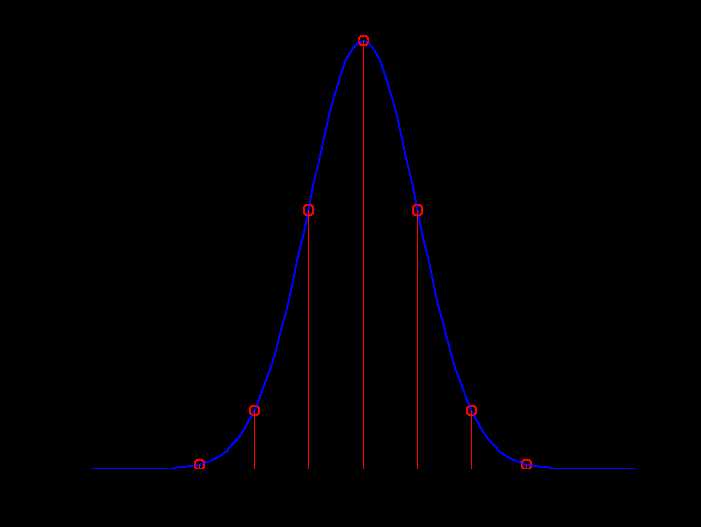
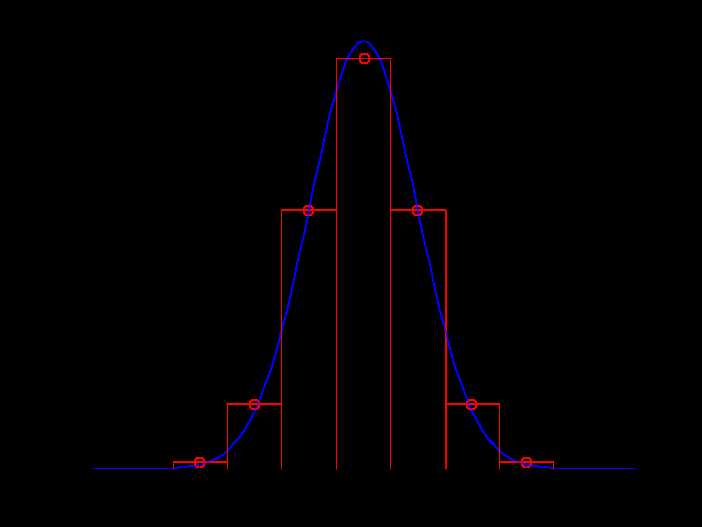
图(1) 直接取点采样 图(2) 积分式采样
图(1)是对一维的高斯函数直接取点采样。采样位置为x轴的整数点。图(2)的采样位置同样是x轴的整数点,但并不是直接取该点的函数值,而是令红色矩形的面积等于该范围内曲线下方的面积。这种采样方法的特点是更好地近似了曲线的积分特性。若采样后要对采样值进行某些加法(或者加权加法)运算,使用第2种采样法更合适。两种方法本无优劣之分,到底该使用哪种方法一切要看我们后面如何使用这些采样值。如前所述,我们求得高斯核之后最终是要与输入图像做卷积。卷积在连续域是一种积分形式,在离散域是一种加权求和,所以应使用第2种采样法比较合适。我们不难想象把一维高斯函数扩展到二维高斯函数的情景,其实也就是将红色矩形变成红色立方体,将曲线下的面积变为曲面下的体积而已。
二、高斯核的形状和大小
确定了采样方法后,还要确定高斯核的形状和大小。最常用的高斯核是n×n的正方形,根据应用的不同,也可以采用菱形或者近似圆形。这里就只介绍最常用的正方形高斯核。
正方形的边长n该如何确定呢?工程上常用的是取。3σ和6σ都是统计学上常用的大数指标。它的数学意义是:在
的范围内,正态分布曲线下的面积约等于整条曲线下面积的93.3%;在
的范围内,正态分布曲线下的面积约等于整条曲线下面积的99.99966%。在不同精度的应用场景下,3σ以外或者6σ以外的部分通常被认为是可以忽略的部分。由于高斯核是要与输入图像作卷积,其中间大周围小的特性,正是为了给予靠近核中心的像素更大的权重、给远离核中心的像素更小的权重。(为什么?因为若是采用同等权重,当一个离核中心很远的像素若刚好有很大的值,就会影响整个卷积结果,这不符合人的直观感受,因此越远的像素应该给卷积结果带来越少的影响。)当像素离核中心的距离超过3σ时,通常认为其对中心的影响已不大,可以忽略。
为了使高斯核有一个明确的“中心”,n通常取奇数。由于3σ不一定是整数,所以可以令n等于离3σ最近的奇数。当然也可以用向上圆整或者向下圆整,前者更注重精度,后者更注重减少计算量。你也可以无视什么3σ原理,自己取任意奇数,在数学上也没什么不可以的。
三、高斯核的计算
确定了采样方法、高斯核的形状和大小,总算可以计算高斯核了。例如,取σ=1.5,n=5,根据上面说的积分式采样方法,可以得到如下高斯核:

我们可以观察到其中的圆周对称性。虽然不怎么好看,但总算大功告成了吧?且慢!既然高斯核要与输入图像作卷积,那么还得考虑像素值的溢出问题。我们常用的像素是的8位色的像素(或子像素),其取值范围是0~255。输入图像与高斯核作卷积之后的像素值不能超过这个范围。怎么办呢?我们对高斯核的每个元素除以一个常数,这个常数等于高斯核中所有元素之和。

这样就相当于对输入图像的像素做了加权平均。根据加权平均的性质,一组数字进行加权平均的结果,不会大于该组数字中的最大数,也不会小于该组数字中的最小数。这样就保证了卷积结果不会溢出了。等等!那个“所有元素之和”的常数怎么那么接近1?这是当然的了,因为高斯函数在整个曲线下的面积等于1(在二维的情况下,整个曲面下的体积等于1),所以所有元素之和自然就接近1了。也就是说,高斯核无需除以常数也可以保证卷积结果不会溢出。这里之所以要拿出来强调,是因为并非所有核都有高斯核这样好的性质,处理溢出问题切不可忘。
也许是因为数字工程师厌恶小数,高斯核还有种常见的形式是将各个元素变成整数。具体做法是,将最小的四个角的元素设为1,其他元素按比例放大并圆整,最后在高斯核前除以所有元素之和,结果如下:

这个核看起来“整洁”多了。它跟上面的核只有一些精度上的差别,没有本质上的差别。
四、高斯核以及高斯模糊的快速计算
以上的计算均是按照定义进行的计算,由于高斯模糊的广泛应用,我们需要更快更省资源的计算方法。
由于高斯核的圆周对称性,使得我们有了简化的方法。我们可以先算一维的高斯核:
![]()
然后再计算即可得到完整高斯核。这样就减少了采样的次数。但是读者们可以自行验算一下
的结果,其每一个元素都比上面的二维高斯核元素要小。这就是误差。由于我们采用的是积分式采样法,采样值大多比直接取点采样要小,而圆周对称性其实是直接采样点才有的特性,所以算出的二维高斯核的元素要比实际值要小。这就是速度与精度的取舍。在实践中,人眼往往不会在意这等细节,所以这样的误差也是可以接受的。
还有一种方法是,在算出一维的高斯核A后,直接用输入图像与其做卷积,得到一个中间图像;再用中间图像与A的转置做卷积。根据卷积的定义,很容易证明这样做的效果与“跟完整的高斯核做卷积”的效果一样。如果原图大小是M×N,那么这种方法能将计算量从减少为
。
在具体的编程手法中,还可以通过一些编程技巧对计算量进行进一步的“压榨”。哪个库的高斯模糊算得更快,甚至可以作为该函数库的水平高低的一个侧面反映。
五、高斯模糊计算时的“切边”问题
其实这并不是高斯模糊特有的问题,一个输入图像与任何的核做卷积的时候都必须处理边缘的问题。边缘的问题的本质是,图像的边缘试图与核做卷积时,核会超出图像边界。如下图所示,红色方框表示高斯核,红色虚线部分表示超出的图像的范围,无法进行卷积。

遇到这种情况一般有3种处理方式:1、丢弃边缘。不能参与卷积的边缘部分将被丢弃。这种做法的缺点是输出图像比输入图像要小“一圈”,尤其是进行多次卷积之后图像将越来越小;2、边缘不参与卷积。边缘的像素保留原值留在输出图像中;3、将图像外的部分设为0,然后参与卷积。三种方法可权衡利弊自行使用。我个人认为第3中种方法较为合适。
六、高斯模糊的一些重要性质
高斯模糊能得到广泛的应用,一个重要原因是因为它具有许多独特的良好性质。除了上面提到的圆周对称性,高斯模糊还有以下几个重要的性质。
性质1:高斯函数的傅立叶变换仍是个高斯函数,也就是说它是个低通滤波器。
可以直观地感受到高斯模糊的低通滤波性。如前所述,高斯模糊实际是做了个加权平均,因此变化剧烈的高频成分,如边缘、条纹、噪点等像素将会变得平滑(即被“压抑”)。而原本比较平滑的地方,做了加权平均一样比较平滑,变化不大(即被“通过”)。σ越小,曲线越尖,高斯核的中心像素的权重也就越大,周围的权重就越小,模糊程度也就越弱。反之,σ越大,则模糊程度越重。
数学上的证明如下。先看一维的情况。
设
则其傅立叶变换为
其中f 表示频域的频率。代入g(x)的表达式,可得
令
则有上式中的积分是著名的高斯积分
计算过程这里不再详述,维基百科中有详细计算过程 跳转到维基百科
因此若使用角频率
,则
可见这是一个标准差为1/σ的高斯函数。σ越大,这个频域的曲线就越尖,高频成分就被抑制得越厉害,图像也就越模糊;反之,σ越小,则图像模糊程度越弱。这与上面在时域的分析结果是一致的。
刚才我说了“时域”,其实这里说“时域”是不准确的,因为并没有“时间”这个变量存在。在图像处理领域,通常称之为“空域”或“空间域”(spatial domain)。而为了强调“频率”的空间性,有时也称之为“空间频率”(spatial frequency)。
对于二维情况,傅立叶变换定义如下
其中u、v可看成分别在x、y方向上的像素变化频率。代入g(x,y)的表达式,可得
同样是个二维高斯函数,即为空间域上的低通滤波器。
性质2:一张图像经过两次高斯模糊,假设两次模糊的标准差分别为和
,则其效果相当于经过一次标准差为
的高斯模糊。写成数学表达式,即为
I(x,y)为输入图像,g为高斯函数,为卷积运算符号。根据卷积的结合律,有
也就是说,这个性质其实说的是如下等式成立。
以下是证明过程。
由傅立叶变换的卷积特性,有
代入上面算得的二维高斯函数的傅立叶变换表达式,可得
这样我们就得到了的傅立叶变换的表达式。再对比
和
的表达式和傅立叶变换表达式,自然可以得出
的表达式应该为
即的标准差为
证明结束。
同样,一维的情况下也有这个结论。
当然,在图像处理这种离散的情况,会发生误差,使得两次标准差分别为和
模糊的结果不能严格等于一次标准差为
的模糊结果。再加上,
、
和
的核很可能大小都不一样,其结果就更不可能相等了。这些误差在图像处理中通常都被忽略,但是我们要知道这些误差的存在。
总结
关于高斯模糊就介绍到这里。这样一个如此常见的概念,细究起来是不是还挺复杂的呢?尤其是以上几个积分,认真计算一下还是得颇费一番工夫的。我们今天轻易地、普遍地使用的工具,其实都是由前人进行了大量的、艰辛的工作所铸就的。向图像分析的开拓者们致敬。
原文:http://www.cnblogs.com/evennl/p/3894438.html