1.1 概率:
A是类别,B是特征。
P(A)是先验概率,表示每种类别分布的概率;
P(B|A)是条件概率,表示在某种类别前提下,某事发生的概率;该条件概率可通过统计而得出,这里需要引入极大似然估计概念,详见后文。
P(A|B)是后验概率,表示某事发生了,并且它属于某一类别的概率,有了这个后验概率,便可对样本进行分类。后验概率越大,说明某事物属于这个类别的可能性越大,便越有理由把它归到这个类别下。
1.2 贝叶斯公式:
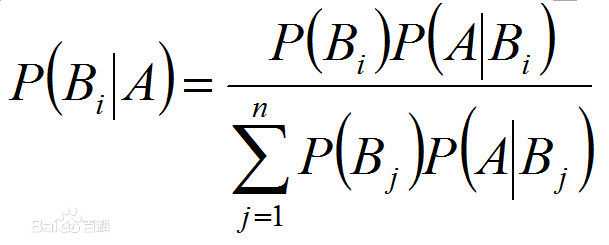
1.3 条件独立性假设:
利用贝叶斯定理求解联合概率P(XY)时,需要计算条件概率P(X|Y)。
在计算P(X|Y)时,朴素贝叶斯做了一个很强的条件独立假设(当Y确定时,X的各个分量取值之间相互独立);
即P(X1=x1,X2=x2,...Xj=xj|Y=yk) = P(X1=x1|Y=yk)*P(X2=x2|Y=yk)*...*P(Xj=xj|Y=yk)。
1.4 朴素贝叶斯法:基于贝叶斯定理与特征条件独立假设的分类方法,是典型的生成学习方法,生成方法由训练数据学习联合概率分布。
1.5 朴素贝叶斯推导:
根据贝叶斯公式及条件独立性假设可得:
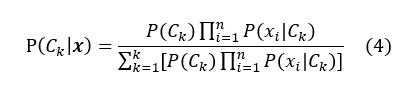
然后将后验概率最大的类作为x的类的输出,因为分母对所有的分类$c_k$都相同,所以:
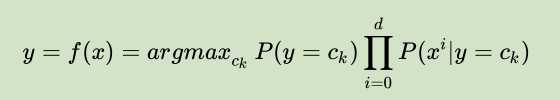
后验概率最大化等价于期望风险最小化。
朴素贝叶斯算法中需要学习$P(y=c_k)$和$P(X^{(j)}=x^{(j)}|Y=x_k)$
2.1 极大似然估计

极大似然估计的缺点

2.2 贝叶斯估计

当$\lambda=0$就是极大似然估计,当$\lambda=1$,这时称为拉普拉斯平滑。
原文:https://www.cnblogs.com/ditingz/p/11777165.html