这篇文章详细地介绍了可持久化线段树、可持久化数组和可持久化并查集,部分图片尺寸过大,建议单击图片放大观看。转载此文章的任何部分均需注明出处。
@
您需要写一个数据结构,维护一个数列 \(a[1...N]\),支持以下操作:
输入 l r k(\(l\leq r,k\leq r-l+1\)),求 \(a[l...r]\) 中第 \(k\) 小的数。
这就是经典的 “静态区间第 k 小” 问题。
可持久化线段树(Persistent Segment Tree)可以很好地解决这个问题。在学习可持久化线段树时,我们首先要了解权值线段树。
权值线段树是一种维护值而非下标的线段树,为了方便理解,有时也被称作 “值域线段树”。
设 \(x\) 是一权值线段树上的一个点,它维护的区间是 \([x.l,x.r]\),数据是 \(x.d\),则它表示的意思是:原数组中,值在区间 \([x.l,x.r]\) 内的数一共有 \(x.d\) 个。
举个例子。有一个数组 \(a[]=\{1,5,3,8\}\),则它的权值线段树是
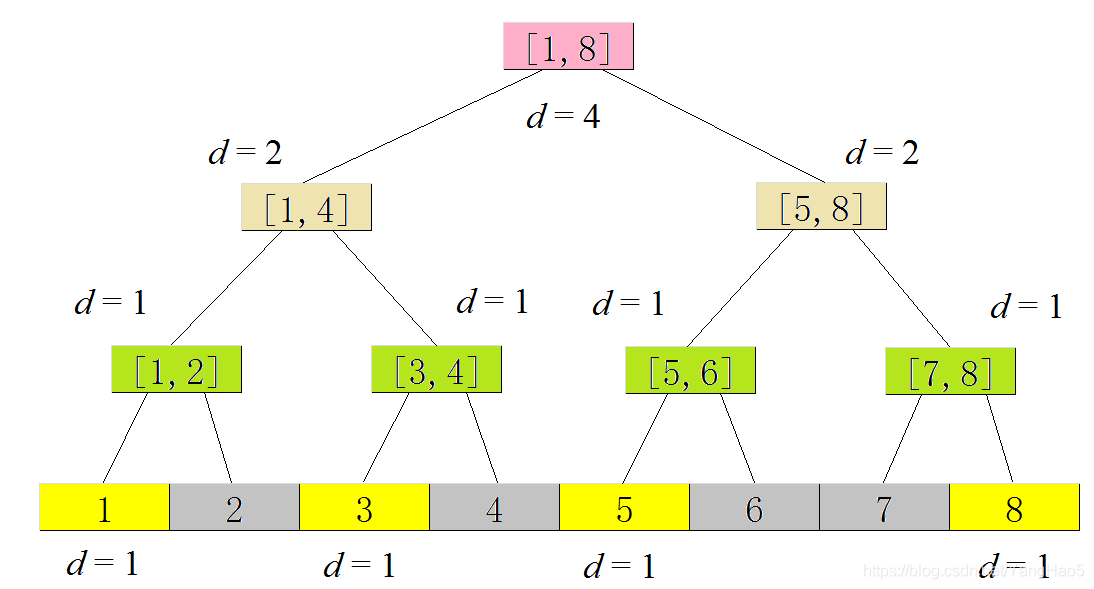
权值线段树可以解决整个区间的查询问题。换句话说,当 \(l=1,r=N\) 时,我们就可以用权值线段树求解了。
那如果 \(l\neq1\) 或 \(r\neq N\),我们又该怎么办呢?
一种很显然的想法就是,我建 \(\frac {N(N+1)}2\) 棵权值线段树,也就是说,\(\forall 1\leq l\leq r\leq N\),我都建一棵权值线段树维护 \(a[l...r]\)。这样做的话空间复杂度是 \(T(N^3)\),不能接受。而且这样做的话,光是建树就会导致超时。
不难发现,权值线段树是可加减的。也就是说,我可以只开 \(N\) 棵权值线段树,第 \(i\) 棵维护 \(a[1...i]\) 范围的数(这里用了前缀和思想)。如果查询 \([l,r]\) 区间,就用第 \(r\) 棵树减去第 \(l-1\) 棵树即可。
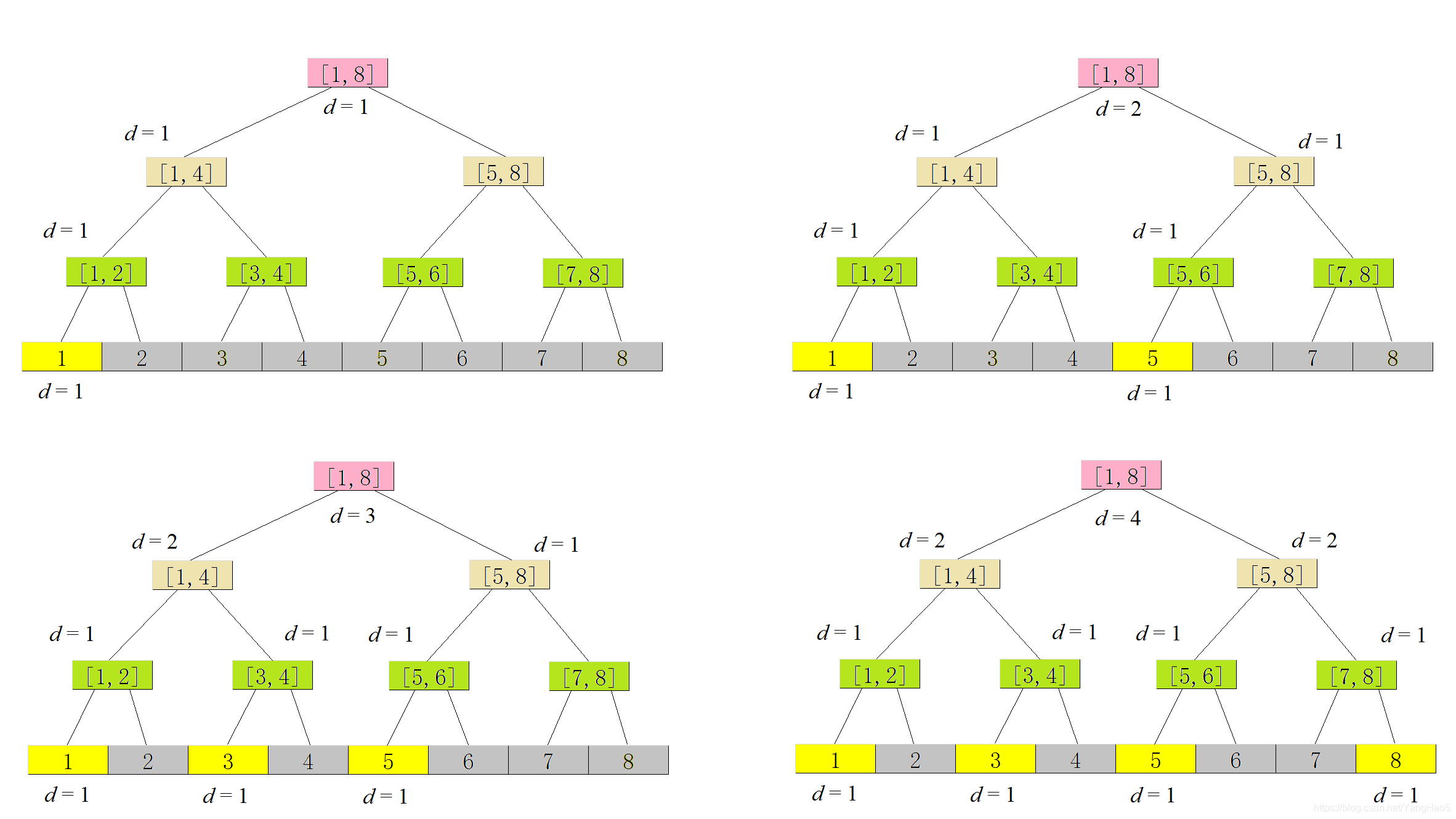
时间复杂度 \(O(N^2+M\log N)\),空间复杂度 \(T(N^2)\),仍然不够优秀。
观察上面的四棵树。不难发现,第 \(i\) 棵树与第 \(i-1\) 棵树只有一条链不一样,其余部分完全相同。那么,我们能不能在这里做点文章,压缩时间、空间复杂度呢?
答案是肯定的。我们每次建树时,不需要新建一棵完整的树,只需要在原来的树上加一条链就行了。
还是以 \(a[]=\{1,5,3,8\}\) 为例,画出可持久化线段树:
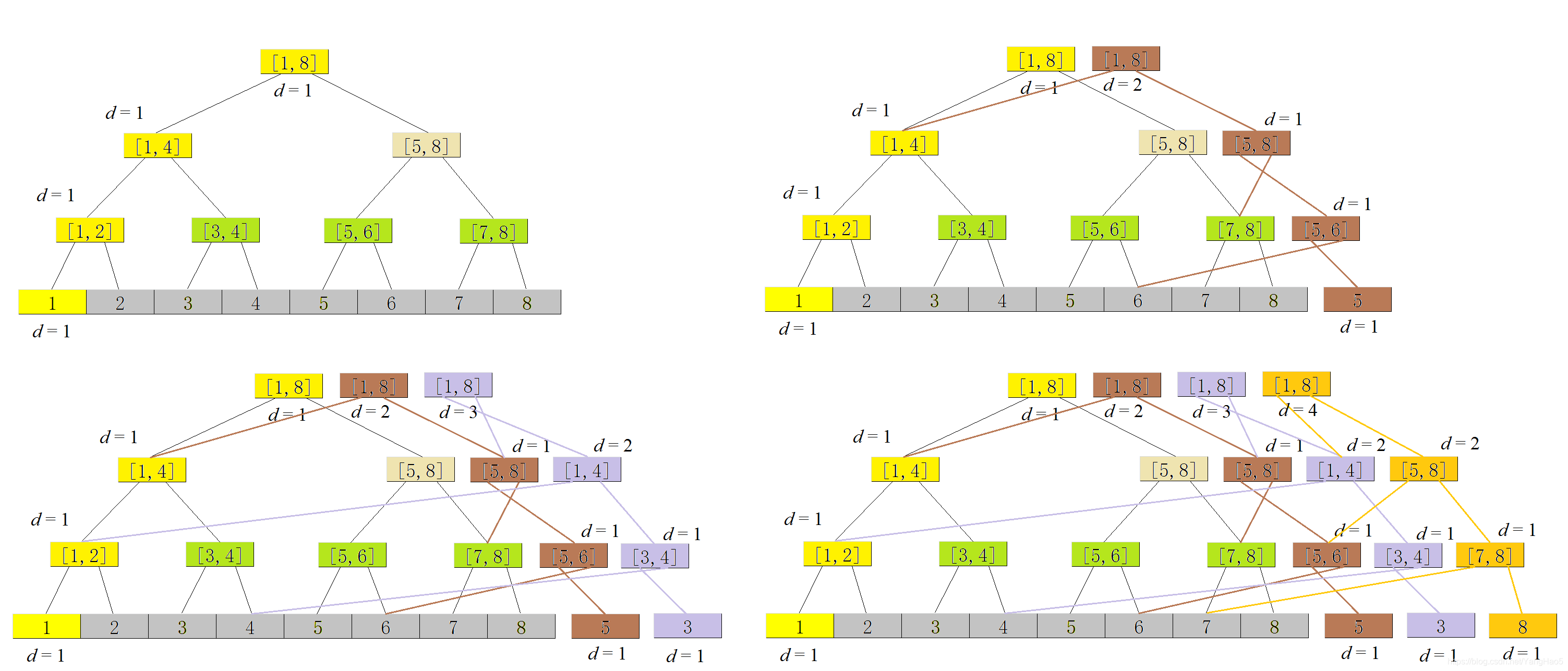
最后一棵就是最终形态的可持久化线段树了。时间复杂度 \(O(N\log N)\),空间复杂度 \(T(N\log N)\)。
至此,可持久化线段树的基本内容已经讲解完毕了,我们现在已经可以解决文首提出的问题了。
静态区间第 k 小问题 如题,给定 \(N\) 个整数构成的序列,将对于指定的闭区间查询其区间内的第 \(K\) 小值。
解 将两棵可持久化线段树相减(容易想到,如果将第 \(r\) 棵树减去第 \(l-1\) 棵树,那结果就是 \([l,r]\) 区间的权值线段树了)。从根节点开始,往下遍历,若左子树维护区间的数的个数 \(d<K\),则走向左儿子,否则走向右儿子;重复以上操作,直到走到叶子节点,该节点的下标即为答案。
参考代码
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=200010;
int n,m;
struct index{
int x,y;
friend bool operator<(const index a,const index b){
return a.y<b.y;
}
}a[MAXN];
int b[MAXN];
int mp[MAXN];
int sx,sy,sd;
inline int read(){
int x=0; char c;
do c=getchar(); while(c<'0'||c>'9');
while(c>='0'&&c<='9')
x=x*10+c-48,c=getchar();
return x;
}
struct PreSegTree{
struct index{
int l,r,ls,rs,d;
index(){
l=r=ls=rs=d=0;
}
}e[MAXN*40];
int len;
int root[MAXN];
PreSegTree(){
len=0;root[0]=1;
}
void buildtree(int l,int r){
int me=++len;
e[me].l=l;e[me].r=r;
if(l==r) return;
int mid=(l+r)/2;
e[me].ls=len+1;buildtree(l,mid);
e[me].rs=len+1;buildtree(mid+1,r);
}
void grow(int rt,int x){
int l=e[rt].l,r=e[rt].r,me=++len;
e[me].l=l;e[me].r=r;
if(l==r){
e[me].d=e[rt].d+1;
return;
}
int mid=(l+r)/2;
if(x<=mid){
e[me].ls=len+1;e[me].rs=e[rt].rs;
grow(e[rt].ls,x);
}else{
e[me].ls=e[rt].ls;e[me].rs=len+1;
grow(e[rt].rs,x);
}
e[me].d=e[e[me].ls].d+e[e[me].rs].d;
}
void insert(int x,int d){
root[x]=len+1;
grow(root[x-1],d);
}
int query(int rootl,int rootr,int k){
int LS=e[rootl].ls,RS=e[rootr].ls;
int D=e[RS].d-e[LS].d;
if(e[rootl].l==e[rootl].r) return e[rootl].r;
if(k<=D) return query(LS,RS,k);
else return query(e[rootl].rs,e[rootr].rs,k-D);
}
}T;
int main(){
n=read();m=read();
T.buildtree(1,n);
for(int i=1;i<=n;++i)
a[i].x=i,a[i].y=read();
sort(a+1,a+n+1);
int tmp=0,last=-0x3f3f3f3f;
for(int i=1;i<=n;++i){
if(a[i].y!=last){
++tmp;
mp[tmp]=a[i].y;
}
b[a[i].x]=tmp;
last=a[i].y;
}
for(int i=1;i<=n;++i)
T.insert(i,b[i]);
for(int i=1;i<=m;++i){
sx=read();sy=read();sd=read();
printf("%d\n",mp[T.query(T.root[sx-1],T.root[sy],sd)]);
}
}你需要维护这样的一个长度为 \(N\) 的数组,支持如下几种操作:
此外,每进行一次操作(对于操作 2,即为生成一个完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从 1 开始编号,版本 0 表示初始状态数组)
算法 1 我们可以考虑对每一个版本开一个数组,这就是最暴力的打法了。
算法 2 高级一点,我们可以考虑对每一个版本建一棵线段树,查询时在线段树上查询,这样的效率还不如一个暴力数组。
算法 3 考虑用可持久化线段树维护每个位置上的值,也就是说每修改一次就加一条链。查询操作与上文类似,在此不再赘述。
(未完待续)
原文:https://www.cnblogs.com/yhmaster/p/11780526.html