无约束优化方法

概述

前言：无约束优化问题是实际问题中会碰到的问题。在解决约束优化问题的过程中会用到无约束优化问题的解法或思想。古典极值理论中，令一阶导为 0 ，要求二阶可微，然后判断海塞矩阵为正定才能求极小点，有理论意义而没有使用价值，实际中的多元函数很多不可微或不可求二阶导。但古典极值理论是无约束优化方法发展的基础。

无约束优化的数学模型：

\[ min\ f(x)\quad x\in R^n \]

目前已研究出很多无约束优化方法，它们的主要不同点在于构造搜索方向上的差别。

1. 解析法

   直接应用目标函数极值条件来确定极值点。把求解目标函数极值的问题变成求解 \(\bigtriangledown f(x)=0\)，一般求解比较困难，需要采用数值方法求解。与其用数值方法求解这个非线性方程组，还不如直接用数值法求解无约束极值问题。

2. 数值法

   数值法采用数学规划的思想，从起始点 \(x_k\) 开始沿搜索方向 \(d^0\) 进行搜索，确定最优步长 \(\alpha_k\) 使得函数值沿搜索方向下降最大。形成迭代的下降算法
   \[ x^{k+1}=x^k+\alpha_kd^k \]
   其中 \(d^k\) 是第 \(k+1\) 次搜索或迭代方向，称为搜索方向 (迭代方向)。

各种无约束优化方法的主要区别就在于确定搜索方向的方法不同。搜索方向的构成问题是无约束优化方法的关键。

无约束优化方法分类：

根据构成搜索方向 \(d^k\) 所使用的信息性质，分为

1. 利用目标函数的一阶或二阶导构造搜索方向的无约束优化方法 (间接法)。
   • 最速下降法
   • 牛顿法
   • 共轭方向法
   • 共轭梯度法
   • 变尺度法
2. 只用目标函数值的信息构造搜索方向的无约束优化方法 (直接法)。
   • 坐标轮换法
   • 鲍威尔方法
   • 单型替换法

最速下降法

最速下降法是一个古老的求解极值的方法，于 \(1847\) 年由柯西提出。

主要就是取负梯度方向为搜索方向。所以最速下降法又称 “梯度法”。

迭代算法为：

1. 初始点 \(x^0\)，\(k=0\)，迭代阈值 \(\varepsilon\)

2. 求 \(\bigtriangledown f(x^k)\)，如果 \(||\bigtriangledown f(x^k)||\le \varepsilon\)，输出 \(x^k\) 为最小值点，算法结束。否则继续。

3. 确定搜索方向 \(d_k=-\bigtriangledown f(x^k)\)

4. 确定一维搜索的最佳步长 \(\alpha_k\)
   \[ f(x^{k+1})=f[x^k-\alpha_k\bigtriangledown f(x^k)]=\min\limits _a f[x^k-\alpha\bigtriangledown f(x^k)]=\min\limits _a \phi(\alpha) \]

   \[ \phi'(\alpha)=-\{\bigtriangledown f[x^k-\alpha_k\bigtriangledown f(x^k)]\}^T\bigtriangledown f(x^k)=0\\ \Rightarrow [\bigtriangledown f(x^{k+1})]^T\bigtriangledown f(x^k)=0 \]

   即相邻两迭代点上的函数梯度相互垂直，即相邻两个搜索方向互相垂直。

   搜索路线呈“之”字锯齿形。

在接近极小点的位置，由于“之”字路线使得每次迭代行进的距离缩短，收敛速度减慢。主要是因为梯度是函数的局部性质，从整体看还是走了弯路，函数下降并不如人意。

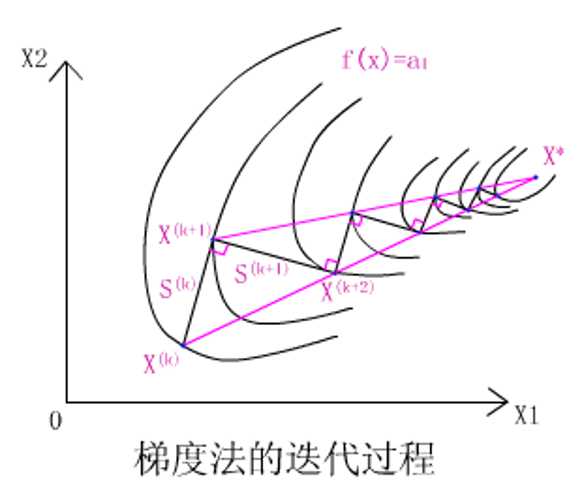
小结：

1. 理论明确，程序简单，对初始点要求不严格
2. 因为梯度是函数的局部性质，所以整体收敛速度不快
3. 搜索路线呈锯齿状，在远离极小点时逼近速度较快，接近极小点时速度较慢。
4. 收敛速度与目标函数性质密切相关 。目标函数的等值线形成的椭圆簇越扁，迭代次数越多，搜索难以到达极小点；而同心圆，或椭圆簇对称轴，则一次搜索即可到达。(圆的切线垂直方向经过圆心，椭圆切线垂直方向不经过，除非在对称轴上的点)

最速下降法可以使目标函数在头几步下降特别快，所以可以与其他无约束优化方法配合使用。先最速下降求得较优初始点，再用其他收敛快的方法继续寻找极小点。

牛顿型方法

牛顿法

基本思想：用二次函数近似原目标函数，使用二次函数的极小点作为下一个迭代点。

泰勒展开：
\[ f(x)\approx \phi(x)=f(x^k)+\bigtriangledown f(x^k)^T(x-x^k)+\frac{1}{2}(x-x^k)^T\bigtriangledown^2 f(x^k)(x-x^k) \]
设 \(x^{k+1}\) 为 \(\phi(x)\) 极小点，则 \(\bigtriangledown \phi(x^{k+1})=0\)
\[ \bigtriangledown f(x^k)+\bigtriangledown^2 f(x^k)(x^{k+1}-x^k)=0\\\Rightarrow x^{k+1}=x^k-[\bigtriangledown^2 f(x^k)]^{-1}\bigtriangledown f(x^k) \]
牛顿法能使二次型函数在有限次迭代内达到极小点，是二次收敛的。(对于二次函数，展开到二次项的泰勒展开式就是其本身，海塞矩阵是一个常数阵，一步找到极小点)

牛顿法纯粹基于极值的计算来确定极值点，没有包含下降方向搜索的思想，所以对于非二次函数，有时迭代后反而使函数值上升。

阻尼牛顿法

把 \(d^k=-[\bigtriangledown^2 f(x^k)]^{-1}\bigtriangledown f(x^k)\) 看作一个搜索方向，并称为 “牛顿方向”，再引入搜索方向里 “步长的” 概念。
\[ f(x^{k+1})=f(x^k+\alpha_kd^k)=\min\limits_\alpha f(x^k+\alpha_kd^k) \]

• \(\alpha_k\) 是沿牛顿方向进行一维搜索的最佳步长，叫做 “阻尼因子”
• 原始牛顿法就是阻尼因子恒为1的情况

阻尼牛顿法每次都在牛顿方向上一维搜索，避免了迭代后数值上升的现象，又保留了牛顿法二次收敛的特性。

但是牛顿型方法每次都要计算海塞矩阵，再对海塞矩阵求逆，计算量巨大。条件苛刻，二次不可微的 \(f(x)\) 也不适用，若海塞矩阵是奇异矩阵不能求逆矩阵，也进行不下去，为了保证牛顿方向是下降方向，海塞矩阵的逆矩阵还必须正定。

共轭方向及共轭方向法

共轭梯度法

变尺度法

坐标轮换法

鲍威尔方法

单型替换法

[最优化理论与技术]无约束优化方法

原文：https://www.cnblogs.com/ColleenHe/p/11782538.html