洛谷P2607题解

想要深入学习树形DP，请点击我的博客。

本题的DP模型同 P1352 没有上司的舞会。本题的难点在于如何把基环树DP转化为普通的树上DP。

考虑断边和换根。先找到其中的一个环，在上面随意取两个点， 断开这两个点的边，使其变为一棵普通树。以其中的一点为树根做树形DP，再以另一点为树根再做一次树形DP，因为相邻的两点不能同时选，所以最后统计一下 \(f(i)(0)\) 与 \(g(j)(0)\) 的最大值即可。

定义 \(f(i)(0/1)\) 为第一次树形DP的 \(i\) 点的最优解，\(g(i)(0/1)\) 为第二次树形DP的 \(i\) 点的最优解。$\text{Ans} $ 为一次基环树DP的答案。\(\text{E}_\text{Circle}\) 为基环树的环上的点的集合。

故一次基环树DP的答案为：
\[ \text{Ans}=\max\{f(i)(0),g(j)(0)\} \]

\[ (i,j\in \text{E}_\text{Circle},i\neq j) \]

下图为洛谷秋令营的课件讲解:

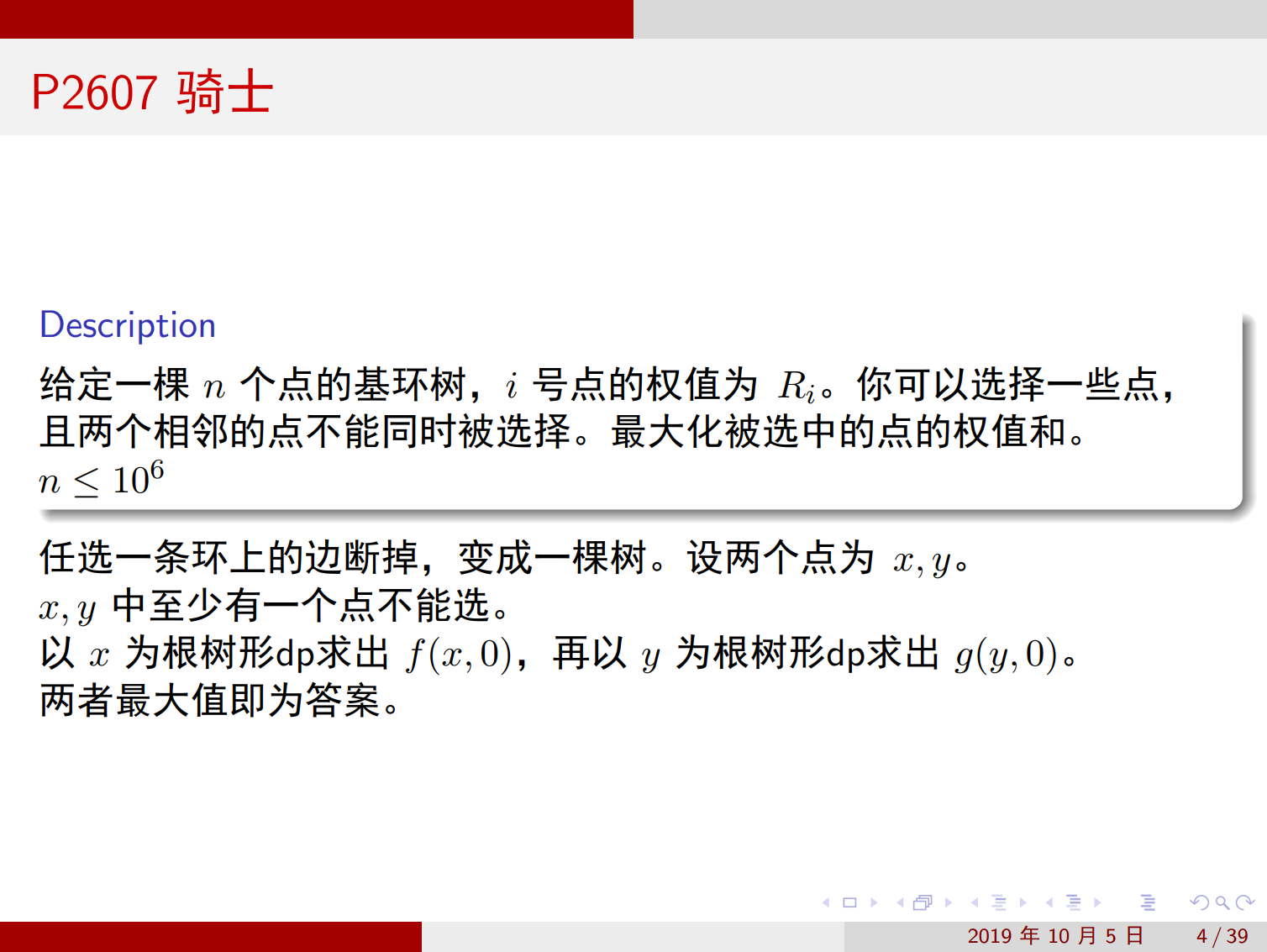
关键代码如下：

void covertree(int fr)//寻找基环树
{
 used[fr]=1;
 for(int i=head[fr];i;i=e[i].next)
 {
     int to=e[i].to;
     if(used[to]==0)
     {
         covertree(to);
     }
 }
}


void findcir(int fr,int fa)//寻找基环树中的环
{
 if(flag) return ;
 vis[fr]=1;
 for(int i=head[fr];i;i=e[i].next)
 {
     int to=e[i].to;
     if(vis[to]==0)
     {
         findcir(to,fr);
     }else if(to!=fa)
     {
         fri=fr;//第一个点
         toi=to;//第二个点
         E=i;//边的编号
         flag=1;
         return ;
     }
 }
}


void DPf(int fr)//以其中的一点为树根做树形DP
{
 visf[fr]=1;
 f[fr][1]=crit[fr];
 for(int i=head[fr];i;i=e[i].next)
 {
     int to=e[i].to;
     if(visf[to]==0&&(i^1)!=E)//保证不会选到第一个点和第二个点，相当于断边
     {
         DPf(to);
         f[fr][0]+=max(f[to][0],f[to][1]);
         f[fr][1]+=f[to][0];
     }
 }
}


void DPg(int fr)//再以另一点为树根再做一次树形DP
{
 visg[fr]=1;
 g[fr][1]=crit[fr];
 for(int i=head[fr];i;i=e[i].next)
 {
     int to=e[i].to;
     if(visg[to]==0&&(i^1)!=E)
     {
         DPg(to);
         g[fr][0]+=max(g[to][0],g[to][1]);
         g[fr][1]+=g[to][0];
     }
 }
}

for(int i=1;i<=n;i++)//调用+统计答案
{
 if(used[i]==1) continue;
 covertree(i);
 flag=0;
 findcir(i,-1);
 DPf(fri);
 DPg(toi);
 ans+=max(f[fri][0],g[toi][0]);
}

特别注意：

• 本题是基环树森林，而不是单棵基环树，故要反复寻找覆盖基环树，最后将所有答案加起来。

• 因为要断边，所以前向星计数器 ei一定要初始化为 1。

  • 用多个数组标记（used[],vis[],visf[],visg[]）。
  • 一定要注意 f,g 和 fr,to，不要手快打错了。

洛谷P2607题解

原文：https://www.cnblogs.com/nth-element/p/11785016.html