概述:通过将一棵树上的点分为轻重链,来降低复杂度,此时lca查询复杂度为\(O(logn)\),支持在线。
重儿子:一个有根树的一个点 子树最大的儿子
轻儿子:其它的儿子
重链:由重儿子连接成的链
轻链:其它的所有链
下图是一棵剖好的树
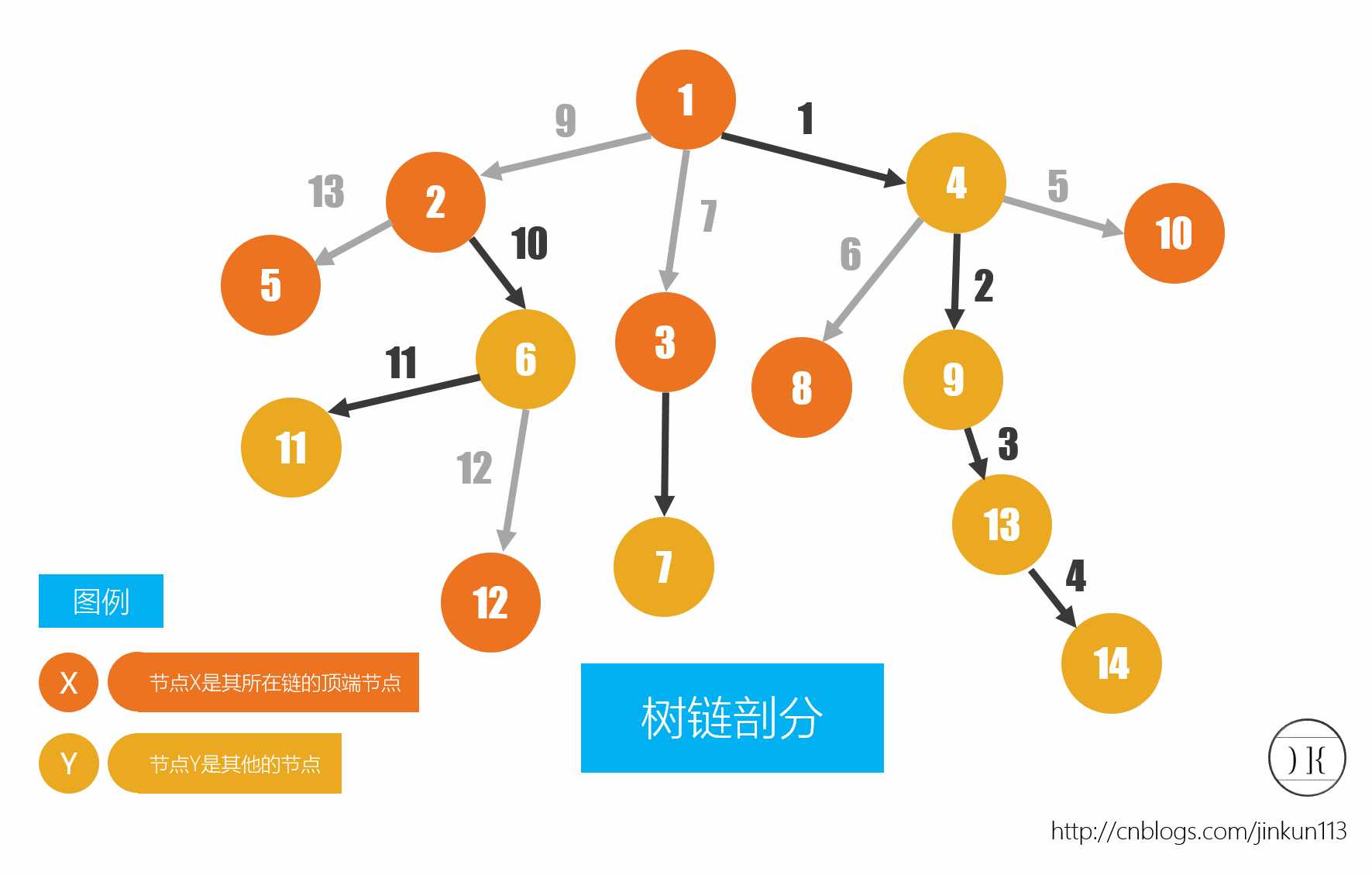
图片来自于[知识点]树链剖分
树剖本体其实只有两个dfs
第一个dfs处理每个子树的大小,重儿子一类的信息
第二个dfs处理剖出的链的信息
void dfs1(int x) {
int mx = -1;
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if(v == fa[x]) continue;
dep[v] = dep[x] + 1;//处理深度
fa[v] = x;//父节点
siz[x]++;//大小
dfs1(v);
siz[x] += siz[v];//回溯
if(siz[v] > mx) {//保留重儿子
mx = siz[v];
son[x] = v;
}
}
}void dfs2(int x, int tp) {
top[x] = tp;//链顶
if(son[x] != 0) {
dfs2(son[x], tp);//优先搜索重儿子,让重儿子先成链
}
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if(v == son[x] || v == fa[x]) continue;
dfs2(v, v);//处理其它节点
}
}我们手上现在有剖好的链
我们一次上跳就可以跳一条链的长度,所以时间复杂度大大降低
int getlca(int x, int y) {
int f1 = top[x];//链顶
int f2 = top[y];
while(f1 != f2) {
if(dep[f1] > dep[f2]) {//始终让x在上方
swap(f1, f2);
swap(x, y);
}
y = fa[f2];//将y向上跳f2的父节点即是别的链的一部分
f2 = top[y];//更新链顶
}
if(dep[x] < dep[y]) {//当两个链顶在一起时,说明两个点在一条链上
return x;//此时返回深度较浅的点
}
else return y;
}描述
已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
既然想要处理链上信息
我们就想要处理的信息连续
dfs序帮我们解决了这个问题
按dfs遍历到的顺序保存下节点即可
void dfs2(int x, int tp) {
top[x] = tp;
dfn[x] = ++tot;//保存dfs序
wt[tot] = val[x];//保存节点值
if(son[x]) {
dfs2(son[x], tp);
}
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if(v == fa[x] || v == son[x]) continue;
dfs2(v, v);
}
}接下来就可以带入数据结构解决问题
考虑线段树
update及query为普通线段树的处理
void update_lst(int x, int y, int z) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) {
swap(x, y);
}
update(1, 1, n, dfn[top[x]], dfn[x], z);//不断对较低的点所在的链处理,
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
update(1, 1, n, dfn[x], dfn[y], z);//当两点在一条链上时
}和update_lst()差不多
int query_lst(int x, int y) {
int ret = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) {
swap(x, y);
}
ret = (ret + query(1, 1, n, dfn[top[x]], dfn[x])) % p;
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
ret = (ret + query(1, 1, n, dfn[x], dfn[y])) % p;
return ret;
}因为dfs序的处理现在每条链的下标都是连续的,长度就是siz[x]
void update_tre(int x, int z) {
update(1, 1, n, dfn[x], dfn[x] + siz[x], z);
}int query_tre(int x) {
return query(1, 1, n, dfn[x], dfn[x] + siz[x]);
}#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <cmath>
#define MAXN 100007
using namespace std;
int n, m, r, p, tot;
int val[MAXN];
int head[MAXN], cnt;
struct node {
int v, next;
}e[MAXN << 1];
void add(int u, int v) {
e[++cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt;
}
int son[MAXN], fa[MAXN], top[MAXN], siz[MAXN];
int dfn[MAXN], dep[MAXN], wt[MAXN];
void dfs1(int x) {
int mx = -1;
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if(v == fa[x]) continue;
dep[v] = dep[x] + 1;
fa[v] = x;
siz[x]++;
dfs1(v);
siz[x] += siz[v];
if(siz[v] > mx) {
mx = siz[v];
son[x] = v;
}
}
}
void dfs2(int x, int tp) {
top[x] = tp;
dfn[x] = ++tot;
wt[tot] = val[x];
if(son[x]) {
dfs2(son[x], tp);
}
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if(v == fa[x] || v == son[x]) continue;
dfs2(v, v);
}
}
int tree[MAXN << 3], lazy[MAXN << 3];
void pushup(int o) {
tree[o] = tree[o << 1] + tree[o << 1 | 1];
tree[o] %= p;
}
void pushdown(int o, int l, int r) {
if(!lazy[o]) return ;
int mid = (l + r) >> 1;
tree[o << 1] = (tree[o << 1] + lazy[o] * (mid - l + 1)) % p;
tree[o << 1 | 1] = (tree[o << 1 | 1] + lazy[o] * (r - mid)) % p;
lazy[o << 1] = (lazy[o << 1] + lazy[o]) % p;
lazy[o << 1 | 1] = (lazy[o << 1 | 1] + lazy[o]) % p;
lazy[o] = 0;
return ;
}
void build(int o, int l, int r) {
if(l == r){
tree[o] = wt[l];
return ;
}
int mid = (l + r) >> 1;
build(o << 1, l, mid);
build(o << 1 | 1, mid + 1, r);
pushup(o);
}
void update(int o, int l, int r, int ql, int qr, int val) {
if(ql <= l && qr >= r) {
tree[o] = (tree[o] + val * (r - l + 1)) % p;
lazy[o] = (lazy[o] + val) % p;
return ;
}
pushdown(o, l, r);
int mid = (l + r) >> 1;
if(ql <= mid) update(o << 1, l, mid, ql, qr, val);
if(qr > mid) update(o << 1| 1, mid + 1, r, ql, qr, val);
pushup(o);
}
int query(int o, int l, int r, int ql, int qr) {
if(ql <= l && qr >= r) {
return tree[o];
}
pushdown(o, l, r);
int mid = (l + r) >> 1, ret = 0;
if(ql <= mid) ret = (ret + query(o << 1, l, mid, ql, qr)) % p;
if(qr > mid) ret = (ret + query(o << 1 | 1, mid + 1, r, ql, qr)) % p;
return ret % p;
}
void update_lst(int x, int y, int z) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) {
swap(x, y);
}
update(1, 1, n, dfn[top[x]], dfn[x], z);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
update(1, 1, n, dfn[x], dfn[y], z);
}
int query_lst(int x, int y) {
int ret = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) {
swap(x, y);
}
ret = (ret + query(1, 1, n, dfn[top[x]], dfn[x])) % p;
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
ret = (ret + query(1, 1, n, dfn[x], dfn[y])) % p;
return ret;
}
void update_tre(int x, int z) {
update(1, 1, n, dfn[x], dfn[x] + siz[x], z);
}
int query_tre(int x) {
return query(1, 1, n, dfn[x], dfn[x] + siz[x]);
}
int main() {
scanf("%d%d%d%d", &n, &m, &r, &p);
for(int i = 1; i <= n; i++) {
scanf("%d", &val[i]);
}
for(int i = 1; i < n; i++) {
int u, v;
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
dfs1(r);
dfs2(r, r);
build(1, 1, n);
for(int i = 1; i <= m; i++) {
int op, x, y, z;
scanf("%d", &op);
if(op == 1) {
scanf("%d%d%d", &x, &y, &z);
update_lst(x, y, z);
}
if(op == 2) {
scanf("%d%d", &x, &y);
printf("%d\n", query_lst(x, y) % p);
}
if(op == 3) {
scanf("%d%d", &x, &z);
update_tre(x, z);
}
if(op == 4) {
scanf("%d", &x);
printf("%d\n", query_tre(x) % p);
}
}
}原文:https://www.cnblogs.com/wyswyz/p/11787835.html