决策树是一种基本的分类与回归方法，其树模型是描述对实例进行分类的树状结构。
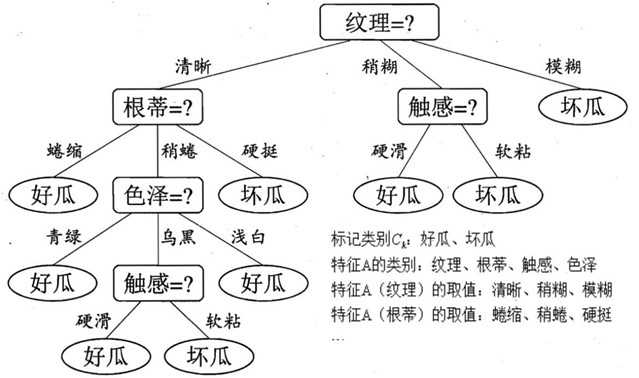
图1-1 摘自《机器学习》的西瓜分类决策树
假设给定训练数据集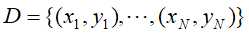
，其中
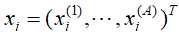为输入实例，A为特征类别数，
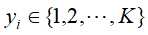为标记类（在下面用
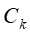表示所标记类别，
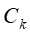为数据集D根据标记类别的不同所划分的子集
）。
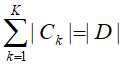设特征A（某一特征类别）有n个不同的取值，数据集D根据特征A（某一特征类别）的取值将其划分为n个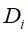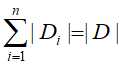子集
，
。记子集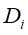
中属于某标记类别
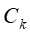的样本集合为
，
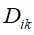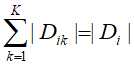。那么决策树则根据训练数据集构建模型，使其能够对实例进行正确分类。
决策树的学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪。
?
1. 特征选择
特征选择的关键在于选取对数据具有分类能力的特征，通常采用的准则为信息增益或信息增益比。
在引入信息增益和信息增益比之前，先介绍熵（entropy）和条件熵。
熵度量了随机变量的不确定性，设有一离散型的随机变量X，其概率分布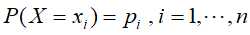为
，则其熵为
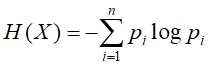
条件熵，同样先假设有一随机变量（X，Y），其联合概率分布为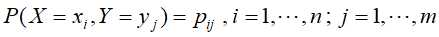
，则条件熵表示在已知随机变量X的条件下随机变量Y的不确定性，定义为
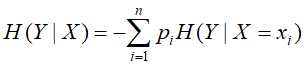
明确了熵和条件熵的定义后，将求信息增益则表示，在得知特征X的信息后，类Y信息的不确定性减少程度。
特征A对训练数据集D的信息增益g（D，A）定义为集合D的熵H（D）与特征A给定条件下D的条件熵H（D|A）之差，即
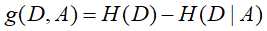
那么信息增益准则的特征选取方法为：对训练数据集D，计算每一个特征的信息增益，然后选取信息增益最大的分类特征。
?
信息增益比则是信息增益g（D，A）与训练数据集D关于特征A的值的熵之比，即
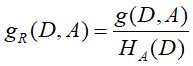
其中，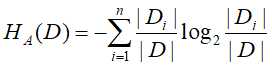
，n是特征A的取值个数，信息增益比解决了信息增益偏向于选择取值较多的特征问题。
?
2. 决策树的生成
决策树的生成根据特征选取准则的不同，有两种生成方式：ID3算法和C4.5算法。
ID3算法：
输入：训练数据集合D，特征A集合阈值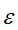
；
输出：决策树T
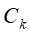，则t为单结点树，并将
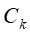作为该结点的标记类别，返回T；
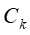作为该结点的标记类别，返回T；
；
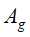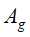的信息增益小于阈值
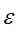，则t为单结点树，将子集D中实例树最大类别
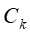作为该结点的标记类别，返回T；
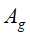的信息增益不小于阈值
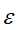，对
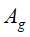的每一可能取值
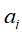，将子集D划分若干非空子集
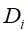，对应构成若干个子结点，对第i个子结点，以
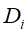为训练集，以
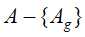为特征集，递归地调用（1）至（5）步骤，得到子树
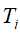，返回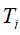
。
?
C4.5算法：
输入：训练数据集合D，特征A集合阈值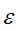
；
输出：决策树T
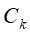，则t为单结点树，并将
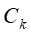作为该结点的标记类别，返回T；
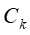作为该结点的标记类别，返回T；
；
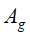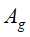的信息增益比小于阈值
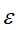，则t为单结点树，将子集D中实例树最大类别
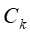作为该结点的标记类别，返回T；
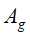的信息增益比不小于阈值
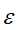，对
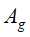的每一可能取值
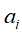，将子集D划分若干非空子集
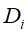，对应构成若干个子结点，对第i个子结点，以
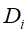为训练集，以
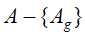为特征集，递归地调用（1）至（5）步骤，得到子树
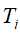，返回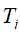
。
?
ID3和C4.5的算法步骤相似，区别在于ID3计算信息增益而C4.5计算信息增益比。
?
3. 决策树的剪枝
决策树的剪枝通常用极小化决策树整体的损失函数或代价函数实现。
设树T的叶结点树为|T|，t是树T的叶结点，该叶结点有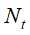
个样本点，其中属于
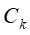类别的样本点有
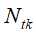个，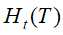
为叶结点t上的熵，
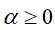为参数，则决策树的损失函数可以定义为
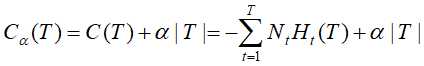
其中，熵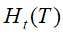
为
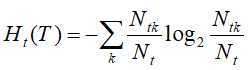
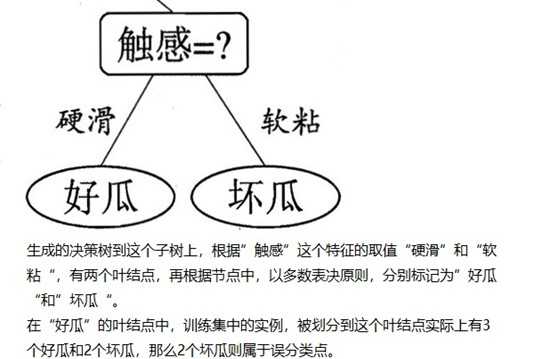
图3-1 树结点参与损失函数的计算
决策树的剪枝算法：
输入：生成算法产生的整个树T，参数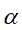
；
输出：修剪后的子树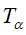
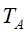和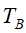
，其对应的损失函数分别为
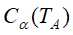和
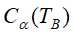，如果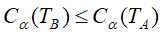
，则进行剪枝，将其父结点变为新的叶结点；
。
?
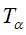剪枝算法可以结合到决策树的生成算法中，这样可以减少模型生成所消耗的时间。
?
?
?
?
原文：https://www.cnblogs.com/lincz/p/11789832.html