最大熵模型(maximum entropy model)是由最大熵原理(概率模型在满足约束条件下,其他不确定的部分是"等可能"的)推导实现。
比如,有随机变量X有5个取值{A,B,C,D,E},在P(A)+P(B)+P(C)+P(D)+P(E)=1而没有其他限制的条件下,则估计X的各个取值都是等可能的1/5;假设有限制条件如下:P(A)+P(B)=3/10,那么估计X的取值则会认为A、B是等可能的,C、D、E三者又是等可能的,最终我们将会得到这样的估计概率分布:P(A)=P(B)=3/20,P(C)=P(D)=P(E)=7/30。
定义:
有一训练数据集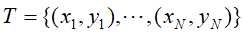 ,
,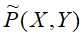 和
和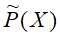 为经验分布,用特征函数表示输入x和输出y之间的某一事实。
为经验分布,用特征函数表示输入x和输出y之间的某一事实。

特征函数f(x,y)关于经验分布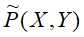 的期望值,
的期望值,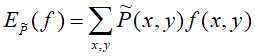
特征函数f(x,y)关于模型P(X|Y)与经验分布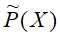 的期望,
的期望,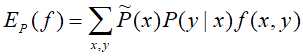
如果模型能获取训练数据中信息,就假设上述的两个期望相等。
假设满足所有约束条件的模型集合为
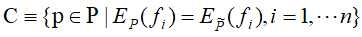
定于在条件概率分布P(X|Y)上的条件熵为
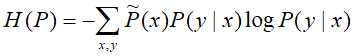
则模型集合C中条件熵H(P)最大的模型称为最大熵模型。
学习:
最大熵模型的学习等价约束最优化问题:
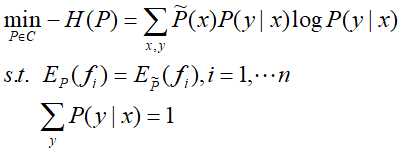
将约束最优化的问题转换为无约束最优化的对偶问题。
首先,引入拉格朗日乘子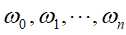 ,对应的拉格朗日函数
,对应的拉格朗日函数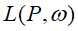 :
:
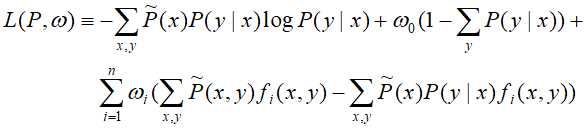
那么最优化的原始问题为: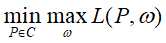
因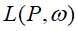 是凸函数,故最优化原始问题等价于对偶问题:
是凸函数,故最优化原始问题等价于对偶问题: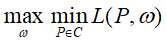 ,那么最大熵模型学习即归结为对偶函数极大化
,那么最大熵模型学习即归结为对偶函数极大化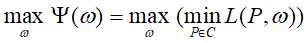 。
。
在这,先求解对偶函数内部的极小化可得:
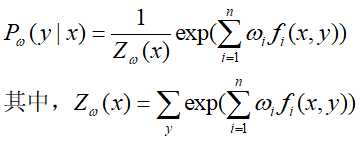
将上述结果带入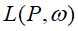 得:
得: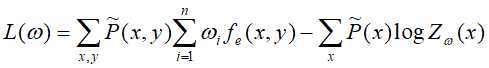
最终,再利用IIS或是牛顿法求解最优参数和对应的最优模型。
改进的迭代尺度算法IIS:
输入:特征函数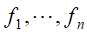 ;经验分布
;经验分布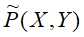 和模型
和模型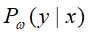 、
、
输出:最优参数值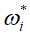 ;最优模型
;最优模型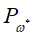
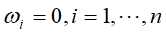
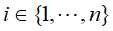
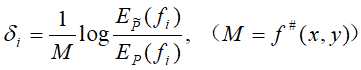 是方程
是方程
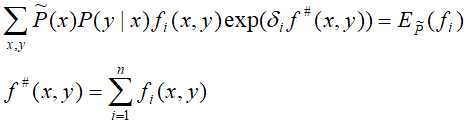
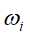 收敛,则重复步骤(2)。
收敛,则重复步骤(2)。原文:https://www.cnblogs.com/lincz/p/11789855.html