（某种）数列问题

【题目描述】

　　给定一个长度为 n 的整数序列，可能存在负数，从中找到 3 个无交集的连续 子数列使其和最大。一个元素不能被编入多个序列而且一定要拿出 3 个序列。 简单滴说就是： 给定一个数列，从中找到 3 个无交集的连续子数列使其和最大。

【输入文件】

　　第一行一个数 n，表示数列长度。

　　接下来有 n 行，每行一个数，第 i 行为第 i 个数。

【输出文件】

　　仅有一个数，表示最大和。

【样例输入】

　　 10 -1 2 3 -4 0 1 -6 -1 1 -2

【样例输出】

　　 7

【样例说明】

　　 第一个序列取 2，3。

　　 第二个序列取 0，1。

　　 第三个序列取 1。

【数据范围】

　　 对于 30%的数据，n<=200。 对于 60%的数据，n<=2000。 对于 100%的数据 n<=1000000。 答案不超过 maxlongint。

　　 模拟赛的题目，一开始知道是动规，但是完全懵逼，上网查了之后才发现是【某种数列问题】（题目名，真的连样例都没改，可以自己上网查）。

　　  核心思路

　　   设定一个数组f，约定f[i][j][k](0<=i<=n,0<=j<=3,k=1或0)为在第i个位置时，把前面i-1个数分成j组，当k=1时取第i个数，k=0则不取。这时考

　     虑状态转移方程，当前的数有两种选择,

　     取或不取。

　　   第一种情况

　   　不取，那么第i-1个数有可能取也有可能不取。显然两种情况jC:\Users\ASUS\Desktop的值转移时都不会改变，所以易得转移方程：

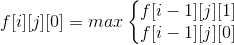
　　   第二种情况

　　　取，那么第i-1个数同样也有两种选择。取的时候，又可以分成两种情况：1.从第i个数开始为新的一组数；2.第i个数与第i-1个数为同一组。　　　　不取，那么第i个数肯一　

　　　组新的数，所以得转移方程：

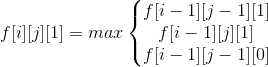
　　代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1000010;//打常数是个好习惯 
int n;
int ans,a[MAXN],f[MAXN][4][2];
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i) scanf("%d",&a[i]);
    memset(f,-127,sizeof(f));
    f[0][0][0]=0;//初始化 
    for(int i=1;i<=n;++i)
        for(int j=0;j<=3;++j){
            f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]);//当前数不取 
            if(j) f[i][j][1]=max(f[i-1][j-1][0]+a[i],f[i-1][j-1][1]+a[i]);
            f[i][j][1]=max(f[i][j][1],f[i-1][j][1]+a[i]);//当前数取 
        }
    printf("%d",max(f[n][3][0],f[n][3][1])); 
    return 0;
}

（某种）数列问题

原文：https://www.cnblogs.com/Ymyself/p/11794488.html