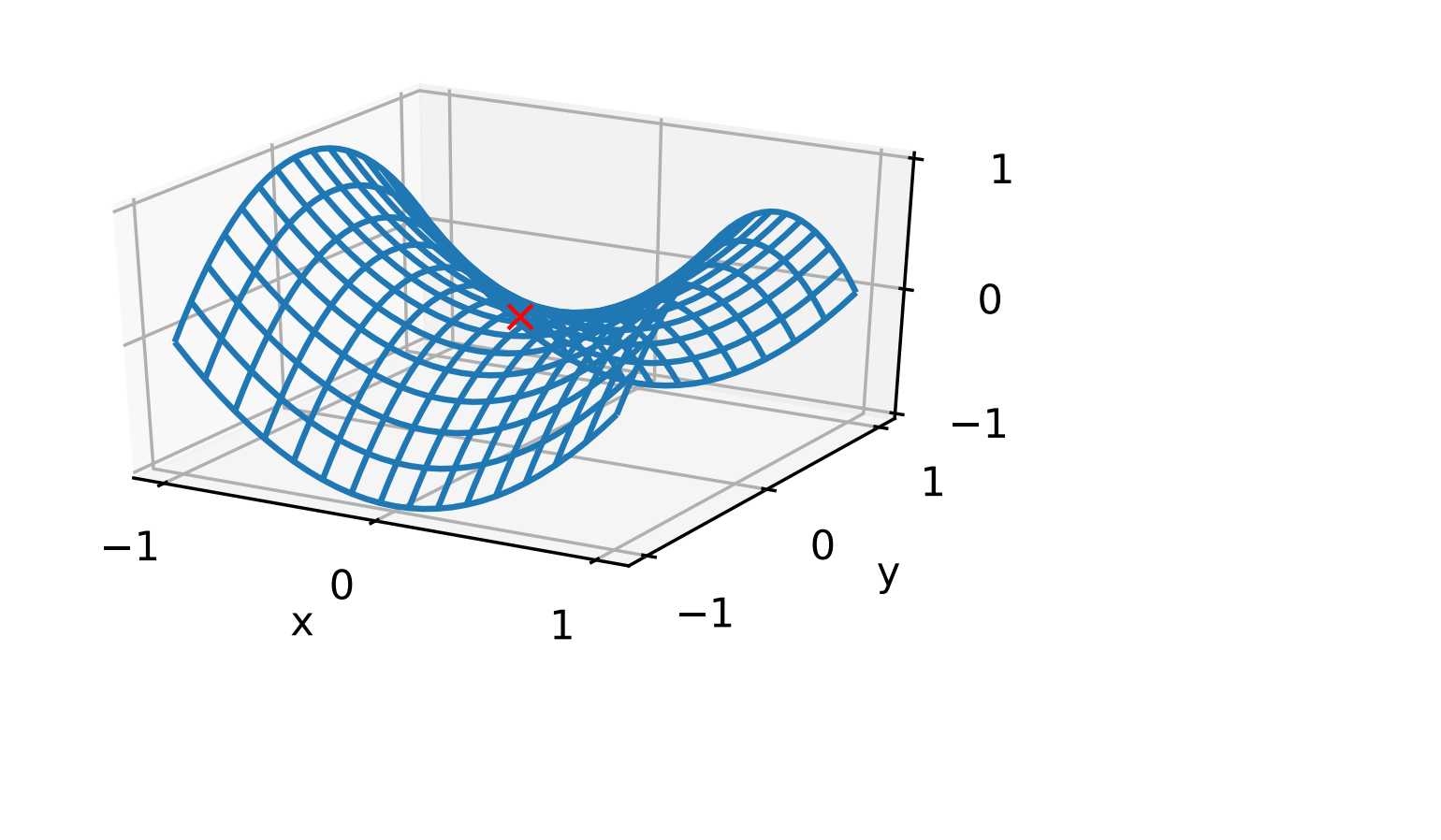
在图的鞍点位置,?标函数在x轴?向上是局部最小值,但在y轴?向上是局部最?值。
假设?个函数的输?为k维向量,输出为标量,那么它的海森矩阵(Hessian matrix)有k个特征值(参?附录中“数学基础”?节)。该函数在梯度为0的位置上可能是局部最小值、局部最?值或者鞍点。
•当函数的海森矩阵在梯度为零的位置上的特征值全为正时,该函数得到局部最小值。
• 当函数的海森矩阵在梯度为零的位置上的特征值全为负时,该函数得到局部最?值。
•当函数的海森矩阵在梯度为零的位置上的特征值有正有负时,该函数得到鞍点。
随机矩阵理论告诉我们,对于?个?的?斯随机矩阵来说,任?特征值是正或者是负的概率都
是0.5 [1]。那么,以上第?种情况的概率为 0.5^k。由于深度学习模型参数通常都是?维的(k很
?),?标函数的鞍点通常?局部最小值更常?。
原文:https://www.cnblogs.com/zjuhaohaoxuexi/p/11805101.html