T1:
? 法一:考虑到找最长border等价与找最短循环节
? 于是对与原串跑一边kmp,求出最短循环节
? 判断\((m-nxt[m])|m ?\) 若成立,则需循环节为\((m-nxt[m])\),否则为m
?
? 法二:考虑到当\(n>=2\)时中间的一定是合法的,所以将原串复制一遍,跑一下kmp即可
?
T2:
? 神(du)仙(liu)题
? 考虑新加的边只能走一次,于是可以先在原图上处理,再对新边进行计算
? 首先预处理两个数组:
? ? f[i],表示从点i出发的胜率(即走奇数条边后无路可走的概率)
? &emps; p[i][0/1],表示从s开始,走偶/奇数条边到达i的概率
? 当连接(i,j)这条边的时候,考虑三种情况:
? ? 1.不经过点i
? ? 2.经过点i,不走(i,j)
? ? 3.经过点i,走(i,j)
? 三种情况胜利的概率分别为:
? ? 1.\(f[s]-(p[i][0]*f[i]+p[i][1]*(1-f[i]))\)
? ? 2.\((p[i][0]*f[i]+p[i][1]*(1-f[i]))*out_i/(out_i+1)\)
? ? 3.\((p[i][1]*f[j]+p[i][0]*(1-f[j]))/(out_i+1)\)
? 化简一下式子之后就简单了
?
T3:
? 这道还是很友好的(大概吧)
? 考虑两种情况:自环/非自环
? 自环很简单,答案就是\(\lceil len_{直径}/2 \rceil\)
? 非自环的话可以分4种情况
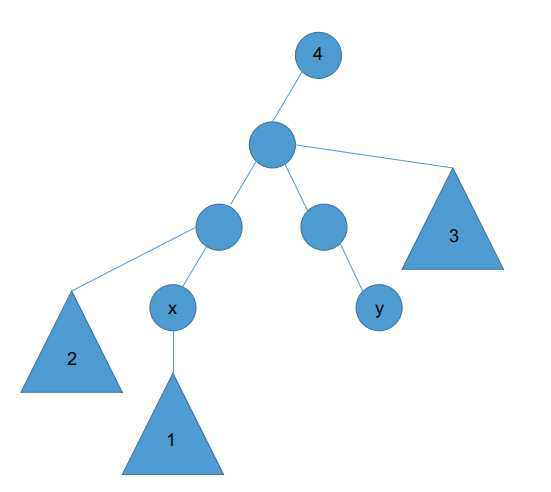
? 1.直接统计子树最长链
? 2.处理数组g[i]表示从\(fa_i\)向下走,不走i这颗子树的最长链,再倍增统计一下
? 3.处理出最长/次长/三长链
? 4.处理数组t[i]表示从i向上走的最长长度
? 然后就没了
原文:https://www.cnblogs.com/Gkeng/p/11809076.html