1, 2, 5, 14 ... 如果打表找到这样一列数,那么答案很有可能就是卡特兰数了
卡特兰数的通项公式F(n) = C(2n, n)/(n+1) = C(2n, n) - C(2n, n+1) ;
卡特兰数是个神奇的数列,有着很多有趣的应用
1到n按顺序入栈,随时可以出栈, 问出栈顺序共有多少种 ?
ans: 卡特兰数....之后的答案都是卡特兰数就不写了
证明: 这类组合数学问题,分类是关键,我们以1出栈时前面一共进去了k(1, 2...n)个数分类,不重复,不遗漏;
以1为分界线,前面k-1个数的排列和后面n-k个数的排列互不影响,根据乘法原理F(n) = F(k-1)*F(n-k) (k=1, 2, 3...n)
而这个递推式就是卡特兰数的递推式了! 为什么?紫书上好像有,先跳过;
这是最经典的一个例子
改编:一道阿里巴巴的笔试题目:说16个人按顺序去买烧饼,其中8个人每人身上只有一张5块钱,另外8个人每人身上只有一张10块钱。烧饼5块一个,开始时烧饼店老板身上没有钱。16个顾客互相不通气,每人只买一个。问这16个人共有多少种排列方法能避免找不开钱的情况出现。
入栈出栈的例子可以等效为0表示出栈1表示入栈一个2n的01序列,问对于每个i(1, n)都满足前面1的个数>=1的排列有多少种
这道题就可以把5块当成1,10块当成0,答案同样为卡特兰数
n*n的方格地图中,从左下角到右上角,不跨越对角线(可以到达但是不能跨越对角线)的路径数, 例如4×4方格地图中
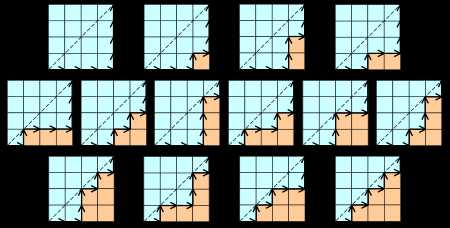
ans: 同样可以把向上当成0向右当成1,问题转化为2n长的01序列,与上面相同;
n对括号正确匹配组成的字符串数
左右括号分别为10, 上同;
n+1个数相乘,所有的括号方案数 (未懂)
例如, 4个数相乘的括号方案为:((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))
n个节点形成不同二叉树个数(乘法原理)
拥有 n+1 个叶子节点的二叉树的数量(未懂)
例如 4个叶子节点的所有二叉树形态:

n+2条边的多边形,能被分割成三角形的方案数(紫书上有证明 乘法原理)
例如 6边型的分割方案有:

圆上2n个点连成n条不相交线段的方法数 (从小到大编号)
原文:https://www.cnblogs.com/ertuan/p/11594925.html