首先先看一下左旋与右旋
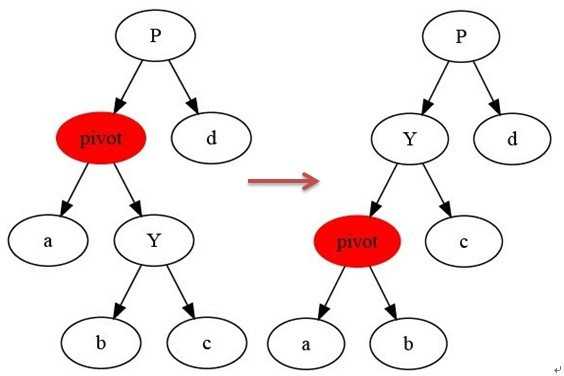
先说左旋
代码可以这样写
1 node *leftRotate(node *root) { 2 node *t = root->right; 3 node *u = t->left; 4 t->left = root; 5 root->rigt = u; 6 return t; 7 }
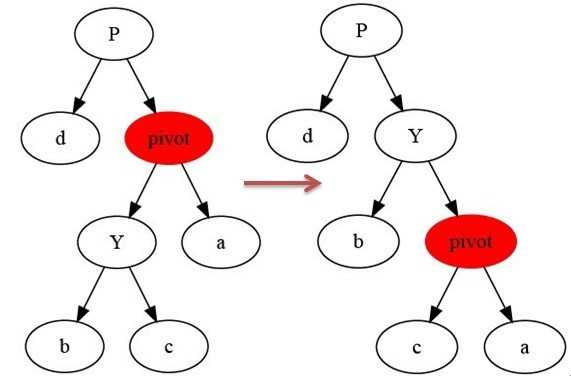
那么右旋相反操作就行了。
1.AVL树的C++实现
1 #include <iostream> 2 #include <queue> 3 4 using namespace std; 5 6 typedef struct node 7 { 8 int data; 9 int height; 10 struct node *left; 11 struct node *right; 12 } node; 13 14 int max(int a, int b) 15 { 16 return a > b ? a : b; 17 } 18 19 // Returns a new Node 20 21 node *createNode(int data) 22 { 23 node *nn = new node(); 24 nn->data = data; 25 nn->height = 0; 26 nn->left = NULL; 27 nn->right = NULL; 28 return nn; 29 } 30 31 // Returns height of tree 32 33 int height(node *root) 34 { 35 if (root == NULL) 36 return 0; 37 return 1 + max(height(root->left), height(root->right)); 38 } 39 40 // Returns difference between height of left and right subtree 41 42 int getBalance(node *root) 43 { 44 return height(root->left) - height(root->right); 45 } 46 47 // Returns Node after Right Rotation 48 49 node *rightRotate(node *root) 50 { 51 node *t = root->left; 52 node *u = t->right; 53 t->right = root; 54 root->left = u; 55 return t; 56 } 57 58 // Returns Node after Left Rotation 59 60 node *leftRotate(node *root) 61 { 62 node *t = root->right; 63 node *u = t->left; 64 t->left = root; 65 root->right = u; 66 return t; 67 } 68 69 // Returns node with minimum value in the tree 70 71 node *minValue(node *root) 72 { 73 if (root->left == NULL) 74 return root; 75 return minValue(root->left); 76 } 77 78 // Balanced Insertion 79 80 node *insert(node *root, int item) 81 { 82 node *nn = createNode(item); 83 if (root == NULL) 84 return nn; 85 if (item < root->data) 86 root->left = insert(root->left, item); 87 else 88 root->right = insert(root->right, item); 89 int b = getBalance(root); 90 if (b > 1) 91 { 92 if (getBalance(root->left) < 0) 93 root->left = leftRotate(root->left); // Left-Right Case 94 return rightRotate(root); // Left-Left Case 95 } 96 else if (b < -1) 97 { 98 if (getBalance(root->right) > 0) 99 root->right = rightRotate(root->right); // Right-Left Case 100 return leftRotate(root); // Right-Right Case 101 } 102 return root; 103 } 104 105 // Balanced Deletion 106 107 node *deleteNode(node *root, int key) 108 { 109 if (root == NULL) 110 return root; 111 if (key < root->data) 112 root->left = deleteNode(root->left, key); 113 else if (key > root->data) 114 root->right = deleteNode(root->right, key); 115 116 else 117 { 118 // Node to be deleted is leaf node or have only one Child 119 if (!root->right) 120 { 121 node *temp = root->left; 122 delete (root); 123 root = NULL; 124 return temp; 125 } 126 else if (!root->left) 127 { 128 node *temp = root->right; 129 delete (root); 130 root = NULL; 131 return temp; 132 } 133 // Node to be deleted have both left and right subtrees 134 node *temp = minValue(root->right); 135 root->data = temp->data; 136 root->right = deleteNode(root->right, temp->data); 137 } 138 // Balancing Tree after deletion 139 return root; 140 } 141 142 // LevelOrder (Breadth First Search) 143 144 void levelOrder(node *root) 145 { 146 queue<node *> q; 147 q.push(root); 148 while (!q.empty()) 149 { 150 root = q.front(); 151 cout << root->data << " "; 152 q.pop(); 153 if (root->left) 154 q.push(root->left); 155 if (root->right) 156 q.push(root->right); 157 } 158 } 159 160 int main() 161 { 162 // Testing AVL Tree 163 node *root = NULL; 164 int i; 165 for (i = 1; i <= 7; i++) 166 root = insert(root, i); 167 cout << "LevelOrder: "; 168 levelOrder(root); 169 root = deleteNode(root, 1); // Deleting key with value 1 170 cout << "\nLevelOrder: "; 171 levelOrder(root); 172 root = deleteNode(root, 4); // Deletin key with value 4 173 cout << "\nLevelOrder: "; 174 levelOrder(root); 175 return 0; 176 }
原文:https://www.cnblogs.com/chenguifeng/p/11815125.html