1 #简单神经病网络 m-p 模型 2 #模型说明,对于输入矩阵 X = [x1 x2 ... xn], 有对应权重矩阵 W=[w1 w2 ... wn] W‘=np.transpose(W) 3 #对于 f = f(X·W‘) ,给定阈值θ 4 # 当 X·W‘ > θ , f = 1, 5 # 当 X·W‘ < θ , f = 0, 6 import numpy as np 7 x = 10 * np.random.rand(5) #先随机生成 5 个 0--1 的种子,之后 *10,即种子大小为 0--10 8 print(‘x = ‘,x) 9 10 w = np.transpose(np.random.rand(5)) # w 为权重矩阵,先生成 1*5 矩阵,之后转置 11 print(‘w = ‘,w) 12 13 θ= 5 14 15 f1 = x.dot(w) - θ 16 17 print(‘x.dot(w) - θ = ‘,f1) 18 19 if f1 > 0: 20 f = 1 21 else: 22 f = 0 23 24 print(‘f = ‘,f)
与M-P模型相似,但是感知机模型初衷是为了完成数据分类的问题
感知机的数学表达式如下: f(x) = sign( w·x + b) 其中sign(x)为符号函数
化简后可以表示为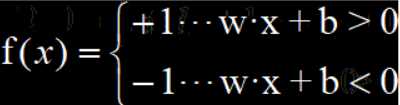
从几何意义上来看,二分类感知机能够将两类数据进行分类。
感知机的优点是很容易处理线性可分问题,缺点是不能处理异或问题,即非线性问题。因而出现了多层感知机来处理非线性问题。
多层感知机与感知机的区别在于,输入层和输出层之间加入了 n 个隐藏层 ( n >= 1),同时多层感知机具备了一种后向传播能力。
对于同一幅图片,比如下图:

目标识别:对于我们输入的图像,计算机能够识别出我们此处的皮卡丘并给他打上矩形框并且标上标签名
语义分割:而语义分割则更多的在于分割图像,它将图片中皮卡丘的轮廓描绘出并且与图片中的其他分隔开
监督学习:举个例子,现在有一堆苹果和一堆梨,需要计算机识别。监督学习就是开始的时候计算机不知道什么是苹果什么是梨,于是我们拿一堆苹果和一堆梨去让计算机学习,多轮训练之后计算机已经能够分辨二者后,机器会形成自己的判断并且能够给以苹果和梨不同的特征描绘。
无监督学习:还是上面的例子,初始时计算机也并不知道什么是苹果什么是梨,但是我们也不给他训练让他自己判断,计算机根据二者的不同点自己分类总结,并且优化每一次判断的参数,最后能够自己将苹果和梨分开。这更贴近我们理解的“人工智能”。
两者利弊:
监督学习需要我们花费大量时间和输入原始数据,但是得到的模型结果更符合我们训练模型的初衷。
无监督学习能够自己寻找数据之间隐藏的特征和关系,更加具有创造性,有时能挖掘到意想不到的特性,但是最终的结果有不可控性,可能往坏的方向发展。
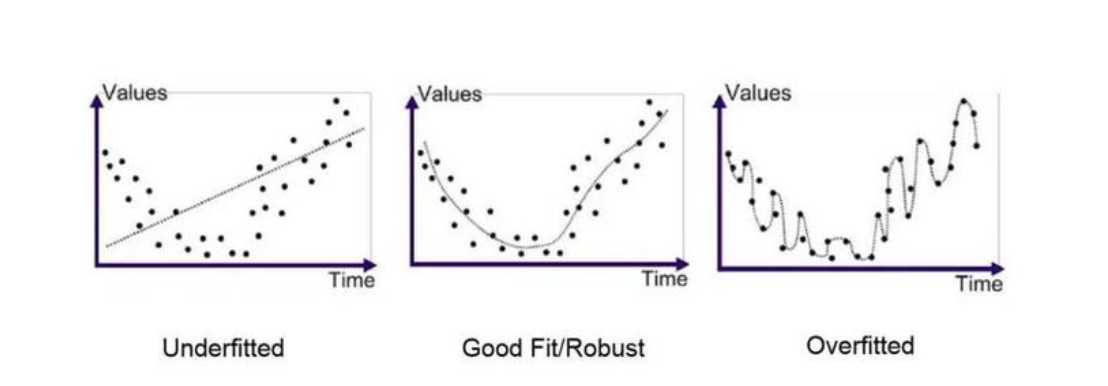
优点:对噪声不敏感
缺点:对已有数据的匹配性很差
改进措施:
优点:对已有数据匹配度很高
缺点:对噪声极度敏感
改进措施:
后向传播实质上就是函数映射结果对每个参数求偏导,最后将偏导结果作为微调值。通过不断的微调使得模型的参数最优化。
例如 f = (x+y) * z 其中 x = 2 、y = 5 、z = 3 那么 f 对 x , y , z 的偏导分别为 3、3、7.
举一个更复杂网络的后向传播例子:
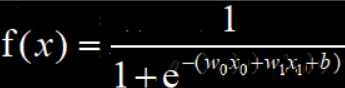
其中 x0 = 1、x1=1、b=-1、w0=0.5、w1=-0.5
则 x0 = 1的后向传播微调值为 f(x) 对 x0 的偏导0.125,x1 = 1的后向传播微调值为 f(x) 对 x1的偏导 0.125
损失用来度量模型的预测值和真实值之间的差距。损失越大,说明预测值和实际值偏差大,模型预测不准确,反之亦然。
对模型优化的最终目的是尽可能地在不过拟合的情况下降低损失值。
常用损失函数如下:
1.均方差误差 Mean Square Error (MSE)
2.均方根误差 Root Mean Square Error (RMSE)
3.平均绝对误差 Mean Absolute Error (MAE)
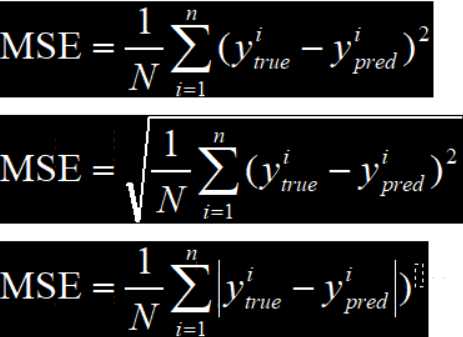
常用优化函数如下:
全局梯度下降,训练样本总数为 n , j=0,1,...,n θ是学习速度,J(θ)是损失函数
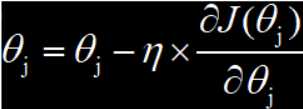
学习速率用于控制梯度更新的快慢。如果学习速率过快,参数的更新跨度就会变大,极容易出现局部最优和抖动;如果学习速率过慢,梯度更新的迭代次数就会增加,参数优化所需要的时间也会变长。
全局梯度下降有一个很大的问题:模型的训练依赖于整个训练集,所以增加了计算损失值的时间成本和模型训练过程中的复杂度,而参与训练的数据量越大,这个问题就越明显。
批量梯度下降就是将整个参与训练的数据集划分为若干个大小差不多的训练数据集,然后每次用一个批量的数据来对模型进行训练,并以这个批量计算得到的损失值为基准,来对模型中的全部参数进行梯度更新,默认这个批量只使用一次,直到所有批量全都使用完毕。
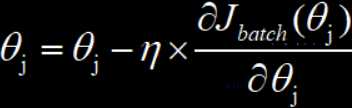
批量梯度下降的优点是计算损失函数的时间成本和模型训练的复杂度将会大大降低;但是缺点在于很容易导致优化函数的最终结果是局部最优解。
随机梯度下降是通过随机的方式,从整个参与训练的数据集中,选择一部分来参与模型的训练,所以只要我们随机选取的数据集大小合适,就不用担心计算损失函数的时间成本和模型训练的复杂度,而且与整个参预训练的数据集的大小没有关系。
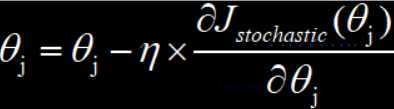
随机梯度下降很好的提升了训练速度,但是会在模型的参数优化过程中出现抖动的情况,原因在于我们选取参预训练的数据集是随机的,所以模型收到随即训练数据集中噪声数据的影响,又因为有随机的因素,所以也容易导致模型最终得到局部最优解。
Adam自适应时刻估计法是一种比较智能的优化函数方法,它通过让每个参数获得自适应的学习率,来达到优化质量和速度的双重提升。
For instance,一开始进行模型参数训练的时候,损失值比较大,则此时需要使用较大的学习速率让模型参数进行较大的梯度更新,但是到了后期我们的损失值已经趋向于最小了,这时就需要使用较小的学习速率吧来让模型参数进行较小的参数更新。。
Adam学习速率好、收敛速率快,是一种比较好的优化函数。
激活函数类似一个递归定义,假如激活函数是取输入值和 0 比较的最大值,那么,对于单层神经网络, f(x) = max(W·X + b , 0),那么同样的,对于双层神经网络,f(x) = max(W2·max(W1·X + b1 , 0)+b2,0)
因此我们可以看出,如果不引入激活函数,那么不管我们有多少层神经网络,最后的输出都一样会是一个线性函数,而引入激活函数使得我们的模型有了非线性因素。
常用的非线性激活函数如下:
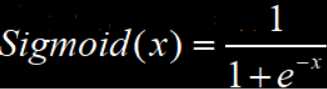
Sigmoid函数的激活输出过程与生物神经网络工作机理十分相似,但是Sigmoid作为激活函数的缺点在于会导致模型的梯度消失,因为SigMoid的导数取值区间为[0,0.25]。根据链式法则,如果每层神经网络的输出节点都用Sigmoid作为激活函数,则每一层都要乘一次Sigmoid的导数值,即便每次都乘以最大的0.25,模型到了一定深度,梯度还是会消失。
其次Sigmoid函数值恒大于0,使得模型在优化的过程中收敛速度变慢。因为深度神经网络模型的训练和参数优化往往需要消耗大量的时间,所以会导致时间成本过高。因此计算数据时,尽量使用零中新数据,也要尽量保证计算得到的输出结果是零中心数据。
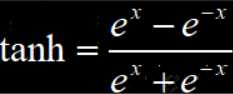
tanh的输出结果是零中心数据,所以解决了模型优化过程中收敛速度变慢的问题。但是tanh的导数取值范围是0~1,仍然不够大,因此后向传播的过程中,仍然会出现梯度消失的情况。
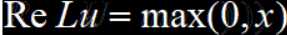
ReLU,修正线性单元,是目前在深度神经网络模型中使用率最高的激活函数,他的收敛速度非常快,其计算效率远远高于Sigmoid和tanh,但是ReLU也存在着输出不是零中心数据的问题,这可能导致某些神经元永远得不到激活,并且这些神经元的参数永远得不到更新。这一般是由于模型参数在初始化时使用了全正或全负的值,或者在后向传播过程中设置的学习速率太快而导致.解决办法可以是对模型使用更高级的初始化方法比如Xavier,以及设置合理的后向传播学习速率,推荐使用自适应的算法如Adam。
ReLU也在被不断地改进,现在已经有很多ReLU的改进版本,例如Leaky-ReLU、R-ReLU等。
CPU(Central Processing Unit,中央处理器)与GPU(Graphics Processing Unit图像处理器)用处不同。CPU是一台计算机的处理核心,主要负责计算机的控制命令处理和核心运算输出,GPU是一台主机的现实处理核心,主要负责对计算机中的图形和图像的处理与运算。差异主要如下:
每天进步一小点,加油!共勉
原文:https://www.cnblogs.com/Rebel3/p/11821541.html