
题目分析
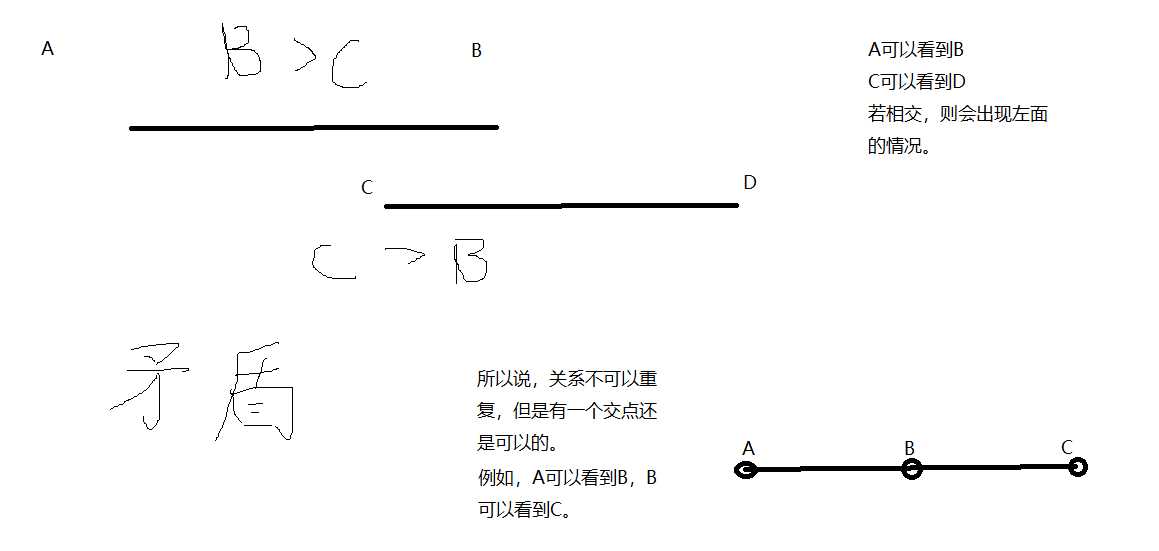
本题采用差分数组,便于将一个区间的数全部减一,初始化height[1]=h(表示当前所有的牛身高都是h,因为height数组在全局变量中,所以全部为0,根据差分数组的性质:差分数组的前缀和(b[1]+b[2]+...+b[i])等于数组中的某个元素(a[i]))。有上述分析可知,区间不会有交集,所以将所给的区间端点内部的所有数-1(因为求最大身高所以-1即可),最后求每一项的前缀和,得到所有牛可能的最大身高。
#include <iostream>
#include <set>
using namespace std;
const int N = 10010;
int height[N];
int main()
{
int n, p, h, m;
cin >> n >> p >> h >> m;
height[1] = h;
set<pair<int, int> > existed; // 题目中给定的数据可能会有重复,故用set去重
for(int i = 1, a, b; i <= m; ++ i)
{
cin >> a >> b;
if(a > b) swap(a, b); // 端点的大小要进行比较
if(!existed.count({a, b}))
{
existed.insert({a, b});
height[a + 1] --; // 差分数组的应用,区间[a + 1, b - 1]内所有的数-1
height[b] ++;
}
}
for(int i = 1; i <= n; ++ i)
{
height[i] += height[i - 1];
cout << height[i] << endl; // 前缀和得到每头牛的身高
}
return 0;
}
原文:https://www.cnblogs.com/mjn1/p/11823105.html