机器学习——一元线性回归（二）

一、回归背景(Regression Background)

回归最早由Francis Galton提出，他还是著名生物学家，进化论奠基人Charles Darwin的表弟。Galton受进化论的影响，把该思想进行人类研究，从一串角度解释个体差异形成的原因。

Francis Galton研究人类身高，进行归纳普遍规律，这是最早的回归。

二、一元线性回归(Unary linear Regression)

• 回归分析(Regression analysis)用来建立方程模拟两个或者多个变量之间如何关联
• 被预测的变量叫做：因变量(dependent variable), 输出(output)
• 被预测的变量叫做：自变量(independent variable), 输入(input)
• 一元线性回归包含一个自变量和一个因变量
• 以上两个变量关系进行一条直线模拟
• 如果包含两个以上的因变量，则称作多元回归分析(multiple regression)

h(θ)=θ0+θ1X

这个方程对应的图形是一条直线，称作回归线，其中θ1为回归线的斜率，θ0为回归线的截距

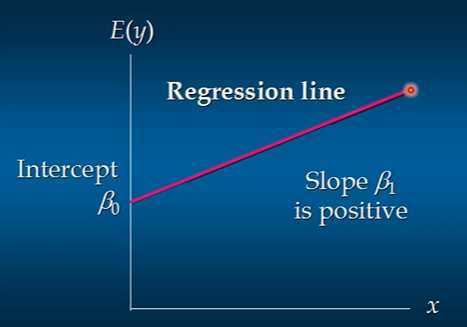
正相关

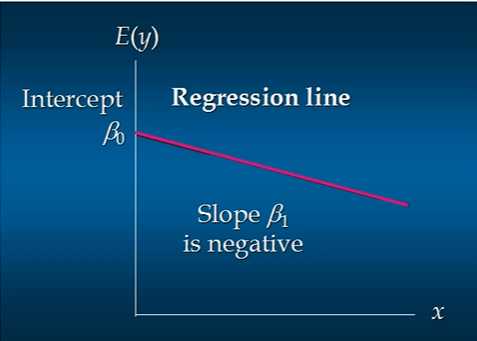
负相关

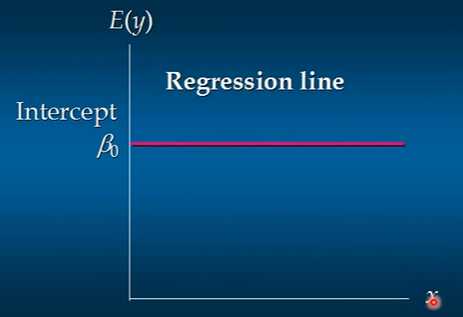
无关

三、代价函数(相关系数/决定系数)

1.代价函数(Cost Function)

• 最小二乘法
• 真实值y，预测值hθ(x)，则误差平方为(y-hθ(x))^2,
• 找到合适的参数，使得误差平方和最小

$$
\zeta(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(y^i-h_\theta(x^i))^2
$$

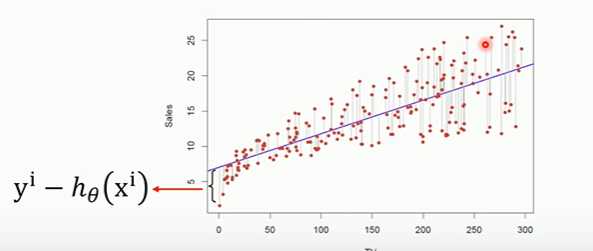
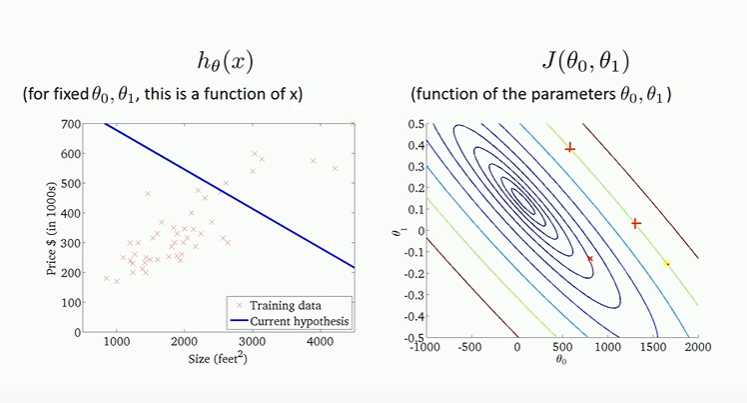
Hypothesis:
$$
h_\theta(x)=\theta_0+\theta_1
$$
Simplified:
$$
h_\theta(x)=\theta_1x
$$

Parameters:
$$
\theta_0,\theta1
$$
Simplified:
$$
\theta_1
$$

Cost Function:
$$
J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2
$$
Goal:
$$
\min_{\theta_0,\theta_1}J(\theta_0,\theta_1)
$$
Simplified:
$$
\min_{\theta_1}J(\theta_1)
$$

2.相关系数

我们使用相关系数来衡量线性相关的强弱

3.决定系数

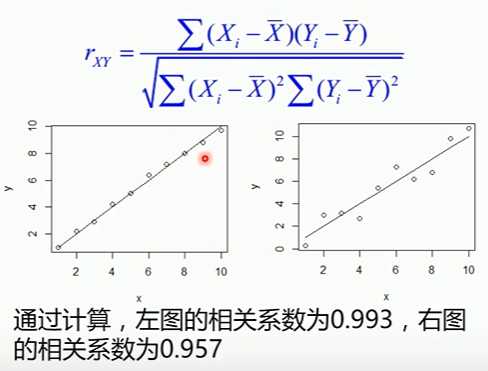
相关系数R^2（coefficient of determination）是用来描述两个变量之间的线性关系的，但决定系数适用范围更广，可以用于描述非线性或者有2个及两个以上自变量的相关关系。可以来评价模型效果。

总平方和（SST）：
$$
\sum_1^n(y_i-\overline{y})^2
$$
回归平方和（SSR）：
$$
\sum_i^n(\hat{y}-\overline{y})^2
$$
残差平方和（SSE）：
$$
\sum_{i=1}^n(y_i-\hat{y})^2
$$

他们的三者关系是：
$$
SST=SSR+SSE
$$

决定系数：
$$
R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}
$$

四、梯度下降法

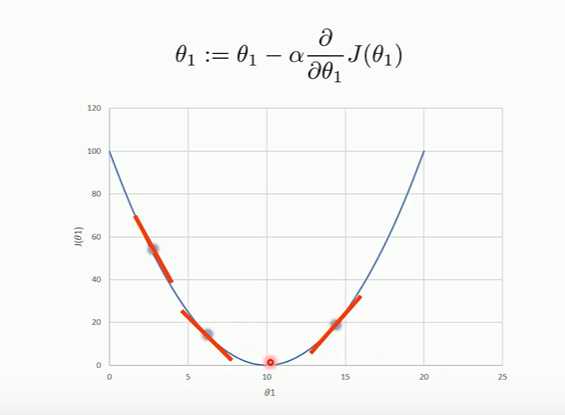
梯度下降法是一个优化算法，来优化代价函数，使代价函数变小
$$
Have?some?function?J(\theta_0,\theta_1)
$$

$$
Want?\min_{\theta_0,\theta_1}(\theta_0,\theta_1)
$$

• 初始化θ0,θ1
• 不断改变θ0,θ1，直到J(θ0,θ1)到达一个全局最小值，局部最大值

机器学习——一元线性回归（二）

原文：https://www.cnblogs.com/littlepage/p/11839438.html