先来了解一下浮点数在计算机中是以什么形式存储的
首先要知道计算机能懂得只有0和1,每一个0和1都占一个位 bit (比特)(Binary Digits):存放一位二进制数,最小的存储单位。
而对于存放一个有小数点的数是如何存储的呢?
对于整数部分,会转换成二进制,使用除2倒取余的方法。
22 / 2 = 11 余0
11 / 2 = 5 余1
5 / 2 = 2 余1
2 / 2 = 1 余0
1 / 2 = 0 余1
22 的二进制转换就是 10110
而对于小数部分,就会乘2取整数的方法。
0.45 * 2 = 0.9 0
0.9 * 2 = 1.8 1
0.8 * 2 = 1.6 1
0.6 * 2 = 1.2 1
0.2 * 2 = 0.4 0
0.4 * 2 = 0.8 0
0.8 * 2 = 1.6 1
0.6 * 2 = 1.2 1
0.2 * 2 = 0.4 0
……
可以发现0.45转化成二进制的时候是无限循环的
二进制转换完成,22.45 --> 10110.011100110......
得到这个二进制浮点数之后,计算机是怎么把他表示为没有小数点的字符呢?
这就用到了小学使用的科学计数法:
10110.011100110 可以写为 1.0110011100110

过程中我们发现,小数的转换有可能会产生无限循环的情况,想要做的最精确的记录22.45,计算机需要无限大的空间来记录01
那么 IEEE标准 就规定:
32位单精度(java中的float),使用32位(bit)来存储
64位双精度(double), 使用64位储存
在Java中,对于浮点类型的数据采用单精度类型(float)和双精度类型(double)来存储,float数据占用4个字节32bit,double数据占用8个字节64bit。
那么它们是如何来分配内存的呢?其实不论是float还是double在存储方式上都是遵从IEEE的规范的,float遵从的是IEEE R32.24 ,而double 遵从的是R64.53。
无论是单精度还是双进度在存储中分为三个部分:
1.符号位(Sign):0代表正,1代表负
2.指数位(Exponent):用于存储科学计数法中的指数数据,并且采用移位存储
3.尾数部分(Mantissa):尾数部分
其中 float 的存储方式如下图所示:
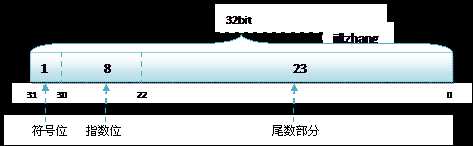
而 double 的存储方式如下:
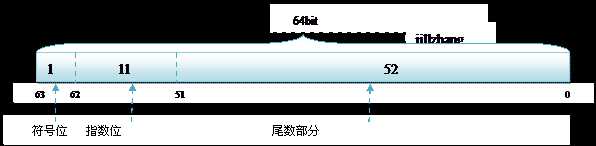
原文:https://www.cnblogs.com/niujifei/p/11841221.html