Input输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c...y,z组成的字符串S
两组case之间由空行隔开(该空行不用处理)
字符串长度len <= 110000Output每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度.
Sample Input
aaaa abab
Sample Output
4 3
废话不多说,上代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 const int maxn=110010; 8 char str[maxn];//原字符串 9 char tmp[maxn<<1];//转换后的字符串 10 int Len[maxn<<1]; 11 //转换原始串 12 int INIT(char *st) 13 { 14 int i,len=strlen(st); 15 tmp[0]=‘@‘;//字符串开头增加一个特殊字符,防止越界 16 for(i=1;i<=2*len;i+=2) 17 { 18 tmp[i]=‘#‘; 19 tmp[i+1]=st[i/2]; 20 } 21 tmp[2*len+1]=‘#‘; 22 tmp[2*len+2]=‘$‘;//字符串结尾加一个字符,防止越界 23 tmp[2*len+3]=0; 24 return 2*len+1;//返回转换字符串的长度 25 } 26 //Manacher算法计算过程 27 int MANACHER(char *st,int len) 28 { 29 int mx=0,ans=0,po=0;//mx即为当前计算回文串最右边字符的最大值 30 for(int i=1;i<=len;i++) 31 { 32 if(mx>i) 33 Len[i]=min(mx-i,Len[2*po-i]);//在Len[j]和mx-i中取个小 34 else 35 Len[i]=1;//如果i>=mx,要从头开始匹配 36 while(st[i-Len[i]]==st[i+Len[i]]) 37 Len[i]++; 38 if(Len[i]+i>mx)//若新计算的回文串右端点位置大于mx,要更新po和mx的值 39 { 40 mx=Len[i]+i; 41 po=i; 42 } 43 ans=max(ans,Len[i]); 44 } 45 return ans-1;//返回Len[i]中的最大值-1即为原串的最长回文子串额长度 46 } 47 int main() 48 { 49 while(~scanf("%s",str)) 50 { 51 int len=INIT(str); 52 int ans=MANACHER(tmp,len); 53 printf("%d\n",ans); 54 } 55 return 0; 56 }
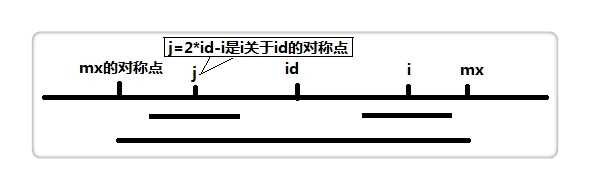
设置两个变量,mx 和 id 。mx 代表以 id 为中心的最长回文的右边界,也就是mx = id + p[id]。
假设我们现在求p[i],也就是以 i 为中心的最长回文半径,如果i < mx,如上图,那么:
if (i < mx) p[i] = min(p[2 * id - i], mx - i);2 * id - i为 i 关于 id 的对称点,即上图的 j 点,而p[j]表示以 j 为中心的最长回文半径,因此我们可以利用p[j]来加快查找。
原文:https://www.cnblogs.com/RE-TLE/p/11842958.html