从$geography.in$读入数据。
第一行两个数$n,m$,表示有$n$个点,$m$个时刻。接下来$m$行每行三个数,要么是$1\ u\ v$,要么是$2\ u\ v$,分别表示添加一条无向边和删除一条无向边。
输出答案到$geography.out$。
共$m$行,每行一个数表示连通块大小乘积$\mod 1,000,000,007$。
样例
样例输入:
5 6
1 1 3
1 2 3
1 1 2
1 4 5
1 3 4
2 3 4
样例输出:
2
3
3
6
5
6
样例解释:
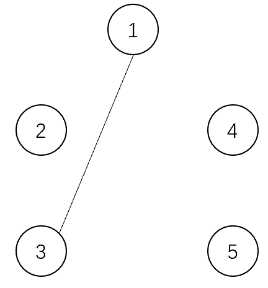
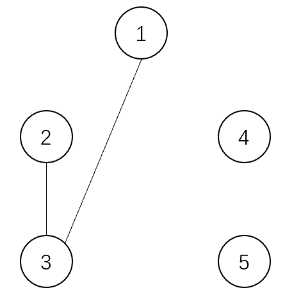
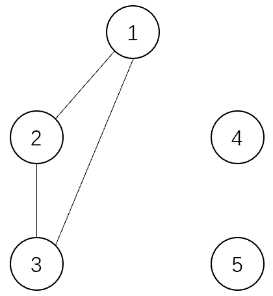
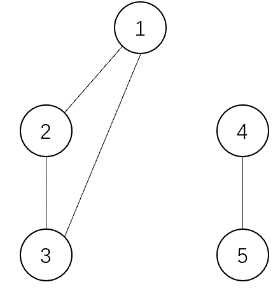
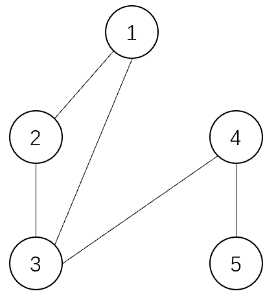
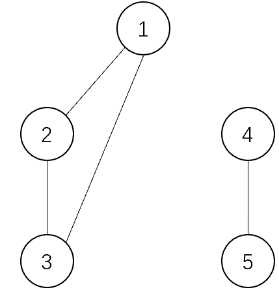
上面是每个时刻操作后的图。乘积分别为:
$$2\times 1\times 1\times 1=2,3\times 1\times 1=3,3\times 1\times 1=3,3\times 2=6,5,3\times 2=6$$
数据范围:
$subtask1:30pts,n\leqslant 1,000,m\leqslant 2,000$。
$subtask2:20pts$,满足没有删除操作。
$subtask3:50pts,n,m\leqslant 100,000$。保证没有重边自环,不会删除不存在的边。
这好像是一道模板题。
具体思路就是将问题离线,然后按时间建一棵线段树,在线段树上分治,递归的时候不断的将边加入并查集,到底层的时候统计答案即可。
需要注意的是还要支持回退,在递归下去的时候记录一下当前修改了哪些点的$father$或者权值,返回的时候直接改回来即可。
时间复杂度:$\Theta(\omega\times n\log n)$。
期望得分:$100$分。
实际得分:$100$分。
#include<bits/stdc++.h>
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
const int mod=1000000007;
struct rec{int nxt,to;}e[200001];
int head[100001],cnt;
map<pair<int,int>,int>mp;
int n,m;
int f[100001],sz[100001],question[100001];
pair<int,int>wzc[100001];
vector<int>tr[400001];
vector<pair<pair<int,int>,pair<int,int>>>vec[400001];
long long qpow(long long x,long long y)
{
long long res=1;
while(y)
{
if(y&1)res=res*x%mod;
x=x*x%mod;y>>=1;
}
return res;
}
int find(int x){return x==f[x]?x:find(f[x]);}
void change(int x,int l,int r,int L,int R,int w)
{
if(r<L||R<l)return;
if(L<=l&&r<=R){tr[x].push_back(w);return;}
int mid=(l+r)>>1;
change(L(x),l,mid,L,R,w);
change(R(x),mid+1,r,L,R,w);
}
void ask(int x,int l,int r,int k)
{
for(int i=0;i<tr[x].size();i++)
{
int fx=find(wzc[tr[x][i]].first);
int fy=find(wzc[tr[x][i]].second);
if(fx==fy)continue;
if(sz[fx]<sz[fy])fx^=fy^=fx^=fy;
vec[x].push_back(make_pair(make_pair(fx,sz[fx]),make_pair(fy,f[fy])));
k=1LL*k*qpow(sz[fx],mod-2)%mod*qpow(sz[fy],mod-2)%mod;
f[fy]=fx;
sz[fx]+=sz[fy];
k=1LL*k*sz[fx]%mod;
}
if(l==r)printf("%d\n",k);
else
{
int mid=(l+r)>>1;
ask(L(x),l,mid,k);
ask(R(x),mid+1,r,k);
}
for(int i=vec[x].size()-1;~i;i--)
{
f[vec[x][i].second.first]=vec[x][i].second.second;
sz[vec[x][i].first.first]=vec[x][i].first.second;
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){f[i]=i;sz[i]=1;}
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d%d",&x,&x,&y);
if(x>y)x^=y^=x^=y;
int now=mp[make_pair(x,y)];
if(!now){mp[make_pair(x,y)]=++cnt;question[cnt]=i;wzc[cnt]=make_pair(x,y);}
else
{
if(question[now]){change(1,1,m,question[now],i-1,now);question[now]=0;}
else question[now]=i;
}
}
for(int i=1;i<=cnt;i++)if(question[i])change(1,1,m,question[i],m,i);
ask(1,1,m,1);
return 0;
}
rp++
原文:https://www.cnblogs.com/wzc521/p/11845067.html