期望，方差，协方差，相关系数，协方差矩阵，相关系数矩阵

1. 期望

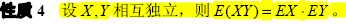
2. 方差

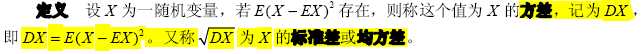
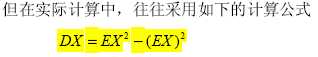
3. 协方差和相关系数

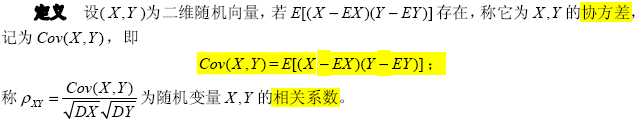
这个定义中“二维”指的是这个随机变量有两个分量：X和Y。把X和Y看做是标量就好。

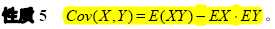
4. 协方差矩阵

 假设X是n个标量随机变量组成的列向量：X=(x₁, x₂, ..., xⁿ)^T。协方差矩阵的定义为Cov=E[(X-E(X))(X-E(X))^T]，即协方差矩阵的每个元素是向量各个元素之间的协方差。假设u_i是X的第i个元素的期望值，即u_i=E(x_i)，则协方差矩阵第(i, j)项为：

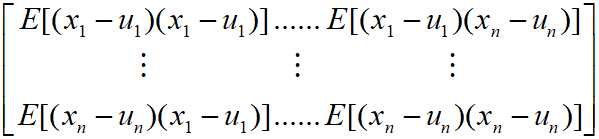
 在机器学习中，理解协方差矩阵的关键在于牢记它计算的是同一个样本不同特征维度之间的协方差，而不是不同样本之间。拿到样本矩阵之后，我们首先要明确一行是样本还是特征维度。一般来说，样本矩阵中一行是一个样本，一列为一个特征维度。所以要按列计算均值（期望），再按行计算出协方差矩阵，把每一行的协方差矩阵相加再除以行数（即样本数），得到样本矩阵的协方差矩阵，公式为：Cov = (∑XX^T)/N，式中N为样本数，X是中心化之后的一个一个样本。下图可帮助理解：

5.相关系数矩阵

 如果样本矩阵的一列表示一个特征维度，则相关系数矩阵的第i行第j列的元素是样本矩阵第i列和第j列的相关系数。下面用python-numpy实现一个简单的求相关系数矩阵的例子：

import numpy as np
featuremat = np.random.rand(8, 2)  # 8个样本，两个特征

# compute mean
mean0 = np.mean(featuremat[:, 0])  # 求第一个特征列的均值
mean1 = np.mean(featuremat[:, 1])  # 求第二个特征列的均值

# comupte standard deviation
std0 = np.std(featuremat[:, 0])
std1 = np.std(featuremat[:, 1])

corref = np.mean((featuremat[:, 0]-mean0)*(featuremat[:, 1]-mean1)) / (std0*std1)
print(‘corref: ‘, corref)
print(‘corref matrix: ‘)
print(np.corrcoef(featuremat.T))    # 求特征列之间的计算相关系数矩阵

结果如下：

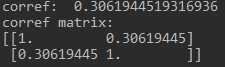
【参考文献】

1. 概率论与数理统计，黄清龙等，北京大学出版社

期望，方差，协方差，相关系数，协方差矩阵，相关系数矩阵

原文：https://www.cnblogs.com/picassooo/p/11844825.html