数据结构 -- wk1 基本概念（2）

第一讲 基本概念 - 2 2019-11-15

? 算法（Algorithm）

? 一个有限指令集

? 接受一些输入（有些情况下不需要输入）

? 产生输出

? 一定在有限步骤之后终止 [不可像操作系统那样，一直运行]

? 每一条指令必须

? 有充分明确的目标，不可以有歧义

? 计算机能处理的范围之内

? 描述应不依赖于任何一种计算机语言以及具体的实现

例一：选择排序的伪码描述

 * List 是数组 还是 链表？

* Swap 是函数 还是 宏？-- 这些都由具体的算法决定

Part 1 - 算法的 空间复杂度 S(n) 和 时间复杂度 T(n) 

1) 空间复杂度 S(n)

根据算法写成的程序在执行时占用存储单元的长度。

这个长度往往与输入数据的规模有关。[N]

空间复杂度过高的算法可能导致使用的内存超限，造成程序非正常中断。

2) 时间复杂度 T(n)

根据算法写成的程序在执行时耗费时间的长度。

这个长度往往也与输入数据的规模有关。

时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。

*对之前的递归算法 [见 基本概念-1 例一]　　N=100000;

1 // recursion
2 void printN(int N){
3     if(N){
4         printN(N-1);
5         printf("%d\n", N);
6     }
7 }

空间占用：首先会将100000存入内存，然后调用printN(99999)；将99999存入内存，再调用printN(99998) ...

空间复杂度：S(N); N为输入数据规模，C为常数[取决于计算机本身]

* 随着N的增加，递归对内存的占用是很严重的

*对之前的计算多项式算法 [见 基本概念-1 例三] ，其时间复杂度T(n)如下：

**计算机计算乘除法的计算量远大于加减法，因此可以通过乘除法，来估算复杂度

 *因此 方法2 比方法1要快很多

在分析算法效率时，通常关注两种复杂度：

最坏情况复杂度 T_worst(n) [通常比较容易计算]

平均复杂度 T_avg(n) [通常难以计算]

T_avg(n) <= T_worst(n) 

Part - 2 复杂度的渐进表示法

T(n) = O(f(n)) 　　// O(n) 为上边界

T(n) = Ω(g(n))　　//  Ω(n) 为下边界

T(n) = Θ(h(n)) = O(f(n)) = Ω(g(n))　　// Θ(n) 上下边界相同

*计算算法复杂度的小技巧 【仅讨论 最大复杂度 O(n)】

1. 两段算法复杂度分别为 T1(n) = O(f1(n))，T2(n) = O(f2(n))

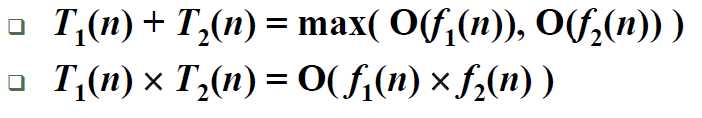
2. T(n) 是关于n的k阶多项式，T(n) = Θ(n^k)

3. for 循环的复杂度 = 循环次数 * 循环体复杂度

4. if-else 结构的复杂度：取决于各分支的复杂度，取分支中最大复杂度，为总体复杂度。

Part - 3 复杂度表格

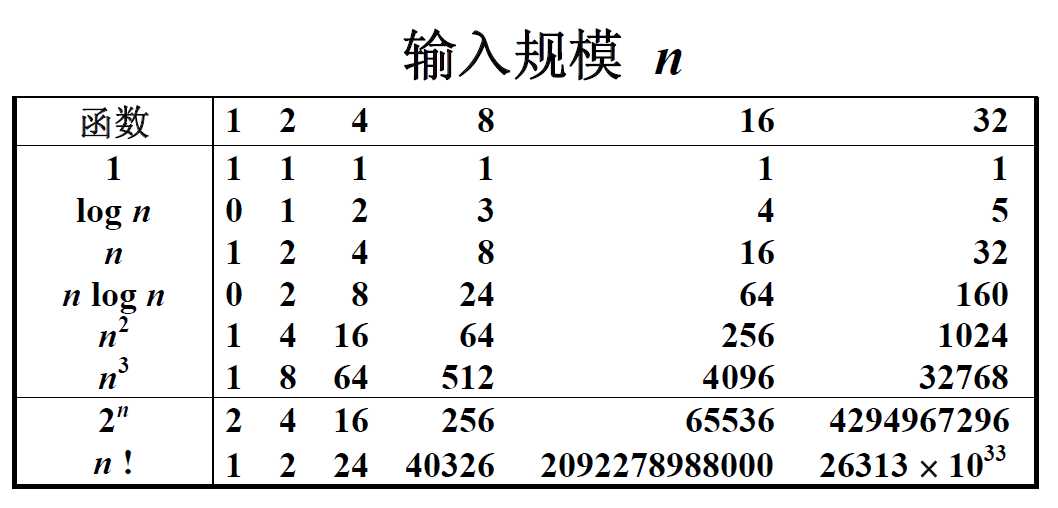
 　　　　　　　　　　　　Table 1，复杂度 1 - n！

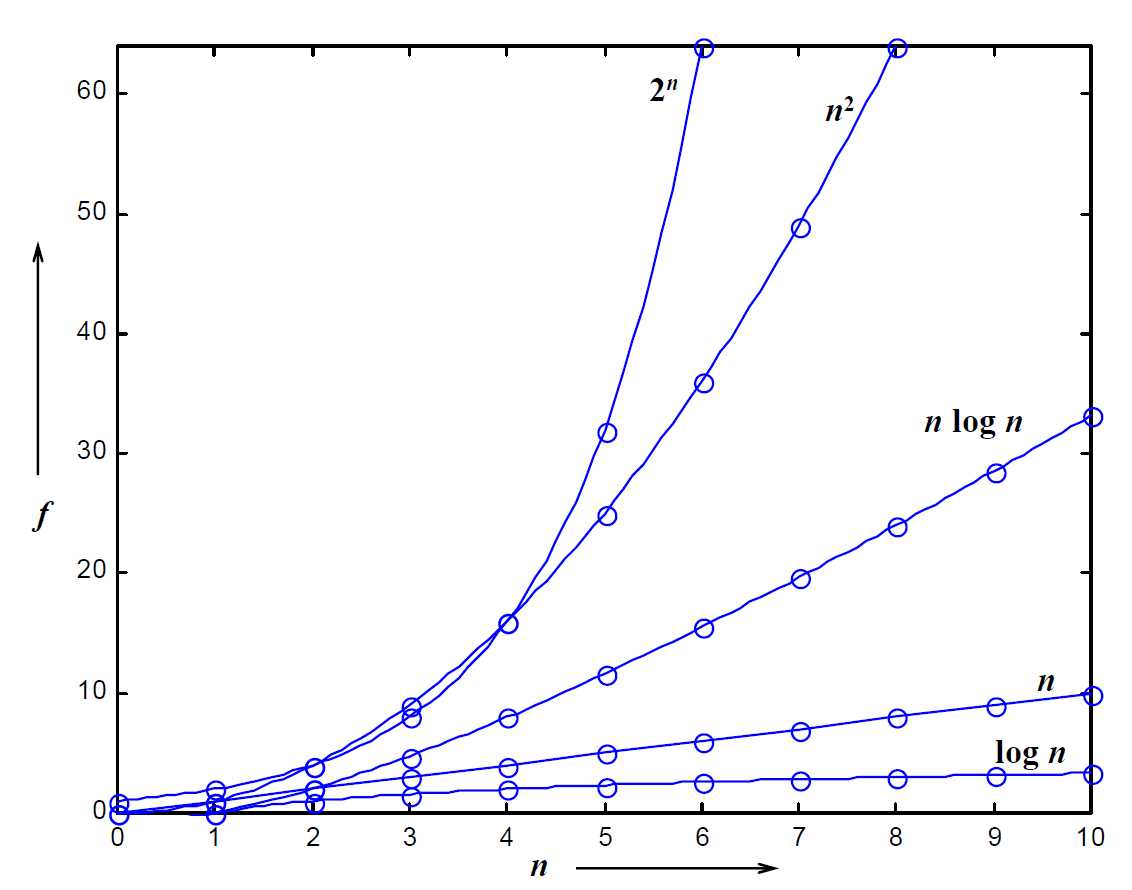
　　　　　　　　　　　　Figure 1，复杂度log n - 2^n

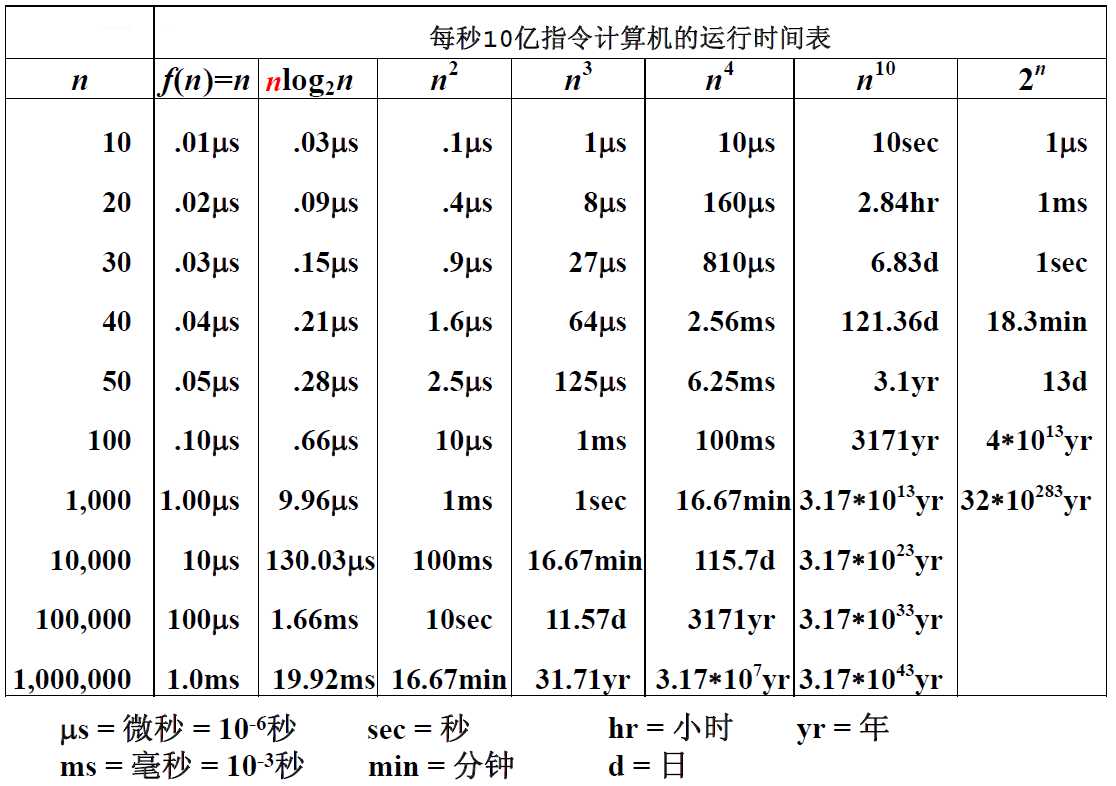
 　　　　　　　　　　Table 2，不同复杂度运行时间 n - 2^n

数据结构 -- wk1 基本概念（2）

原文：https://www.cnblogs.com/SAzSkjEydrD2B9yu/p/11869861.html