最小生成树Prim
最小生成树的定义
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边(度娘原话)
简单来说,就是一个连接所有点且路径和最小的图
Prim的思路
设图的顶点集合为U,树的顶点集合为V
从图中任意一点出发,找到N-1条边(x,y),x∈U,y∈V,且权值最小。
通俗的讲,就是不断找权值最小且不产生闭环的N-1条边
栗子
废话不多说,先上图
如下图所示
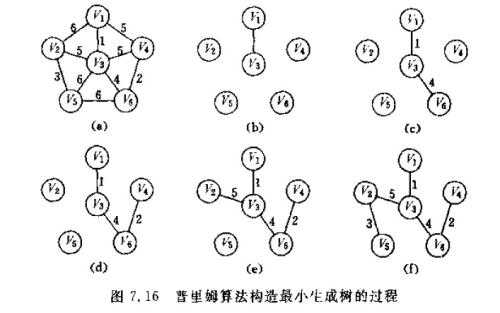
(1)从V3出发
(2)找到边(V3,V1),符合条件且最小,将V1加入V
以此类推……
(N)找到边(V2,V5),符合条件且最小,将V5加入V,最小生成树构造完成
代码(C++)
虽然是P党,但考虑到Pascal受众较小,我采用C++
代码巨丑,bug一堆,欢迎巨佬吐槽
务必记住,要将A的初值定为正无穷,不然会卡BUG
/*Prim核心代码
HYDcn原创*/
for (int i=2;i<=n;i++)
{
lowcost[i]=a[i][1];//将与V1(或任意一点)有关的边存入lowcost(与各点最小权值)
}
for (int i=1;i<n;i++)
{
minval=1000000;//初始化最小值为正无穷
for (int j=1;j<=n;j++)
{
if (lowcost[j]>0&&lowcost[j]<minval)//如果当前权值不为0(即未连接过)且更小
{
k=j;//记录当前点
minval=lowcost[j];//将最小值存入
}
}
ans+=minval;//统计最小生成树最小权值和
lowcost[k]=0;//标记该点
for (int j=1;j<=n;j++)
{
if (lowcost[j]>0&&lowcost[j]>a[k][j])//由于U集合点增加,需更新与各点最小权值边
{
lowcost[j]=a[k][j];
}
}
}
输入
7 9
1 2 28
1 6 10
2 3 16
2 7 14
3 4 12
4 5 22
4 7 18
5 6 25
5 7 24
输出
99(即权值和)
算法对比
Prim和Kruskal都是最小生成树算法
据说Prim算法适用于稠密图 Kruskal适用于稀疏图
不知道你们信不信,反正我是不信,因为我被亲身卡过
(QAQ算法歧视)
Prim:O(N^2)
Kruskal:O(M log M)
也就是说,只有图稠密得边数M近乎爆满(N^2)时,Prim才略优于Kruskal
Kruskal在绝大部分情况下不会卡,而Prim很容易被卡
能用Kruskal还是尽量用吧
原文:https://www.cnblogs.com/HYDcn666/p/prim.html