1.
问题描述:
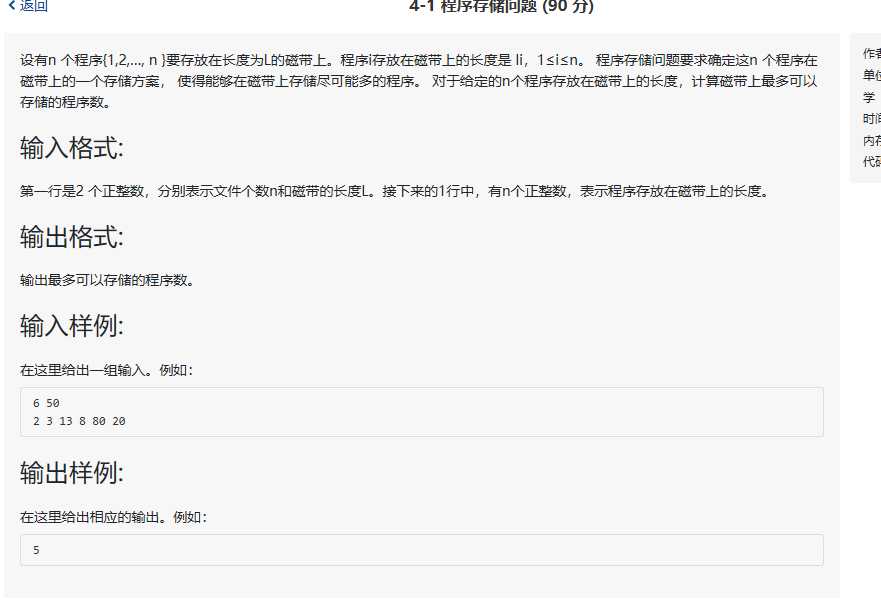
贪心策略:将程序大小从小到大排序,用总内存去从小到大分配,到不能分配为止,即为最大的可分配程序数。
反证法:如果不从最小的开始分配,假设第一个分配大小为P1(Pmin<=P1<=Pmax),总空间为sum,则Pmin可以替换为P1,而且省下了P1-Pmin的空间,这些空间可以分配给其他内存,则分配的策略中,一定有最小的一个程序Pmin,则此时的问题就变成了总空间为sum-Pmin,然后给n-1个程序分配空间,求最大的分配数。则又变成了前面的一个问题。
代码如下:
时间复杂度:输入为O(n),sort排序O(nlogn), 最后分配程序O(n),总的来说是:O(nlogn)
空间复杂度为:O(n)
2.心得体会:
第一题没有什么难度,卡在第二题,第二题一开始的贪心策略以为是【将这个整数中最大数一个个去掉,就可以得到按原序排列的最小数】,然而这个想法是有漏洞的,当遇到大数在后面的时候,如142,148,这样得出来的结果并不是最小的数,所以应该换一个贪心策略,下标从0开始,找到前面的数大于后面的数,就把它删掉,把后面的数往前移,以此类推,找到最小的那个数。最大的收获就是知道了第二题的一种贪心想法,然后组队编程容易漏洞,没错!
原文:https://www.cnblogs.com/wmlcn/p/11874090.html