对于线性可分或者线性近似可分的数据集, 线性支持向量机可以很好的划分,如图左。但是,对于图右的数据集呢?很显然, 这个数据集是没有办法用直线分开的。
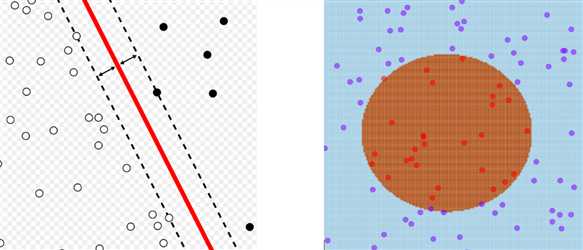
我们的想法是在低维空间中不能线性分割的点集,通过转化为高维空间中的点集时,很有可能变为线性可分的。
插个题外话:看过《三体》的小伙伴们都知道,故事中的主人公进入到四维空间,发现“视野变得十分的开阔”, 进入四维的人,可以直接将三维中的人的内脏取出来,三体中女巫不是靠魔法取出大脑的,而是进入了四维空间, 将活人的大脑取出来了。在三维里面,内脏不还隔着肚皮嘛!但是进入到四维之后,可以做很多三维中看似不可能的事情。所以, 让我们到高维度空间去玩玩吧!
简单的例子, 我们引入了一个映射, 将二维空间映射到三维空间,这样, 看似难以分开的数据集,到高维度里面,只需要简单的一个平面。如下图所示。

定义: 在低维空间中不能线性分割的点集,通过转化为高维空间中的点集时,从而变为线性可分的,这就是核方法。
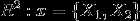 ,我们知道,二维中任意的曲线可以表示成:
,我们知道,二维中任意的曲线可以表示成: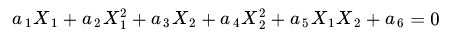
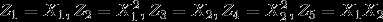 , 得到五维的空间
, 得到五维的空间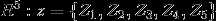
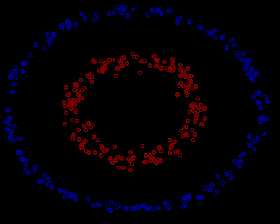
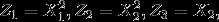 将二维的数据映射到三维中去,得到下图:
将二维的数据映射到三维中去,得到下图: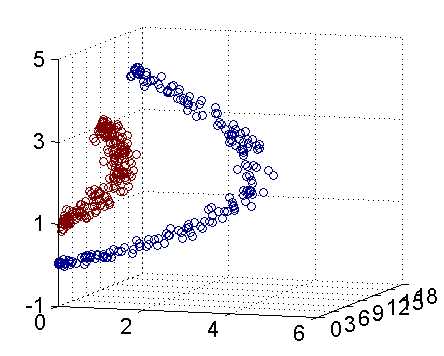
这里用一个简单的例子来说明
设有两个向量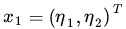 和
和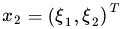
映射定义为: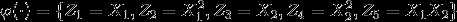
两个向量的映射为:
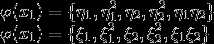
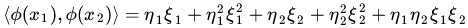
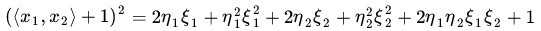
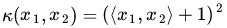
怎么判断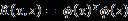 呢?换句话来说,怎么判断我们选的这个核函数有效呢?
呢?换句话来说,怎么判断我们选的这个核函数有效呢?
.

线性核
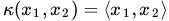
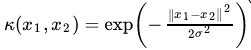
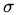 选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果
选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果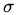 选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。下图所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间:
选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。下图所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间: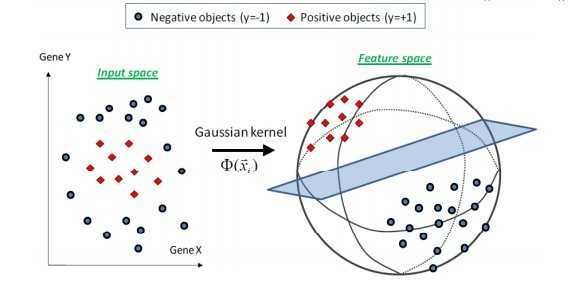
多项式核
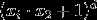
sigmoid核
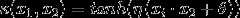

因此,在选用核函数的时候,如果我们对我们的数据有一定的先验知识,就利用先验来选择符合数据分布的核函数;如果不知道的话,通常使用交叉验证的方法,来试用不同的核函数,误差最下的即为效果最好的核函数,或者也可以将多个核函数结合起来,形成混合核函数。在吴恩达的课上,也曾经给出过一系列的选择核函数的方法:
详情参考:SVM几种核优缺点比较
原文:https://www.cnblogs.com/hichens/p/11874645.html