本篇是机器学习小组第二周的学习内容输出。参考的资料包括:
评价分类结果(上):
https://mp.weixin.qq.com/s/Fi13jaEkM5EGjmS7Mm_Bjw
评价分类结果(下):
https://mp.weixin.qq.com/s/elI6-BX-AfKGuVjPPPE0rw
Google Developers for Machine Learning(Classfication)
模型之母:线性回归的评价指标
https://mp.weixin.qq.com/s/BEmMdQd2y1hMu9wT8QYCPg
1.分类中常用的评价指标和使用场景
在第一周kNN的学习中使用了accuracy_score来计算分类的准确率。
1 def accuracy_score(y_true, y_predict): 2 assert y_true.shape[0] != y_predict.shape[0] 3 return sum(y_true == y_predict) / len(y_true)
我们知道二分类的结果非0即1,所以可以通过预测结果和真实结果的差值来衡量预测的准确率。
但单纯依赖准确率会带来一个问题是,即学习链接提到的:预测10000个人是否得癌症,真实情况是9990个人没有癌症。假设预测结果是9978个没得癌症,则预测的准确率是非常高的。这就是所谓的数据有偏的情况,实际上我们希望模型能够尽可能精确的预测人得癌症的准确率,所以这里需要通过引入混淆矩阵(confused-matrix)来解决。
| 预测值0 | 预测值1 | |
| 真实值0 | TN - 9978 | FP - 12 |
| 真实值1 | FN - 2 | TP - 8 |
查准率/精确率:预测值为1,且预测对了的比例。
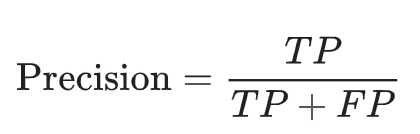
查全率/召回率:所有真实值为1的数据中,预测对了的个数。
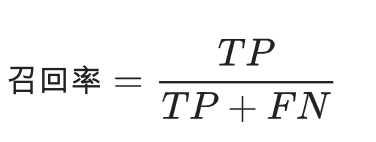
对于这两个指标的理解:首先我们要关注的是模型预测为1的结果;其次,我们希望我们预测的结果尽可能的准(8/(8+12)=40%);同时希望我们预测的结果,能够尽可能的涵盖到真实的情况(8/(8+2)=80%)。所以这是两个互相矛盾的指标。我们可以从分母看出,FP(预测为1)-FN(预测为0)这两个值就是互斥的。
1 def TN(y_true, y_predict): 2 assert len(y_true) == len(y_predict) 3 # 返回预测值和真实值均为0的情况 4 return np.sum(y_true == 0 & y_predict == 0) 5 6 7 def FN(y_true, y_predict): 8 assert len(y_true) == len(y_predict) 9 # 返回真实值为1而预测值为0而的情况 10 return np.sum(y_true == 1 & y_predict == 0) 11 12 13 def FP(y_true, y_predict): 14 assert len(y_true) == len(y_predict) 15 # 返回真实值为0而预测值为1的情况 16 return np.sum(y_true == 0 & y_predict == 1) 17 18 19 def TP(y_true, y_predict): 20 assert len(y_true) == len(y_predict) 21 # 返回真实值和预测值均为1的情况 22 return np.sum(y_true == 1 & y_predict == 1) 23 24 25 def confusion_matrix(y_true, y_predict): 26 return np.array([ 27 [TN(y_true, y_predict), FP(y_true, y_predict)], 28 [FN(y_true, y_predict), TP(y_true, y_predict)] 29 ]) 30 31 32 # for precision 33 def precision_score(y_true, y_predict): 34 tp = TP(y_true, y_predict) 35 fp = FP(y_true, y_predict) 36 try: 37 return tp / (tp + fp) 38 except: 39 return 0.0 40 41 42 # for recall 43 def recall_score(y_true, y_predict): 44 tp = TP(y_true, y_predict) 45 fn = FN(y_true, y_predict) 46 try: 47 return tp / (tp + fn) 48 except: 49 return 0.0
因为查准率和查全率不可调和,而我们希望我们的模型结果可以在两个指标上取得平衡,所以引入了F1 Score这个指标。

ROC曲线(Receiver Operation Characteristic Cureve),描述TPR和FPR之间的关系。x轴是FPR,y轴是TPR。
TPR:预测为1,且预测对了的数量,占真实值为1的数据百分比。其实就是召回率。
FPR: 预测为1,但预测错了的数量,占真实值不为1的数据百分比。
TPR就是所有正例中,有多少被正确地判定为正;FPR是所有负例中,有多少被错误地判定为正。
TPR越大越好,FPR越小越好,但这两个指标通常是矛盾的。为了增大TPR,可以预测更多的样本为正例,与此同时也增加了更多负例被误判为正例的情况。
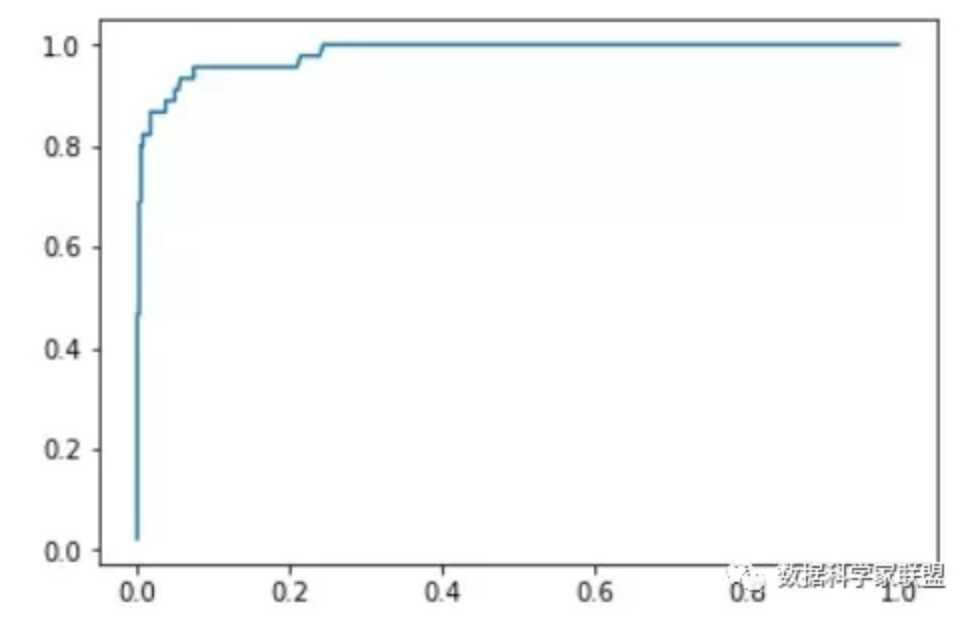
(图片来自于《评价分类结果(下)》)
纵轴是TPR,横轴是FPR。从横轴0.0开始往上,TPR一直在增加(1.0)最好。到0.8时,FPR开始增加。
(TODO)
2.回归(线性回归)中常用的评价指标和使用场景
MSE/MAE/RMSE
(TODO)
3.思考:
(TODO)
原文:https://www.cnblogs.com/favor-dfn/p/11876411.html