算法第四章上机实践报告

一、程序存储问题

1. 实践题目

2. 问题描述

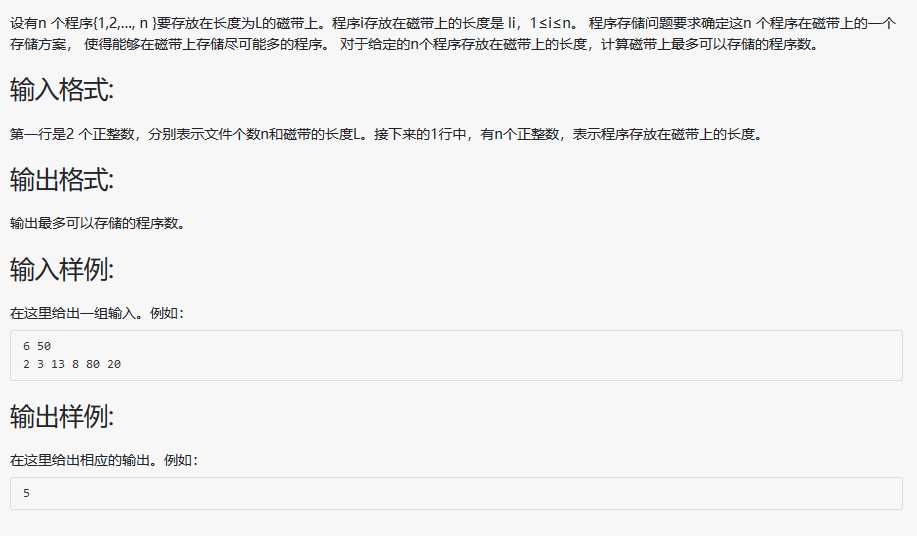
 　　设有n 个程序{1,2,…, n }要存放在长度为L的磁带上。程序i存放在磁带上的长度是 li，1≤i≤n。 程序存储问题要求确定这n 个程序在磁带上的一个存储方案， 使得能够在磁带上存储尽可能多的程序。 对于给定的n个程序存放在磁带上的长度，计算磁带上最多可以存储的程序数。

3. 算法描述（说明你的贪心策略，并且参考会场安排问题，利用反证法证明贪心选择和最优子结构性质）

 　　采用长度最短者优先放的贪心选择策略，可产生该问题的最优解。具体算法如下：

 1 #include <iostream>
 2 #include <algorithm>
 3 using namespace std;
 4 
 5 int main() {
 6     int n, L;
 7     cin >> n >> L;
 8     int l[n];
 9     for (int i = 0; i < n; i++)
10         cin >> l[i];
11     sort(l, l + n);
12     int sum = 0, count = 0;
13     for (int i = 0; i < n; i++) {
14         sum += l[i];
15         if (sum <= L)
16             count++;
17     }
18     cout << count;
19 }

3.1 贪心选择性质：

　　程序按长度从小到大排序，即（x1, x2, ... , xn），x1是长度最小的程序。

3.2 最优子结构性质：

4. 算法时间及空间复杂度分析（要有分析过程）

 　　sort()函数的时间复杂度为O(nlogn)，一个for循环的时间复杂度为O(n)，则整个算法的时间复杂度T(n) = O(nlogn) + O(n)；

　　由于使用的是动态数组，数组所需要的空间会随n的变化而变化，所以空间复杂度为O(n)

5. 心得体会（对本次实践收获及疑惑进行总结）

　　在解决程序存储问题时，我们在对sum进行初始化时，直接给它赋值成了l[0]，这使得代码的可读性降低，后面在老师指出后进行了修改。

　　在处理删数问题时，一开始我们的设想是将字符串进行非降序排序，然后按原顺序输出前面n-k个数，但是提交后只对了例题给的测试数据，后来通过老师给的一组测试数据（样例：13274删除1个数字，如果采用保留全部最小数字的贪心策略，结果是1324，但实际答案应是1274），发现了问题的所在，我们忽略了高位越小则数越小这一点，所以后来我们采用了的贪心选择是删除较大的高位数字，即可以删除字符串中第一个升序数列的最后一个数字，就可以得到最优解。

　　在处理最优合并问题时，我们的贪心选择是：（最差）最长的优先合并，（最优）最短的优先合并。

算法第四章上机实践报告

原文：https://www.cnblogs.com/jewfer-03-08/p/11877191.html