\[ L(\theta^\prime)=p(X|\theta^\prime)=\prod_{i=1}^n p(x_i|\theta^\prime) \]
\[ \pi(\theta|\pmb{x})=\frac{p(\pmb{x}|\theta)\pi(\theta)}{h(\pmb{x},\theta)}=\frac{p(\pmb{x}|\theta)\pi(\theta)}{\int_{\Theta} {p(\pmb{x}|\theta)\pi(\theta)}\rm d\theta} \]
\[ \pi(\theta_i|x)=\frac{p(x|\theta_i)\pi(\theta)}{\sum_{j} {p(x|\theta_j)\pi(\theta_j)}} \]
\[ \pi(\theta)=\begin{cases}1, 0<\theta<1 \0,其他场合 \end{cases} \]
设\(\theta\)是总体分布中的参数(或参数向量),\(\pi(\theta)\)是\(\theta\)的先验密度函数,假如由抽样信息算得的后验密度函数与\(\pi(\theta)\)有相同的函数形式,则称\(\pi(\theta)\)是\(\theta\)的(自然)共轭先验分布。通过这种方式计算得到的后验分布的一些参数可以很好解释。共轭先验分布的选区是由似然函数所含的\(\theta\)因式所决定,即选与似然函数(\(\theta\)的函数)具有相同核的分布作为先验分布。
\[ 先验知识\theta \sim N(\mu,\tau^2) 总体分布x \sim N(\theta,\sigma^2)样本 \overline{x}, \sigma_0^2=\frac{\sigma^2}{n}\后验知识\pi(\theta|\pmb{x}) \sim N(\mu_1,\tau_1^2) \\]
\[ \mu_1=\frac{\frac{\mu}{\tau^2}+\frac{\overline{x}}{\sigma_0^2}}{ \frac{1}{\tau^2}+\frac{1}{\sigma_0^2} } \\ \frac{1}{\tau_1^2}=\frac{1}{\tau^2}+\frac{1}{\sigma_0^2} \]
\[ 先验\theta \sim Be(\alpha,\beta)总体X \sim b(n,\theta)\后验\pi(\theta|\pmb{x}) \sim Be(\alpha+x,\beta+n-x) \]
\[ E(\theta|x)=\frac{\alpha+x}{\alpha+\beta+n}=\frac{n}{\alpha+\beta+n}\frac{x}{n}+\frac{\alpha+\beta}{\alpha+\beta+n}\frac{\alpha}{\alpha+\beta} \Var(\theta|x)\approx \frac1n \frac{x}{n}(1-\frac{x}{n}) \]

在单参数指数族场合,使用共轭先验分布得后验均值一定值于先验均值与样本均值(或样本方差等)之间。
后验分布的计算:由于\(m(x)\)不依赖于\(\theta\),在计算时仅起到正则化因子的作用,\[\pi(\theta|\pmb{x}) \propto p(\pmb{x}|\theta)\pi(\theta)\],其中各因子提取出仅与\(\theta\)有关的称为核。计算时可以略去与\(\theta\)无关的因子。
先验分布的选取,应以合理性作为首要原则
超参数:先验分布中所含的未知参数称为超参数。无信息先验分布一般不含超参数。
多参数模型(实际问题中常有多个未知参数,而一般不关注的参数称为讨厌参数)
条件方法
后验分布是在样本x给定下θ的条件分布,基于后验分布的统计推断就意味着只考虑已出现的数据(样本观察值),而认为未出现的数据与推断无关,这一重要的观点被称为“条件观点“,基于这种观点提出的统计推断方法被称为条件方法。
从后验分布中选用某个特征量作为θ的估计。使后验密度达到最大的值\(\theta_{MG}\)称为最大后验估计;后验分布的中位数\(\theta_{Me}\)称为\(\theta\)的后验中位数估计;后验分布的期望值\(\theta_{E}\)称为θ的后验期望估计,这三个估计也都称为θ的贝叶斯估计,记为\(\theta_{B}\),在不引起混乱时也记为\(\theta_{0}\)。实际中,一般采用后验期望估计作为贝叶斯估计。

对于区间估计问题,贝叶斯方法具有处理方便和含义清晰的优点,而经典方法寻求的置信区间常受到批评。
可信区间:
设参数\(\theta\)的后验分布为\(\pi(\theta|x)\),给定样本x和概率α (0<α<1),若存在这样两个统计量\(\theta_U\) \(\theta_L\),使得\(P(\theta_L \le \theta \le \theta_U | x) > 1-\alpha\),则称区间[\(\theta_U\) ,\(\theta_L\) ]为\(\theta\)的可信水平为\(1-\alpha\)的贝叶斯可信区间,即参数\(\theta\)的\(1-\alpha\)的可信区间。仿照经典方法,可以得到\(1-\alpha\)的单侧可信下限和\(1-\alpha\)的单侧可信上限。
最大后验密度(HPD)可信区间
区间长度最短,并把具有最大后验密度的点都包含在区间内,而区间外的点上的后验密度函数值不超过区间内的后验密度函数值
假设检验
获得后验分布后,计算两个假设H0与H1的后验概率,然后比较两者的大小,即观察后验概率比\(\alpha_0/\alpha_1\),从中选择最大概率的一方;但当两者相接近时需要进一步抽样或搜集信息。此种方法可推广到三个及以上的假设状况。
贝叶斯因子,既依赖于样本数据x,还依赖于先验分布\(\pi\),这会减弱先验的影响,突出数据的影响;贝叶斯因子体现了数据支持某假设的程度。贝叶斯因子对样本信息变化的反应是灵敏的,而对先验信息变化的反应是迟钝的。
\[
B^\pi(x)=\frac{\text{后验机会比}}{\text{先验机会比}}=\frac{\alpha_0/\alpha_1}{\pi_0/\pi_1}=\frac{\alpha_0\pi_1}{\pi_0\alpha_1}
\]
简单对简单(参数假设为特定值)
\[ B^\pi(x)=\frac{\alpha_0\pi_1}{\pi_0\alpha_1}=\frac{p(x|\theta_0)}{p(x|\theta_1)} \]
复杂对复杂(参数假设为特定区间,使用g(θ)约束θ的范围表示θ的分布情况,特别的取两个区间θ的极大似然估计代替g(θ)的加权结果可以得到经典统计的似然比统计量)
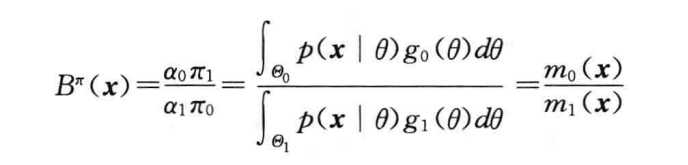
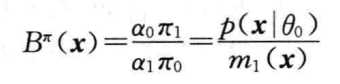
? 由于此类情况的贝叶斯因子计算简单,可以使用其计算得到θ的后验分布:
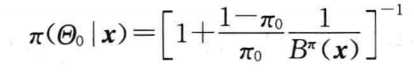
以上的三种可以拓展到多重假设问题,PS: 针对现实问题,需要根据已知的信息和分布特定,设定总体分布和先验函数。
预测(对随机变量未来观察值做出统计推断,一般先获得变量分布,再取期望、中位数、众数、一定区间等作为预测值)预测值的方差一般大于实测值的方差。
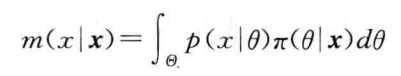
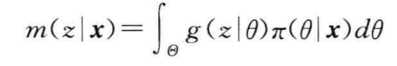
似然原理 当x的样本值给出时,似然函数为\(L(\theta)=p(x|\theta)=\prod_{i=1}^n p(x_i|\theta)\) 这是一个关于θ的函数,使似然函数在参数空间取最值的\(\hat{\theta}\)称为最大似然估计。

参考书籍:《贝叶斯统计》
参考答案:https://wenku.baidu.com/view/4643d9c180eb6294dd886c66?fromShare=1
更多内容,欢迎关注公众号 豆豆的笔记本
原文:https://www.cnblogs.com/joeat1/p/11884806.html