二分查找java实现

　　二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

　　二分查找思路非常简单，由粗暴的遍历查找改为了将元素排序后不断的进行折半查找，将搜索的时间复杂度由O（N）降到了O（log₂N）。

　　二分查找的思路与二叉查找树的查找过程完全相同，我们将一个经过排序的数组看做一棵平衡的二叉查找树，那么数组的中点便是树的根节点。折半后的中点是下一层子树的根节点，以此类推。我们通过不断的判断目标值与各树根节点的值的大小来决定下一步查找根节点的左子树还是右子树。

　　在实现时，我们可以维护两个指针left和right，指针之间的范围便是我们的查找范围。查找过程如下：

　　首先判断边界条件，left位置的值与right位置的值是否包含目标值，若包含则查找结束；

　　　　通过left与right的位置找到当前范围的中点mid，即mid的值为(left+right)/2；

　　　　如果mid的值便是target的值，查找结束；

　　　　如果left与right已经是相邻的元素，那么证明数组中没有目标值，查找结束；

　　　　如果目标值大于mid则在mid、right间继续查找，即将mid的值赋予left；

　　　　反之在left与mid间继续查找，即将mid的值赋予right；

　　left指针与right指针的移动如下图所示（例子为在目标数组中查找20）：

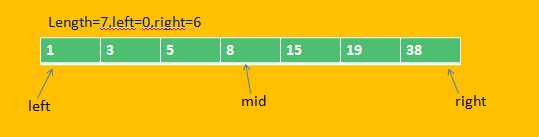
　　大于mid则在mid、right间继续查找，即将上次查找的mid值赋予left：

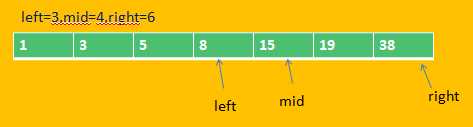
 　　同上：

 　　同上：

 　　此时left与right相邻，仍未找到目标值，即数组中没有包含目标值。

 　　代码实现如下，值得注意的是，(left+right)/2有可能会造成整数溢出问题，我们可改写为left+(right-left)/2来防止该问题，下面看代码：

 public final int searchInsert(int[] nums, int target) {
        if(nums==null){
            throw new NullPointerException("目标数组为空!");
        }
        int left=0;
        int right=nums.length-1;
        //边界条件
        if(target>nums[right]){return right+1;}
        if(target<nums[left]){return 0;}
        while(true){
            //计算当前中点
            int mid=left+(right-left)/2;
            //找到目标值
            if(target==nums[mid]){
                return mid;
            }
            //未找到目标值但终止循环
            if(right==left+1){
                return right;
            }
            if(target>nums[mid]){
                left=mid;
            }
            if(target<nums[mid]){
                right=mid;
            }
        }

二分查找java实现

原文：https://www.cnblogs.com/niuyourou/p/11885123.html