笔者在另一篇文章中对贝叶斯网的理论部分进行了总结,在本文中,我们重点关注其在具体场景里的应用。
我们知道,朴素贝叶斯分类器和Logistic regression模型都是产生概率估计来代替硬性的分类。对于每个类值,它们都是估计某个实例属于这个类的概率。
实际上,大多数其他机器学习分类器都可以转化为产生这类信息的模型,例如:
概率估计经常比简单的预测更为有用,它们可以对所做的预测结果进行排名,使期望成本达到最小化。
本质上说,概率预测属于生成式模型的一种特殊形式,基于概率的分类模型所估计的是给定其他属性值时类属性值的条件概率分布。理想情况下,分类模型是用一种简洁易懂的形式来表达这个条件分布。
由此看来,朴素贝叶斯分类器、Logistic回归模型、决策树等只是用不同的方法表达条件概率的分布。当然,它们的表达能力有所差别:
总结来说,传统的概率预测模型有如下几个困局与挑战:
解决这一问题的一路研究分支是抛弃概率预测模型,转而研究和使用预测精度更高的判别式模型,例如:
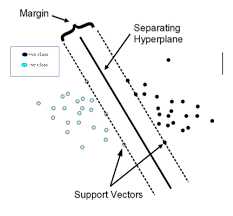
另一方面,另一路研究分支是引入更为复杂的概率模型,从统计理论方法上出发,采用图形方式来表达概率分布,这个结构被称为贝叶斯网络(Bayesian network)。画出的图形就像是节点的网络图,每个节点代表一个属性,节点间用有向线段连接,但不能形成环,即一个有向无环图(directed acyclic graph)。
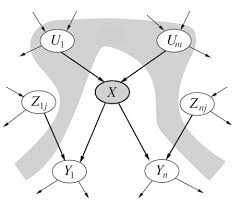
我们接下来讨论关于贝叶斯网算法的具体应用方面的知识点。
贝叶斯网的主要任务是对随机变量间的条件概率依赖关系(conditional independence relationships among the variables)进行建模,它的底层思想是:
贝叶斯网通过条件概率因子分解的形式来抽象表达这种关系,即:

每个局部概率分布(local distribution)都有自己的参数集ΘXi,? ΘX 远小于 Θ,这源自于贝叶斯网的局部条件独立性。
如下图所示,A、S、E、O、R、T 分别代表着6个不同的随机变量,其对应的贝叶斯网关系可能如下:
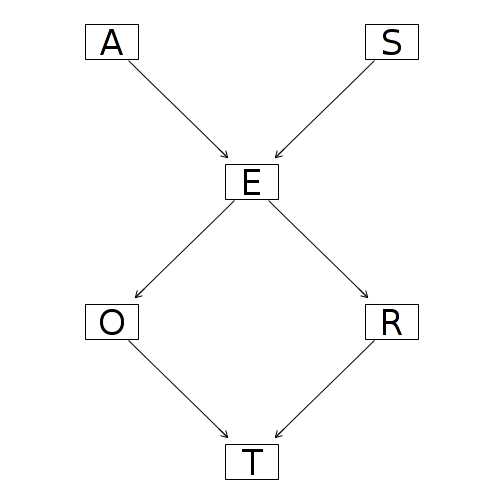
贝叶斯网关系图

因子分解式
Relevant Link:
《数据挖掘 实用机器学习工具与技术》Ian H.Witten Eibe Frank,Mark A.Hall
在讨论贝叶斯网的建模和训练之前,笔者希望先通过一个具体的例子,来给大家建立一个对贝叶斯网的感性认识。
一是因为在训练中涉及到的一些技术和概念和预测是共享的,二是通过对预测的讨论,将贝叶斯网这个看起来有些抽象的概念拉回到贝叶斯公式、朴素贝叶斯分类器、马尔柯夫链的理解框架之内,有助于我们建立一些直观的认知和加速理解。
下图是关于一个天气数据的贝叶斯网实例,
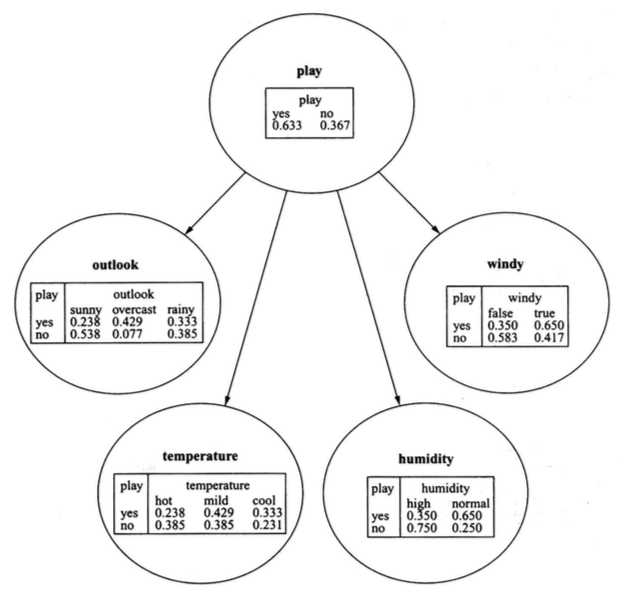
一个天气数据的简单贝叶斯网络实例
可以看到, 图中的数据包含了4个属性:outlook、temperature、humidity、windy,以及类属性play,分别用结点表示。
从这个例子我们可以看到,描述一个贝叶斯网络,由两部分组成:
在继续讨论概率预测之前,我们继续来看一个稍微复杂一些的例子,上面的例子可能还不能非常明显地表达出贝叶斯网的概念。
我们来看一个和上一小节相同问题的,但是情况更为复杂的网络例子,
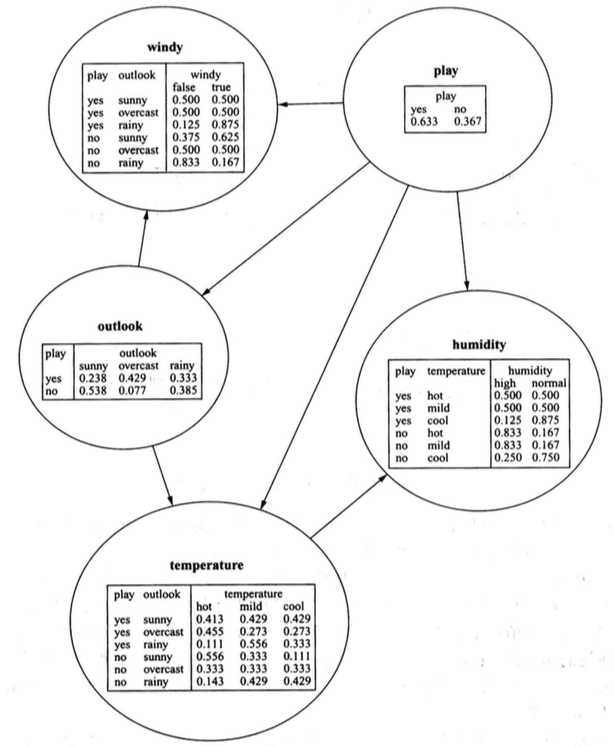
天气数据的另一个贝叶斯网络
在这个例子中,“windy”、“temperature”、“humidity”有两个父节点。在这3个节点中,每个父节点都会在属性概率表格中产生一列,以联合条件概率的形式逐行排列,右边的列数等于节点属性的属性值数量。
假设我们现在已经确定了某个数据集对应的贝叶斯网的结构和节点属性概率,接下来的问题是怎么利用这些表来预测某个实例的每个类值的概率呢?答案很简单,依然是我们熟悉的贝叶斯链式法则。
实例的每个属性都有确定的属性值,对网络中的每个结点,根据父节点属性值找到相应的行,并查看该行结点属性值的概率,然后将这些概率相乘,得到的累乘结果就是我们要的实例类值概率。
例如,考虑这样一个实例:【play=?outlook=rainy,temperature=cool,humidity=high,windy=true】,现在需要计算play=no的概率。
所以有:
显然,这不是最终的答案,最终的概率之和应该为1,而现在0.0025+0.0077显然不等于1,那么问题出在哪呢?
实际上,它们是 Pr[play=no,E] 和 Pr[play=yes,E] 的联合概率,其中 E 是指由这个实例的属性值所给出的所有证据。联合概率既度量实例的属性值出现在 E 中的可能性,也度量相应的类值。只有穷尽了包括类属性在内的所有可能的属性值组合空间时,它们的和才为1。显然这个例子不属于这种情况。
上面这么说可能还有些抽象,通俗地说就是,Pr[play=no,E] 和 Pr[play=yes,E] 只代表了2个概率链条,图中还有其他的概率链条,例如:
【play=?outlook=overcast,temperature=cool,humidity=high,windy=true】
outlook属性值的不同,使概率链条进入了另一个分布空间
给出了实例类值概率的计算过程和结果后,接下来我们继续追问一个问题。凭什么可以将这些概率相乘呢?
在马尔柯夫链式公式中我们很好理解,条件概率是以因果链条的关系依次展开的,如下图:

一阶马尔科夫链公式
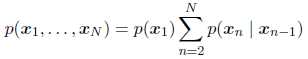
每个节点都只考虑其邻接父节点对其的影响
现在到了一个图结构中,还能依然遵循这种链式展开思想吗?答案是肯定的!!
实际上,贝叶斯网是比马尔柯夫链更泛化的一种通用框架,马尔柯夫链是贝叶斯网在马尔柯夫假设前提下的一种特殊形式。
以上面天气的例子为例,按照标准贝叶斯链式分解法则,实例类值 P(play=?,E) 的全概率链式分解公式如下:
这是一个标准的因果递归链分解公式。基于这种分解方式得到的是一个完全的网状结构。
但是,根据贝叶斯网条件概率分布(CPD: conditional probability distribution)独立性法则,网络中存在很多结点间是无相关性关系的,也就是说很多结点间是不存在有向边的。这种现象称之为贝叶斯网的紧凑性。
基于这种紧凑性原理,标准的贝叶斯链式分解法则可以通过约简得到一个更紧凑的表示,上面全概率公式可以改写为:
和上一小节的实例类值公式进行一些对比会发现,在公式形式上是相同的,
可以看到,首先,贝叶斯全概率链式分解定理是累乘合理性的理论基础。同时,通过局部条件独立性原理,繁杂的全概率公式可以得到化简,得到一个相对精简的概率累乘式。
这在贝叶斯网理论体系中称之为因子分解式。
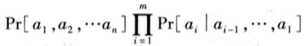
a1, a2,.. 代表图中每个节点,Par(ai)就表示除了ai以外的所有节点。公式中的逗号表示“与”的关系
乘积步骤的有效性有一个前提假设,就是给定每个父节点的属性值,知道任何其他非子孙结点的属性值并不能使该结点的各个可能的属性值所对应的概率发生变化,也就是所谓的局部独立性假设(local independencies)。
换句话说,就是非子孙结点并不能提供任何多于父节点所能提供有关该结点属性值的信息,这点可以表示为下式:
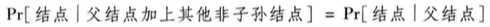
给定父节点,每个结点对于它的祖父节点、层祖父节点、以及其他非子孙结点都是条件独立的,在这种情况下,实例类值的累乘式是有效的。乘积步骤遵循概率论中的链式规则。
有一点值得注意的,这个分解表达式对于任何一种属性排列都是成立的,因为贝叶斯网是一个无环图,可以将网络结点进行排列,将上式重写为:
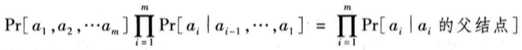
这就是上一小节应用的乘积规则。
对比一下这个章节和上个章节的两个贝叶斯网络,我们会发现它们是完全不同的。
假设贝叶斯网中的有向边代表的是因果关系,这是一个直觉上的判断。但是要谨慎!!
在本章的例子中,play属性值会使outlook的某个具体值所对应的期望值提高,但事实上两者没有因果关系,实际上两者之间存在的是相关关系,相关性不等于因果性。
为某个领域某件贝叶斯网络的数据分析师们总是期望有向边能够表达因果性,然而,当使用机器学习技术(统计方法)从因果结构未知的数据中推导模型时,所能做的只是根据从数据中观察到的相关性建立网络,而从相关性推导因果关系的风险总是很大的。
Relevant Link:
https://www.cnblogs.com/LittleHann/p/11683607.html#_label3_2_1_1
通过前面的讨论我们知道,决定一个贝叶斯网的两个核心因素分别是:
其中网络结点连接结构是最关键的因素,因为网络结点间连接方式决定了贝叶斯网概率链式分解公式可以如何约简。确定了概率链式分解公式之后,很容易基于贝叶斯定理反向计算出每个结点的条件概率分布。
整个贝叶斯过程如下图所示:

我们首先来讨论如何基于数据集训练确定贝叶斯网络的结构。
在贝叶斯网中,实例的每个属性(包括类别)都有一个结点。学习网络结构等于是在可能的有向边空间中进行搜索,对每组连接方案对应的条件概率表进行评估,并计算结果网络基于某个数据集的对数似然,以此作为对网络质量的度量。

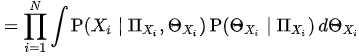
要实现网络结构的学习,需要两个基本组件:
假设网络结构(即所有的边)是已知的,很容易估计条件概率列表中的概率分布,只要计算训练数据中对应属性值组合的相对频率即可。同时为了避免出现零概率,一般使用一个常量来初始化分布的初始先验概率(概率平滑)。
同时为了避免累乘中出现算数下溢(累乘结果数字变得非常小),以至于不能较好地反映质量,因此我们使用概率对数的总和来代替原先的乘积,最终的结果就是给定数据时,整个网络的对数似然。有一点需要注意,如果直接基于对数似然率对训练数据进行了最大化,增加更多的有向边总是会获得更好的结果,造成最终网络过度拟合。有很多方法可以缓解这个问题,包括:
有两个常用的度量方法可用于评估网络质量:
这两个表达式的结果都是正数,因此优化目标就是使它们的得分最小化。
如果使用适当的评分度量,搜寻一个好的网络结构就成功了一半。我们知道,网络中某个实例的概率是所有条件概率表中单个概率的乘积,所以数据集的总体概率是把所有的实例概率再累乘起来得到。
由于乘积运算中的项是可以互换的,所以这个乘积可以重写为把同属于一个表的各个系数组合在一起的形式。这同样适合使用对数似然用求和运算代替乘积运算。这意味着似然的优化可以在网络的每个结点中分别进行(分段优化)。
我们可以通过增加或去除其他结点指向正在进行优化的结点的边来完成,唯一的限制就只不可引入环。如果使用局部评分度量(如AIC或MDL)方案来代替朴素的对数似然,这个方法也同样生效,因为惩罚项会被分裂成多个组成部分,每个结点各一个,而且每个结点可以进行独立的优化。
基于以上关于优化过程的讨论,就引出了接下来要讲的“有向边连接空间的搜索策略”,贝叶斯网络结点支持分段优化的这种特性,使得我们可以应用启发式的优化算法,对网络结构进行启发式地探索。
各种贝叶斯网络学习算法的不同之处在于它们在网络结构空间的搜索方式不同,本小节我们讨论一些经典的算法思想,把握其发展的脉络。
K2算法是一个简单而快速的启发式算法,简要描述如下:
由于只考虑起始于前面已经处理过的节点的边,并且顺序是固定的,所以这个过程不会产生环。
特别地,朴素贝叶斯分类器是这样一种网络,它的边是由类属性指向其他每个属性。当为分类建立网络时,使用这种网络作为搜寻起点是很有帮助的。可以使用K2方案来实现,强制把类属性列为序列中的第一个属性并合理地设定初始边。
另一个潜在的有用技巧就是有效的利用结点的马尔可夫毯(Markov blanket)特性。一个结点的马尔可夫毯包含该结点的父节点、子结点、子结点的父节点。
可以证明结点与它的马尔可夫毯内的所有其他结点都是条件独立的。因此,如果一个结点不包括在类属性的马尔可夫毯内,那么该结点所代表的属性与分类就是毫无关系的。
反过来,如果K2发现一个网络结构没有将某个相关属性包含类属性的马尔可夫毯内,或者可以增加一条边来纠正这个缺点。一个简单的方法就是增加一条从这个属性结点指向类结点(或相反)的边,这要取决于哪种方向可以避免环,同时还取决于网络结构质量评估函数的判定结果。
不进行结点排序,而是直接采取贪心策略增加或去除任意一对结点间的边,是一个更为周全却较慢的K2版本。再进一步就是要同时考虑反转现有的边。
需要明白的是,使用任何的贪心算法,结果网络都只能代表某个评分函数局部最大值,并不一定就是全局最优值。这是启发式搜索的原生弊端。
通常建议采用不同的随机初始值多次运行算法,还可以使用如模拟退火、禁忌搜索、或遗传算法等更为复杂的优化策略。
一种启发式最短路径搜索算法。
Relevant Link:
https://www.google.com.hk/search?newwindow=1&safe=strict&hl=zh-CN&sxsrf=ACYBGNQ6fvIClIfRwRyXUasIvDRpeZpjEQ%3A1574044570225&source=hp&ei=mgPSXYb0Cs6AtgX18K6QBg&q=mmhc.r+&oq=mmhc.r+&gs_l=psy-ab.3...1738.1738..1925...0.0..0.0.0.......0....2j1..gws-wiz.&ved=0ahUKEwiGqd373PLlAhVOgK0KHXW4C2IQ4dUDCAY&uact=5
通过上一章节的讨论我们知道,通过启发式的结构搜索,以及基于使每个实例的联合概率Pr[a1,a2,...,an]最大化的评分度量,我们可以得到一个局部最优的网络结构。
确定了结构后,问题就转变了一个常规的贝叶斯条件概率估计的运算,这通过简单的统计概率论知识可以做到。
得到结点概率分布如下图所示:

然而有一点要注意的是,在分类问题中,真正要最大化的是在给定其他属性值的情况下类的条件概率,换句话说就是条件似然。
但不幸的是,对贝叶斯网络的列表中所需要的最大条件似然概率估计没有解析解(启发式局部搜索没有全局解析解)。因此,在实际的情况中,网络的训练使用标准最大似然估计,而对某个具体的网络结构则采用条件似然来评估。
Relevant Link:
《数据挖掘 实用机器学习工具与技术》Ian H.Witten Eibe Frank,Mark A.Hall
贝叶斯网推断本身也属于贝叶斯推断范畴内的一种,通常来说,我们讨论和使用较多的是下列两种形式:
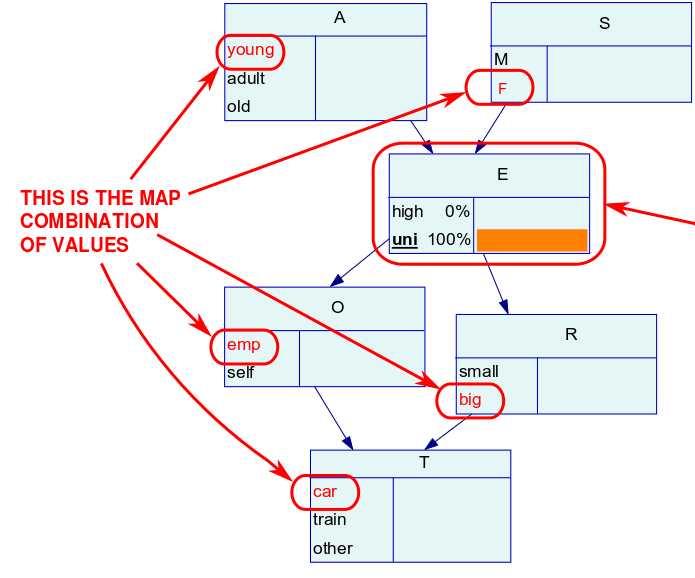
我们以一个离散随机变量组成的贝叶斯网为例,其DAG图如下:
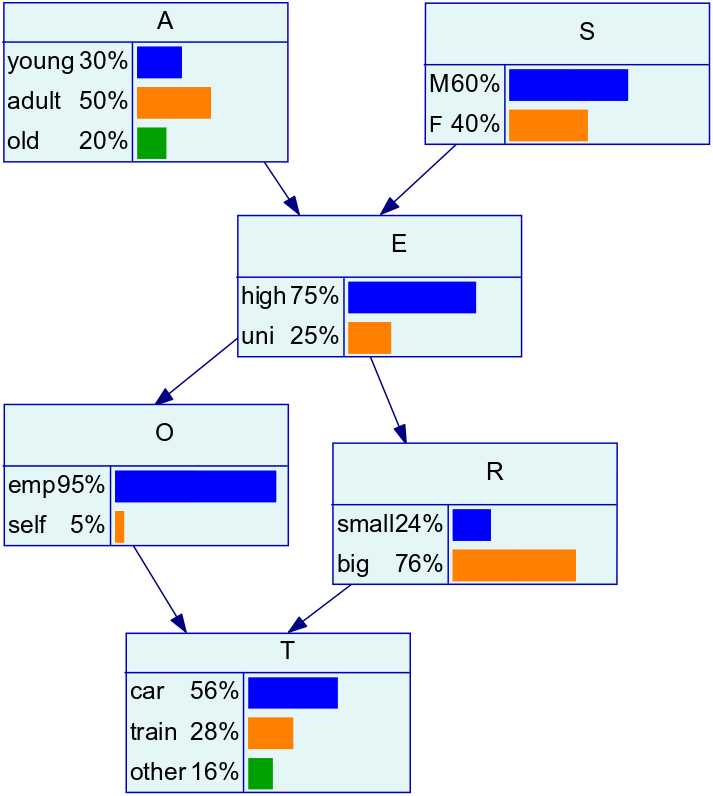
推断过程示意图如下:
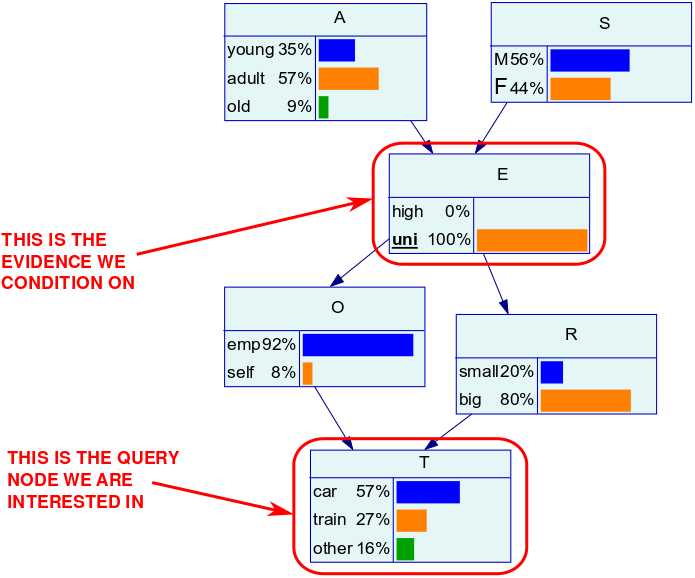
换句话说,贝叶斯网MAP查询就是在已有证据的前提条件下,推断网络中余下结点最有可能的后验概率组合,从这个角度来看,贝叶斯网MAP是在进行分类预测任务。
Relevant Link:
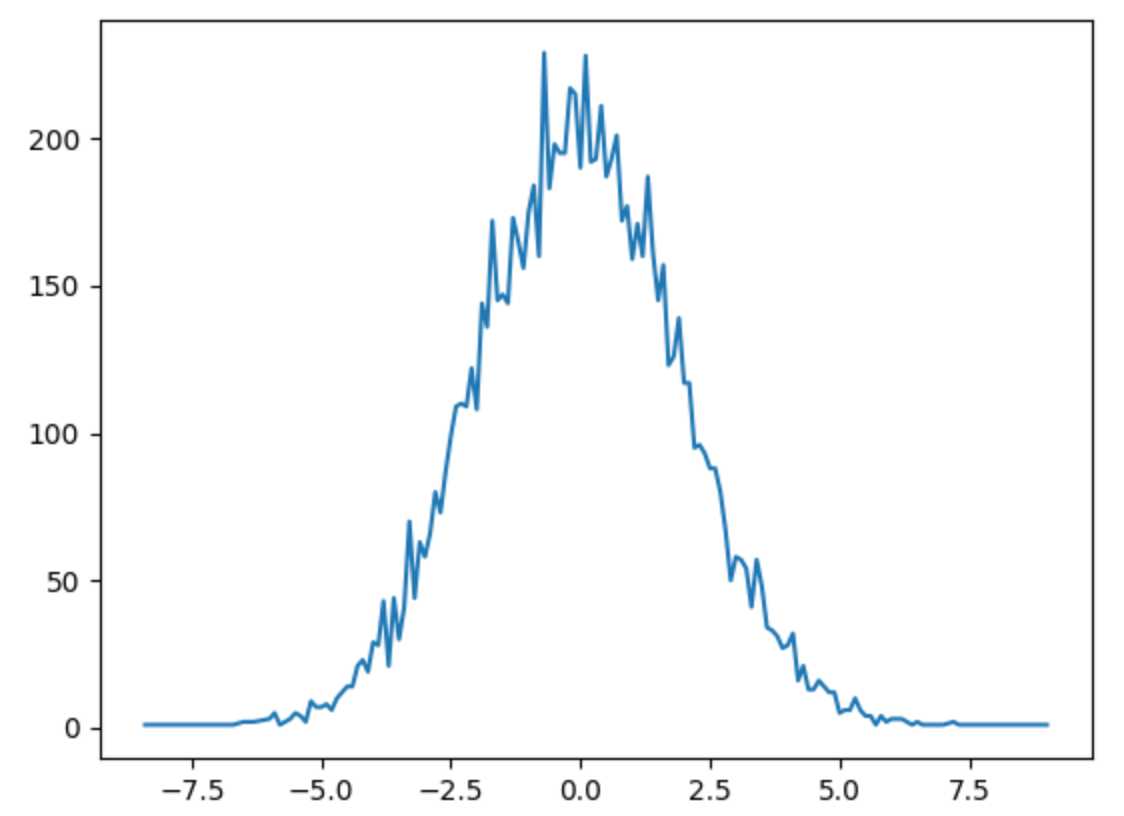
# -*- coding:utf-8 -*- from pomegranate import * import pygraphviz as pgv import matplotlib.pyplot as plt def plot_xy(x, y): plt.plot(x, y) plt.show() if __name__ == ‘__main__‘: mu, sig = 0, 2 model = NormalDistribution(mu, sig) x_y = {} for i in range(9999): x = float("%.1f" % model.sample()) if x_y.has_key(x): x_y[x] += 1 else: x_y[x] = 1 x_y = sorted(x_y.items(), key=lambda d: d[0]) print x_y x = [i[0] for i in x_y] y = [i[1] for i in x_y] print x print y plot_xy(x, y)
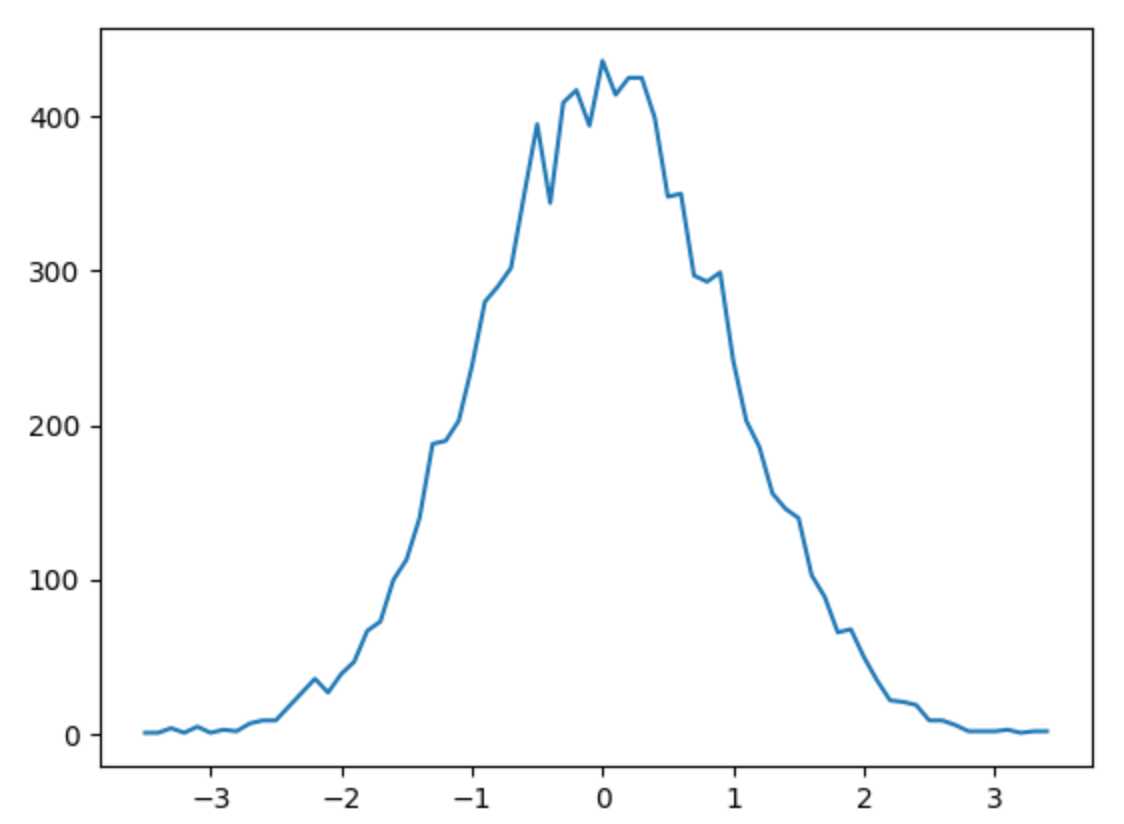
# -*- coding:utf-8 -*- from pomegranate import * import pygraphviz as pgv import matplotlib.pyplot as plt import numpy as np def plot_xy(x, y): plt.plot(x, y) plt.show() def generate_data(): X = np.random.normal(0, 1, 100) model = NormalDistribution.from_samples(X) return model def generate_xy_plot(model): x_y = {} for i in range(9999): x = float("%.1f" % model.sample()) if x_y.has_key(x): x_y[x] += 1 else: x_y[x] = 1 x_y = sorted(x_y.items(), key=lambda d: d[0]) print x_y x = [i[0] for i in x_y] y = [i[1] for i in x_y] print x print y return x,y if __name__ == ‘__main__‘: model = generate_data() x, y = generate_xy_plot(model) plot_xy(x, y)
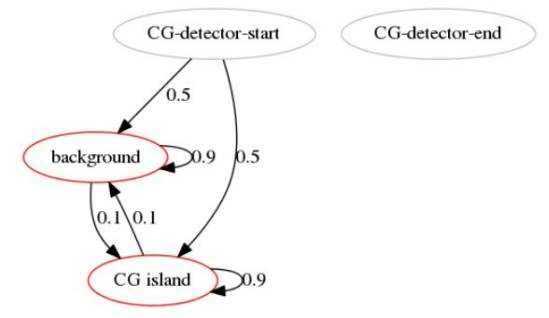
# -*- coding:utf-8 -*- from pomegranate import * import pygraphviz as pgv import matplotlib.pyplot as plt import numpy as np if __name__ == ‘__main__‘: d1 = DiscreteDistribution({ ‘A‘: 0.25, ‘C‘: 0.25, ‘G‘: 0.25, ‘T‘: 0.25 }) d2 = DiscreteDistribution({ ‘A‘: 0.10, ‘C‘: 0.40, ‘G‘: 0.40, ‘T‘: 0.10 }) s1 = State(d1, name="background") # 隐状态 s2 = State(d2, name="CG island") # 显状态 hmm = HiddenMarkovModel("CG-detector") hmm.add_states(s1, s2) # 状态概率转移矩阵 hmm.add_transition(hmm.start, s1, 0.5) hmm.add_transition(hmm.start, s2, 0.5) # 隐状态和显状态的概率发射矩阵 hmm.add_transition(s1, s1, 0.9) hmm.add_transition(s1, s2, 0.1) hmm.add_transition(s2, s1, 0.1) hmm.add_transition(s2, s2, 0.9) hmm.bake() # observed_sequence = "GACTACGACTCGCGCTCGCGCGACGCGCTCGACATCATCGACACGACACTC" print "how likely the sequence happen: ", hmm.log_probability(list(observed_sequence)) print "the corresponding hidden state sequence: ", hmm.predict(list(observed_sequence))
![]()
关于”Monty Hall problem“的背景描述可以参阅这篇文章, 这里对:
这3个随机变量分别抽象为3个结点,根据题意分析,每个结点内部的条件概率分布都是已知的,所以我们可以直接跳过结构学习和概率学习这2个环节,直接进行建模。
# -*- coding:utf-8 -*- from pomegranate import * import pygraphviz as pgv import matplotlib.pyplot as plt import numpy as np if __name__ == ‘__main__‘: guest = DiscreteDistribution({‘A‘: 1. / 3, ‘B‘: 1. / 3, ‘C‘: 1. / 3}) prize = DiscreteDistribution({‘A‘: 1. / 3, ‘B‘: 1. / 3, ‘C‘: 1. / 3}) monty = ConditionalProbabilityTable( [[‘A‘, ‘A‘, ‘A‘, 0.0], [‘A‘, ‘A‘, ‘B‘, 0.5], [‘A‘, ‘A‘, ‘C‘, 0.5], [‘A‘, ‘B‘, ‘A‘, 0.0], [‘A‘, ‘B‘, ‘B‘, 0.0], [‘A‘, ‘B‘, ‘C‘, 1.0], [‘A‘, ‘C‘, ‘A‘, 0.0], [‘A‘, ‘C‘, ‘B‘, 1.0], [‘A‘, ‘C‘, ‘C‘, 0.0], [‘B‘, ‘A‘, ‘A‘, 0.0], [‘B‘, ‘A‘, ‘B‘, 0.0], [‘B‘, ‘A‘, ‘C‘, 1.0], [‘B‘, ‘B‘, ‘A‘, 0.5], [‘B‘, ‘B‘, ‘B‘, 0.0], [‘B‘, ‘B‘, ‘C‘, 0.5], [‘B‘, ‘C‘, ‘A‘, 1.0], [‘B‘, ‘C‘, ‘B‘, 0.0], [‘B‘, ‘C‘, ‘C‘, 0.0], [‘C‘, ‘A‘, ‘A‘, 0.0], [‘C‘, ‘A‘, ‘B‘, 1.0], [‘C‘, ‘A‘, ‘C‘, 0.0], [‘C‘, ‘B‘, ‘A‘, 1.0], [‘C‘, ‘B‘, ‘B‘, 0.0], [‘C‘, ‘B‘, ‘C‘, 0.0], [‘C‘, ‘C‘, ‘A‘, 0.5], [‘C‘, ‘C‘, ‘B‘, 0.5], [‘C‘, ‘C‘, ‘C‘, 0.0]], [guest, prize]) s1 = Node(guest, name="guest") s2 = Node(prize, name="prize") s3 = Node(monty, name="monty") model = BayesianNetwork("Monty Hall Problem") model.add_states(s1, s2, s3) model.add_edge(s1, s3) model.add_edge(s2, s3) model.bake() model.plot()
基于训练得到的贝叶斯网模型进行预测任务,就是沿着DAG中结点的连接拓朴,将所涉及结点的条件概率进行累乘。
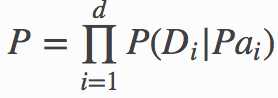
以上小节Monty Hall问题为例,累乘的对象就是:
# -*- coding:utf-8 -*- from pomegranate import * import pygraphviz as pgv import matplotlib.pyplot as plt import numpy as np if __name__ == ‘__main__‘: guest = DiscreteDistribution({‘A‘: 1. / 3, ‘B‘: 1. / 3, ‘C‘: 1. / 3}) prize = DiscreteDistribution({‘A‘: 1. / 3, ‘B‘: 1. / 3, ‘C‘: 1. / 3}) monty = ConditionalProbabilityTable( [[‘A‘, ‘A‘, ‘A‘, 0.0], [‘A‘, ‘A‘, ‘B‘, 0.5], [‘A‘, ‘A‘, ‘C‘, 0.5], [‘A‘, ‘B‘, ‘A‘, 0.0], [‘A‘, ‘B‘, ‘B‘, 0.0], [‘A‘, ‘B‘, ‘C‘, 1.0], [‘A‘, ‘C‘, ‘A‘, 0.0], [‘A‘, ‘C‘, ‘B‘, 1.0], [‘A‘, ‘C‘, ‘C‘, 0.0], [‘B‘, ‘A‘, ‘A‘, 0.0], [‘B‘, ‘A‘, ‘B‘, 0.0], [‘B‘, ‘A‘, ‘C‘, 1.0], [‘B‘, ‘B‘, ‘A‘, 0.5], [‘B‘, ‘B‘, ‘B‘, 0.0], [‘B‘, ‘B‘, ‘C‘, 0.5], [‘B‘, ‘C‘, ‘A‘, 1.0], [‘B‘, ‘C‘, ‘B‘, 0.0], [‘B‘, ‘C‘, ‘C‘, 0.0], [‘C‘, ‘A‘, ‘A‘, 0.0], [‘C‘, ‘A‘, ‘B‘, 1.0], [‘C‘, ‘A‘, ‘C‘, 0.0], [‘C‘, ‘B‘, ‘A‘, 1.0], [‘C‘, ‘B‘, ‘B‘, 0.0], [‘C‘, ‘B‘, ‘C‘, 0.0], [‘C‘, ‘C‘, ‘A‘, 0.5], [‘C‘, ‘C‘, ‘B‘, 0.5], [‘C‘, ‘C‘, ‘C‘, 0.0]], [guest, prize]) s1 = Node(guest, name="guest") s2 = Node(prize, name="prize") s3 = Node(monty, name="monty") model = BayesianNetwork("Monty Hall Problem") model.add_states(s1, s2, s3) model.add_edge(s1, s3) model.add_edge(s2, s3) model.bake() print model.probability([[‘A‘, ‘A‘, ‘A‘], [‘A‘, ‘A‘, ‘B‘], [‘C‘, ‘C‘, ‘B‘]])
![]()
Relevant Link:
https://www.ctolib.com/jmschrei-pomegranate.html https://pomegranate.readthedocs.io/en/latest/whats_new.html https://blog.laisky.com/p/pygraphviz/ http://www.sohu.com/a/150274125_505915 https://github.com/jmschrei/pomegranate/blob/master/docs/BayesianNetwork.rst https://pomegranate.readthedocs.io/en/latest/faq.html https://pomegranate.readthedocs.io/en/latest/BayesianNetwork.html
Relevant Link:
http://www.bnlearn.com/examples/ http://www.bnlearn.com/examples/useR19-tutorial/ http://www.bnlearn.com/book-crc/
基于贝叶斯网(Bayes Netword)图模型的应用实践初探
原文:https://www.cnblogs.com/LittleHann/p/11855323.html