树链剖分

时间：2019-11-18 23:51:55 阅读：132 评论：0 收藏：0 [点我收藏+]

洛谷·[模板]树链剖分

写在前面

首先，在学树链剖分之前最好先把 LCA、树形DP、DFS序这三个知识点学了
emm还有必备的链式前向星、线段树也要先学了。

如果这三个知识点没掌握好的话，树链剖分难以理解也是当然的。

树链剖分

树链剖分就是对一棵树分成几条链，把树形变为线性，减少处理难度
需要处理的问题：

将树从x到y结点最短路径上所有节点的值都加上z
求树从x到y结点最短路径上所有节点的值之和
将以x为根节点的子树内所有节点值都加上z
求以x为根节点的子树内所有节点值之和

概念

重儿子：对于每一个非叶子节点，它的儿子中以那个儿子为根的子树节点数最大的儿子为该节点的重儿子 (Ps: 感谢@shzr大佬指出我此句话的表达不严谨qwq, 已修改)
轻儿子：对于每一个非叶子节点，它的儿子中非重儿子的剩下所有儿子即为轻儿子
叶子节点没有重儿子也没有轻儿子（因为它没有儿子。。）
重边：一个父亲连接他的重儿子的边称为重边 //原写法：连接任意两个重儿子的边叫做重边
轻边：剩下的即为轻边
重链：相邻重边连起来的连接一条重儿子的链叫重链
- 对于叶子节点，若其为轻儿子，则有一条以自己为起点的长度为1的链
- 每一条重链以轻儿子为起点

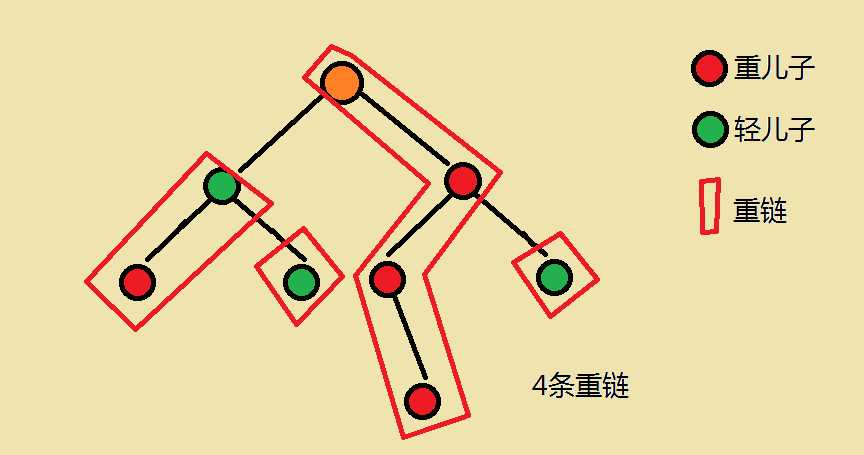
技术分享图片

dfs1()

这个dfs要处理几件事情：

标记每个点的深度dep[]
标记每个点的父亲fa[]
标记每个非叶子节点的子树大小(含它自己)
标记每个非叶子节点的重儿子编号son[]

inline void dfs1(int x,int f,int deep){//x当前节点，f父亲，deep深度 
    dep[x]=deep;//标记每个点的深度 
    fa[x]=f;//标记每个点的父亲 
    siz[x]=1;//标记每个非叶子节点的子树大小 
    int maxson=-1;//记录重儿子的儿子数 
    for(Rint i=beg[x];i;i=nex[i]){
        int y=to[i];
        if(y==f)continue;//若为父亲则continue 
        dfs1(y,x,deep+1);//dfs其儿子 
        siz[x]+=siz[y];//把它的儿子数加到它身上 
        if(siz[y]>maxson)son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号 
    }
}//变量解释见最下面

dfs2()

这个dfs2也要预处理几件事情

标记每个点的新编号
赋值每个点的初始值到新编号上
处理每个点所在链的顶端
处理每条链

顺序：先处理重儿子再处理轻儿子，理由后面说

inline void dfs2(int x,int topf){//x当前节点，topf当前链的最顶端的节点 
    id[x]=++cnt;//标记每个点的新编号 
    wt[cnt]=w[x];//把每个点的初始值赋到新编号上来 
    top[x]=topf;//这个点所在链的顶端 
    if(!son[x])return;//如果没有儿子则返回 
    dfs2(son[x],topf);//按先处理重儿子，再处理轻儿子的顺序递归处理 
    for(Rint i=beg[x];i;i=nex[i]){
        int y=to[i];
        if(y==fa[x]||y==son[x])continue;
        dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链 
    }
}//变量解释见最下面

处理问题

Attention 重要的来了！！！
前面说到dfs2的顺序是先处理重儿子再处理轻儿子
我们来模拟一下：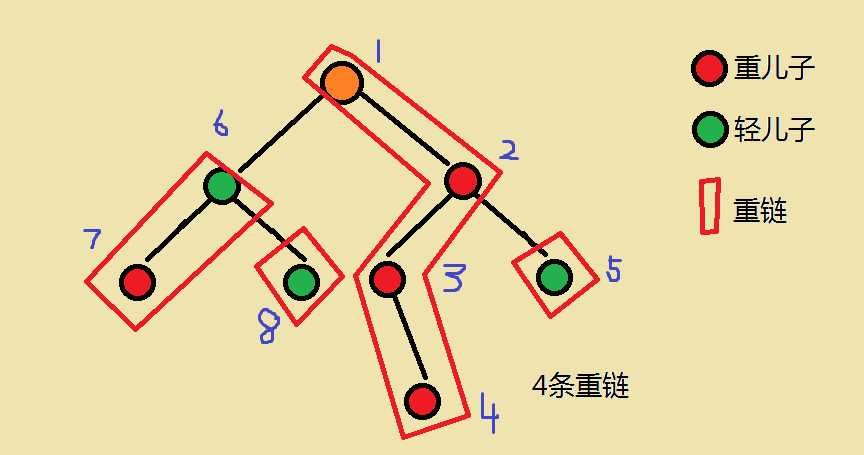
技术分享图片

因为顺序是先重再轻，所以每一条重链的新编号是连续的
因为是dfs，所以每一个子树的新编号也是连续的

现在回顾一下我们要处理的问题

处理任意两点间路径上的点权和
处理一点及其子树的点权和
修改任意两点间路径上的点权
修改一点及其子树的点权

1、当我们要处理任意两点间路径时：
设所在链顶端的深度更深的那个点为x点

ans加上x点到x所在链顶端这一段区间的点权和
把x跳到x所在链顶端的那个点的上面一个点

不停执行这两个步骤，直到两个点处于一条链上，这时再加上此时两个点的区间和即可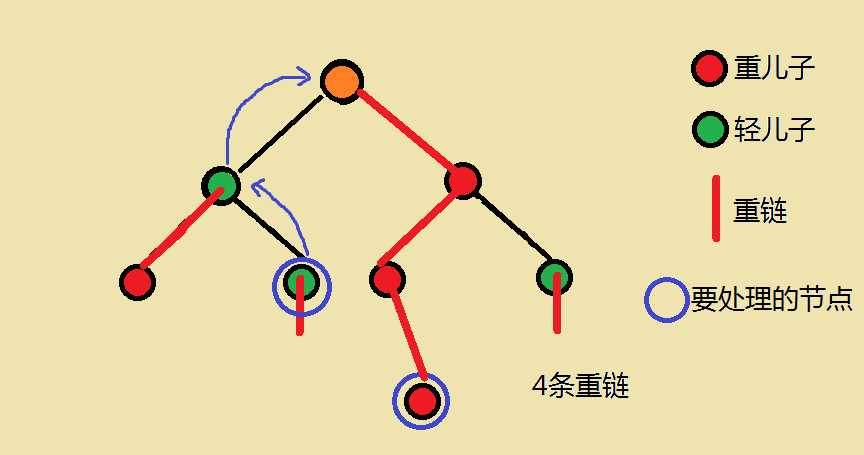
技术分享图片

这时我们注意到，我们所要处理的所有区间均为连续编号(新编号)，于是想到线段树，用线段树处理连续编号区间和
每次查询时间复杂度为

inline int qRange(int x,int y){
    int ans=0;
    while(top[x]!=top[y]){//当两个点不在同一条链上 
        if(dep[top[x]]<dep[top[y]])swap(x,y);//把x点改为所在链顶端的深度更深的那个点
        res=0;
        query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
        ans+=res;
        ans%=mod;//按题意取模 
        x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
    }
    //直到两个点处于一条链上
    if(dep[x]>dep[y])swap(x,y);//把x点深度更深的那个点
    res=0;
    query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可
    ans+=res;
    return ans%mod;
}//变量解释见最下面

2、处理一点及其子树的点权和：
想到记录了每个非叶子节点的子树大小(含它自己)，并且每个子树的新编号都是连续的
于是直接线段树区间查询即可
时间复杂度为

inline int qSon(int x){
    res=0;
    query(1,1,n,id[x],id[x]+siz[x]-1);//子树区间右端点为id[x]+siz[x]-1 
    return res;
}

当然，区间修改就和区间查询一样的啦~~

inline void updRange(int x,int y,int k){
    k%=mod;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        update(1,1,n,id[top[x]],id[x],k);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    update(1,1,n,id[x],id[y],k);
}

inline void updSon(int x,int k){
    update(1,1,n,id[x],id[x]+siz[x]-1,k);
}//变量解释见最下面

建树

既然前面说到要用线段树，那么按题意建树就可以啦！
不过，建树这一步当然是在处理问题之前哦~

AC代码：

  1 #include<algorithm>
  2 #include<iostream>
  3 #include<cstdlib>
  4 #include<cstring>
  5 #include<cstdio>
  6 #define Rint register int
  7 #define mem(a,b) memset(a,(b),sizeof(a))
  8 #define Temp template<typename T>
  9 using namespace std;
 10 typedef long long LL;
 11 Temp inline void read(T &x){
 12     x=0;T w=1,ch=getchar();
 13     while(!isdigit(ch)&&ch!=‘-‘)ch=getchar();
 14     if(ch==‘-‘)w=-1,ch=getchar();
 15     while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^‘0‘),ch=getchar();
 16     x=x*w;
 17 }
 18 
 19 #define mid ((l+r)>>1)
 20 #define lson rt<<1,l,mid
 21 #define rson rt<<1|1,mid+1,r
 22 #define len (r-l+1)
 23 
 24 const int maxn=200000+10;
 25 int n,m,r,mod;
 26 //见题意 
 27 int e,beg[maxn],nex[maxn],to[maxn],w[maxn],wt[maxn];
 28 //链式前向星数组，w[]、wt[]初始点权数组 
 29 int a[maxn<<2],laz[maxn<<2];
 30 //线段树数组、lazy操作 
 31 int son[maxn],id[maxn],fa[maxn],cnt,dep[maxn],siz[maxn],top[maxn]; 
 32 //son[]重儿子编号,id[]新编号,fa[]父亲节点,cnt dfs_clock/dfs序,dep[]深度,siz[]子树大小,top[]当前链顶端节点 
 33 int res=0;
 34 //查询答案 
 35 
 36 inline void add(int x,int y){//链式前向星加边 
 37     to[++e]=y;
 38     nex[e]=beg[x];
 39     beg[x]=e;
 40 }
 41 //-------------------------------------- 以下为线段树 
 42 inline void pushdown(int rt,int lenn){
 43     laz[rt<<1]+=laz[rt];
 44     laz[rt<<1|1]+=laz[rt];
 45     a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
 46     a[rt<<1|1]+=laz[rt]*(lenn>>1);
 47     a[rt<<1]%=mod;
 48     a[rt<<1|1]%=mod;
 49     laz[rt]=0;
 50 }
 51 
 52 inline void build(int rt,int l,int r){
 53     if(l==r){
 54         a[rt]=wt[l];
 55         if(a[rt]>mod)a[rt]%=mod;
 56         return;
 57     }
 58     build(lson);
 59     build(rson);
 60     a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
 61 }
 62 
 63 inline void query(int rt,int l,int r,int L,int R){
 64     if(L<=l&&r<=R){res+=a[rt];res%=mod;return;}
 65     else{
 66         if(laz[rt])pushdown(rt,len);
 67         if(L<=mid)query(lson,L,R);
 68         if(R>mid)query(rson,L,R);
 69     }
 70 }
 71 
 72 inline void update(int rt,int l,int r,int L,int R,int k){
 73     if(L<=l&&r<=R){
 74         laz[rt]+=k;
 75         a[rt]+=k*len;
 76     }
 77     else{
 78         if(laz[rt])pushdown(rt,len);
 79         if(L<=mid)update(lson,L,R,k);
 80         if(R>mid)update(rson,L,R,k);
 81         a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
 82     }
 83 }
 84 //---------------------------------以上为线段树 
 85 inline int qRange(int x,int y){
 86     int ans=0;
 87     while(top[x]!=top[y]){//当两个点不在同一条链上 
 88         if(dep[top[x]]<dep[top[y]])swap(x,y);//把x点改为所在链顶端的深度更深的那个点
 89         res=0;
 90         query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
 91         ans+=res;
 92         ans%=mod;//按题意取模 
 93         x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
 94     }
 95     //直到两个点处于一条链上
 96     if(dep[x]>dep[y])swap(x,y);//把x点深度更深的那个点
 97     res=0;
 98     query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可
 99     ans+=res;
100     return ans%mod;
101 }
102 
103 inline void updRange(int x,int y,int k){//同上 
104     k%=mod;
105     while(top[x]!=top[y]){
106         if(dep[top[x]]<dep[top[y]])swap(x,y);
107         update(1,1,n,id[top[x]],id[x],k);
108         x=fa[top[x]];
109     }
110     if(dep[x]>dep[y])swap(x,y);
111     update(1,1,n,id[x],id[y],k);
112 }
113 
114 inline int qSon(int x){
115     res=0;
116     query(1,1,n,id[x],id[x]+siz[x]-1);//子树区间右端点为id[x]+siz[x]-1 
117     return res;
118 }
119 
120 inline void updSon(int x,int k){//同上 
121     update(1,1,n,id[x],id[x]+siz[x]-1,k);
122 }
123 
124 inline void dfs1(int x,int f,int deep){//x当前节点，f父亲，deep深度 
125     dep[x]=deep;//标记每个点的深度 
126     fa[x]=f;//标记每个点的父亲 
127     siz[x]=1;//标记每个非叶子节点的子树大小 
128     int maxson=-1;//记录重儿子的儿子数 
129     for(Rint i=beg[x];i;i=nex[i]){
130         int y=to[i];
131         if(y==f)continue;//若为父亲则continue 
132         dfs1(y,x,deep+1);//dfs其儿子 
133         siz[x]+=siz[y];//把它的儿子数加到它身上 
134         if(siz[y]>maxson)son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号 
135     }
136 }
137 
138 inline void dfs2(int x,int topf){//x当前节点，topf当前链的最顶端的节点 
139     id[x]=++cnt;//标记每个点的新编号 
140     wt[cnt]=w[x];//把每个点的初始值赋到新编号上来 
141     top[x]=topf;//这个点所在链的顶端 
142     if(!son[x])return;//如果没有儿子则返回 
143     dfs2(son[x],topf);//按先处理重儿子，再处理轻儿子的顺序递归处理 
144     for(Rint i=beg[x];i;i=nex[i]){
145         int y=to[i];
146         if(y==fa[x]||y==son[x])continue;
147         dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链 
148     }
149 }
150 
151 int main(){
152     read(n);read(m);read(r);read(mod);
153     for(Rint i=1;i<=n;i++)read(w[i]);
154     for(Rint i=1;i<n;i++){
155         int a,b;
156         read(a);read(b);
157         add(a,b);add(b,a);
158     }
159     dfs1(r,0,1);
160     dfs2(r,r);
161     build(1,1,n);
162     while(m--){
163         int k,x,y,z;
164         read(k);
165         if(k==1){
166             read(x);read(y);read(z);
167             updRange(x,y,z);
168         }
169         else if(k==2){
170             read(x);read(y);
171             printf("%d\n",qRange(x,y));
172         }
173         else if(k==3){
174             read(x);read(y);
175             updSon(x,y);
176         }
177         else{
178             read(x);
179             printf("%d\n",qSon(x));
180         }
181     }
182 }

树链剖分

原文：https://www.cnblogs.com/pangbi/p/11886417.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)