目录
1
标定好的真实数据(标准答案)
机器学习里经常出现ground truth这个词,能否准确解释一下? - 非理的回答 - 知乎
在有监督学习中,数据是有标注的,以\((x, t)\)的形式出现,其中\(x\)是输入数据,\(t\)是标注。正确的
$t$标注是 ground truth。
参考:
准确率(Accuracy), 精确率(Precision), 召回率(Recall)和F1-Measure
首先引入基本概念:TP、FP、FN、TN
| 预测情况 | 相关(Relevant),正类 | 无关(NonRelevant),负类 |
|---|---|---|
| 正类 | true positives (TP 正类判定为正类) | false positives (FP 负类判定为正类) |
| 负类 | false negatives (FN 正类判定为负类) | true negatives (TN 负类判定为负类) |
说明:
TP:T 判断正确,P 判断为正类
FP:F 判断错误,P 判断为正类,实际为负类
FN:F 判断错误,N 判断为负类,实际为正类
TN:T 判断正确,N 判断为负类
Accuracy:准确率,对于给定的测试数据集,分类器正确分类的样本数与总样本数之比。
公式表示如下:
\[ A=\frac{TP+TN}{TP+FP+FN+TN} \]
对于 Precision 和 Recall 来说都是针对正类来考虑的,就是说我正类找的对不对、全不全。
Precision:精确率/查准率,在所有判断为正类的结果(TP、FP)中,判断正确(TP)所占的比例。
通俗理解:找的对不对,我找到的所有正类中对的比例
公示表示如下:
\[ P=\frac{TP}{TP+FP} \]
Recall:召回率/查全率,对于实际为正类(TP,FN)的所有内容中,判断正确(TP)所占的比例。
通俗理解:找的全不全,所有的正类被正确找到的比例
公式表示如下:
\[ R=\frac{TP}{TP+FN} \]
查准率:查的准不准,看看所有判断为正例中判断对的比例
查全率:查的全不全,看看所有的正例中被正确查到的比例
参考:

A:检索到的,相关的 (搜到的也想要的)
B:检索到的,但是不相关的 (搜到的但没用的)
C:未检索到的,但却是相关的 (没搜到,然而实际上想要的)
D:未检索到的,也不相关的 (没搜到也没用的)
---
参考:argmin ,argmax函数
参考:arg max - wikipedia
arg max: arguments of the maxima,最大值对应的点集
arg min: arguments of the minima,最小值对应的点集
max:最大值
min:最小值
举例如下:
\[
{\displaystyle {\underset {x}{\operatorname {arg\,max} }}\,f(x):=\{x\mid \forall y:f(y)\leq f(x)\}.}
\]
\[
{\displaystyle {\underset {x}{\operatorname {arg\,max} }}\,(1-|x|)=\{0\}}.
\]
\[
{\displaystyle {\underset {x}{\operatorname {arg\,max} }}\,\left(4x^{2}-x^{4}\right)=\left\{-{\sqrt {2}},{\sqrt {2}}\right\}}
\]
\[
{\displaystyle {\underset {x}{\operatorname {max} }}\,\left(4x^{2}-x^{4}\right)=\{4\}}
\]
\[
{\displaystyle {\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,(x(10-x))=5}
\]
\[
{\displaystyle {\underset {x\in [0,4\pi ]}{\operatorname {arg\,max} }}\,\cos(x)=\{0,2\pi ,4\pi \}}
\]
\[
{\displaystyle {\underset {x}{\operatorname {arg\,min} }}\,f(x):=\{x\mid x\in S\wedge \forall y\in S:f(y)\geq f(x)\}}
\]
参考:LaTeX输入单个点、横向多个点、竖向多个点、斜向多个点
行向量用逗号分隔
列向量用分号分隔
在教学书里面一般是按照列向量来表示。
行向量:\(\vec{y} = (y_1,y_2,y_3,...,y_m)\)
列向量:\(\vec{y} = (y_1;y_2;y_3;...;y_m)\)
行向量表示如下:
\[
\vec{y}=
\left[
\begin{matrix}
y_1 & y_2 & y_3 & \cdots & y_m
\end{matrix}
\right]
=
\left[
\begin{matrix}
y_1 , y_2 , y_3 , \cdots , y_m
\end{matrix}
\right]
\]
列向量表示如下:
$$
\vec{y}=
\left[
\begin{matrix}
y_1 & y_2 & y_3 & \cdots & y_m
\end{matrix}
\right]^T
=
\left[
\begin{matrix}
y_1 , y_2 , y_3 , \cdots , y_m
\end{matrix}
\right]^T
=
\left[
\begin{matrix}
y_1 \
y_2 \
y_3 \
\vdots \
y_m
\end{matrix}
\right]
=
\left[
\begin{matrix}
y_1 ; y_2 ; y_3 ; \cdots ; y_m
\end{matrix}
\right]
$$
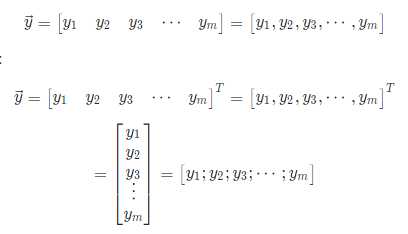
\(\theta\) 的一个估计量记为\(\widehat{\theta}\)。对于 Wikipedia 里面的公式,显示是以图片的形式显示,但是复制的时候可以将其 LaTeX 源码复制出来。
原文:https://www.cnblogs.com/alex-bn-lee/p/11887765.html