遗传算法
1、基本思想
2、算法原理
3、代码实现
4、结果截图
5、总结
1·基本思想
吸取两个算法的优点,优缺互补,克服两个算法的缺点,利用了遗传算法的快速时间效率,优于蚂蚁算法的时间效率。并且求解精度效率优于遗传算法。这样就提高了两个算法结合的算法时间效率和求解精度。
2、算法原理
这个算法的原理是先利用遗传算法的快速性、全局收敛性和随机性求出结果,结果产生有关问题的初始信息素分布,遗传算法执行完在运用蚁群算法,在一定初始信息素分布的情况下,充分利用蚁群算法并行性、正反馈性、求解精度效率高的特点。
3、代码实现
%main
clear;
clc;
%%%%%%%%%%%%%%%输入参数%%%%%%%%
N=50; %%城市的个数
M=100; %%种群的个数
ITER=500; %%迭代次数
%C_old=C;
m=2; %%适应值归一化淘汰加速指数
Pc=0.8; %%交叉概率
Pmutation=0.05; %%变异概率
%%生成城市的坐标
pos=randn(N,2);
%%生成城市之间距离矩阵
D=zeros(N,N);
for i=1:N
for j=i+1:N
dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
D(i,j)=dis^(0.5);
D(j,i)=D(i,j);
end
end
%%生成初始群体
popm=zeros(M,N);
for i=1:M
popm(i,:)=randperm(N);%随机排列,比如[2 4 5 6 1 3]
end
%%随机选择一个种群
R=popm(1,:);
figure(1);
scatter(pos(:,1),pos(:,2),‘rx‘);%画出所有城市坐标
axis([-3 3 -3 3]);
figure(2);
plot_route(pos,R); %%画出初始种群对应各城市之间的连线
axis([-3 3 -3 3]);
%%初始化种群及其适应函数
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M%计算每个染色体对应的总长度
len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);%最大回路
minlen=min(len);%最小回路
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);%找到最小值的下标,赋值为rr
R=popm(rr(1,1),:);%提取该染色体,赋值为R
for i=1:N
fprintf(‘%d ‘,R(i));%把R顺序打印出来
end
fprintf(‘\n‘);
fitness=fitness/sum(fitness);
distance_min=zeros(ITER+1,1); %%各次迭代的最小的种群的路径总长
nn=M;
iter=0;
while iter<=ITER
fprintf(‘迭代第%d次\n‘,iter);
%%选择操作
p=fitness./sum(fitness);
q=cumsum(p);%累加
for i=1:(M-1)
len_1(i,1)=myLength(D,popm(i,:));
r=rand;
tmp=find(r<=q);
popm_sel(i,:)=popm(tmp(1),:);
end
[fmax,indmax]=max(fitness);%求当代最佳个体
popm_sel(M,:)=popm(indmax,:);
%%交叉操作
nnper=randperm(M);
% A=popm_sel(nnper(1),:);
% B=popm_sel(nnper(2),:);
%%
for i=1:M*Pc*0.5
A=popm_sel(nnper(i),:);
B=popm_sel(nnper(i+1),:);
[A,B]=cross(A,B);
% popm_sel(nnper(1),:)=A;
% popm_sel(nnper(2),:)=B;
popm_sel(nnper(i),:)=A;
popm_sel(nnper(i+1),:)=B;
end
%%变异操作
for i=1:M
pick=rand;
while pick==0
pick=rand;
end
if pick<=Pmutation
popm_sel(i,:)=Mutation(popm_sel(i,:));
end
end
%%求适应度函数
NN=size(popm_sel,1);
len=zeros(NN,1);
for i=1:NN
len(i,1)=myLength(D,popm_sel(i,:));
end
maxlen=max(len);
minlen=min(len);
distance_min(iter+1,1)=minlen;
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
fprintf(‘minlen=%d\n‘,minlen);
R=popm_sel(rr(1,1),:);
for i=1:N
fprintf(‘%d ‘,R(i));
end
fprintf(‘\n‘);
popm=[];
popm=popm_sel;
iter=iter+1;
%pause(1);
end
%end of while
figure(3)
plot_route(pos,R);
axis([-3 3 -3 3]);
figure(4)
plot(distance_min);
%交叉操作函数 cross.m
function [A,B]=cross(A,B)
L=length(A);
if L<10
W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
W=ceil(L/10)+8;
else
W=floor(L/10)+8;
end
%%W为需要交叉的位数
p=unidrnd(L-W+1);%随机产生一个交叉位置
%fprintf(‘p=%d ‘,p);%交叉位置
for i=1:W
x=find(A==B(1,p+i-1));
y=find(B==A(1,p+i-1));
[A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
[A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end
end
%连点画图函数 plot_route.m
function plot_route(a,R)
scatter(a(:,1),a(:,2),‘rx‘);
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
hold on;
for i=2:length(R)
x0=a(R(i-1),1);
y0=a(R(i-1),2);
x1=a(R(i),1);
y1=a(R(i),2);
xx=[x0,x1];
yy=[y0,y1];
plot(xx,yy);
hold on;
end
end
%染色体的路程代价函数 mylength.m
function len=myLength(D,p)%p是一个排列
[N,NN]=size(D);
len=D(p(1,N),p(1,1));
for i=1:(N-1)
len=len+D(p(1,i),p(1,i+1));
end
end
%变异函数 Mutation.m
function a=Mutation(A)
index1=0;index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf(‘index1=%d ‘,index1);
%fprintf(‘index2=%d ‘,index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;
end
%适应度函数fit.m,每次迭代都要计算每个染色体在本种群内部的优先级别,类似归一化参数。越大约好!
function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i=1:length(len)
fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end
%对调函数 exchange.m
function [x,y]=exchange(x,y)
temp=x;
x=y;
y=temp;
end
4、结果截图
图1 图2
图3 图4
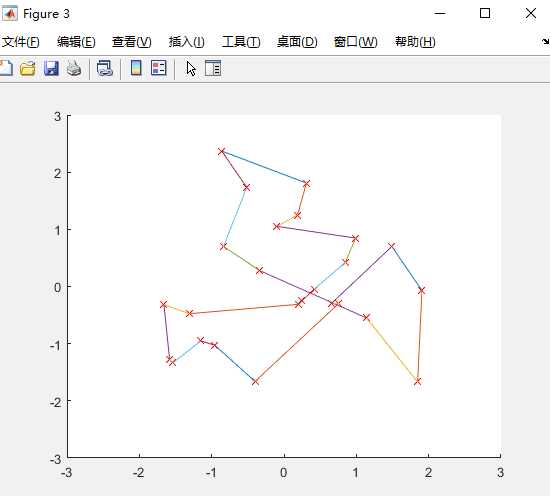
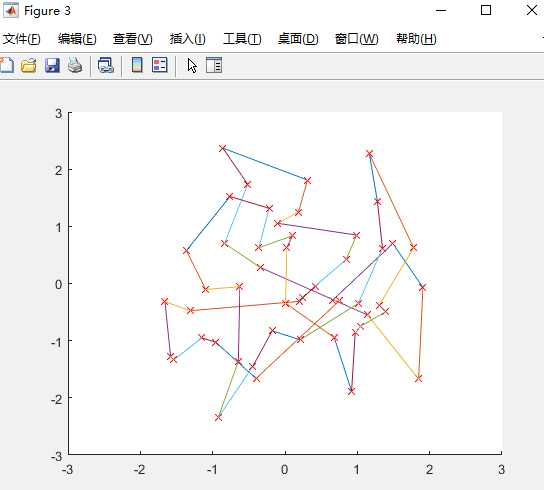
图5 图6
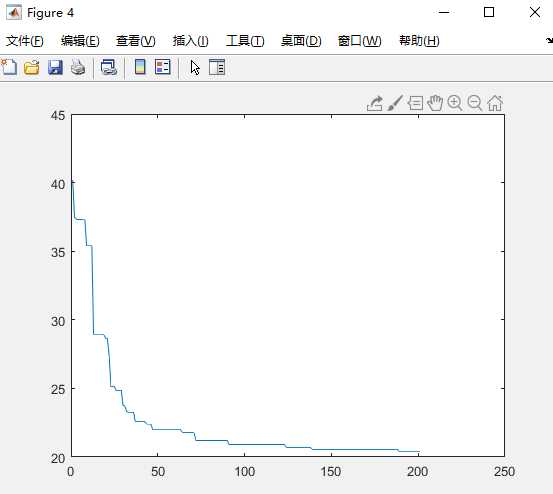
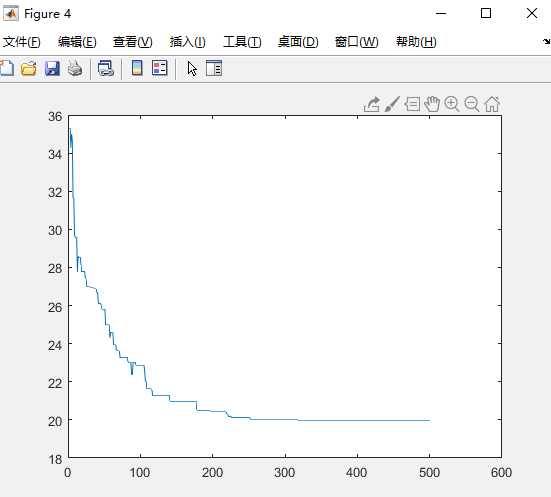
图7 图8


图9 图10
下标是基数的图是迭代200次的,分别是城市的坐标图,初始种群对应各城市之间的连线图,最佳路径图,路径长度图。下标是偶数的是迭代500次的,我定义的城市个数是25个,种群的个数是100个,交查概率为0.8.迭代200次的最佳路径是17 19 1 21 18 4 16 11 8 6 3 5 14 20 2 23 22 24 15 9 10 13 7 25 12 ,路径长度是1.858666e+01,迭代500次的最佳路径是11 6 15 20 8 7 12 5 24 25 22 18 19 23 2 1 21 14 10 13 16 3 17 9 4 ,最短路径是1.733842e+01。有上述可看出,当尘世个数、种群个数、交叉概率相等时,迭代的次数越多,则算出来的路径长度越短,路径也不相同。
图11 图12
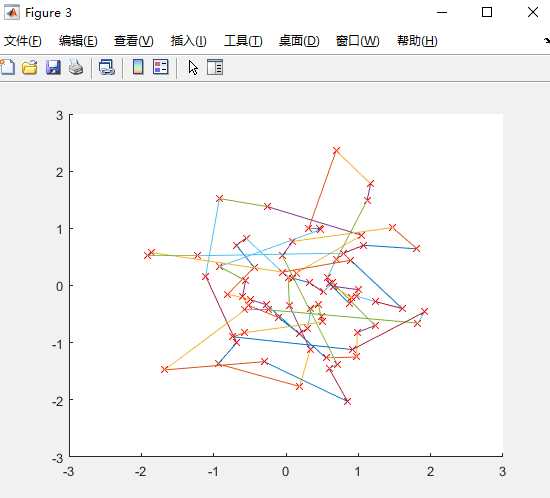
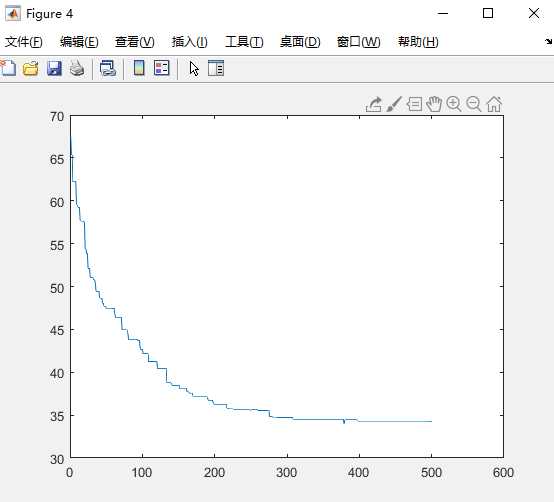
图13 图14
迭代第500次
minlen=3.422104e+01
43 47 33 30 5 49 27 42 9 28 32 16 11 40 31 3 39 20 44 13 4 38 1 14 23 8 29 22 6 10 24 19 18 45 7 15 48 37 12 26 41 17 25 21 2 34 50 46 36 35
对比上面的,改变城市数量,路径变大。
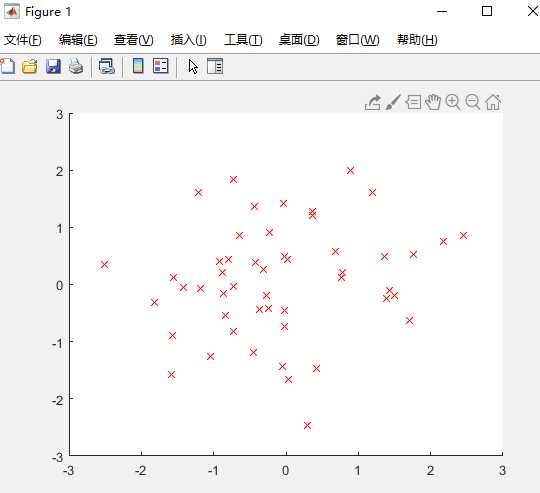
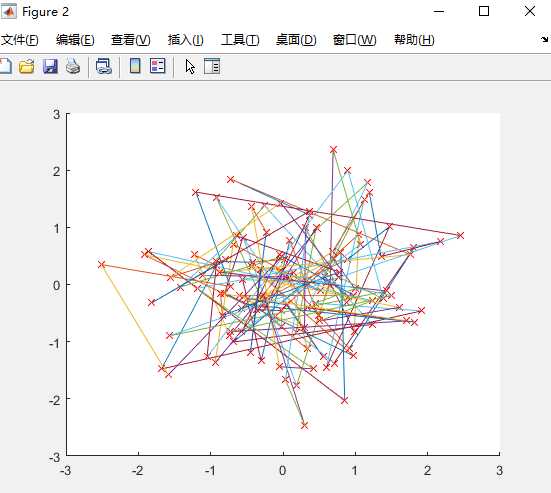
图15 图16
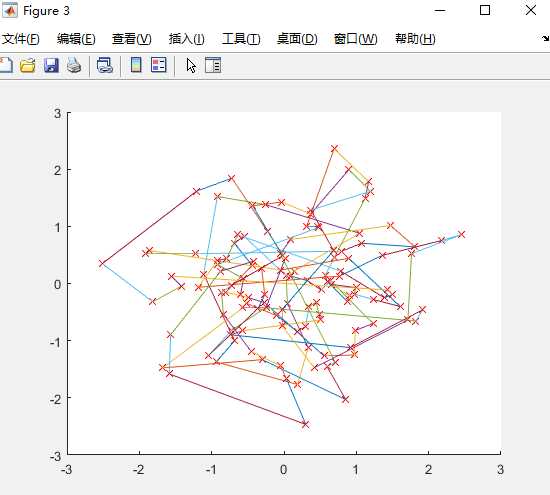
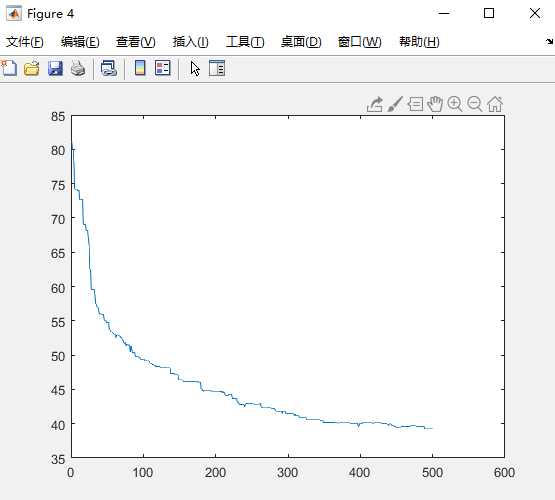
图17 图18
minlen=3.923642e+01
35 10 48 9 20 19 16 23 24 8 7 12 28 30 44 38 13 33 2 1 14 26 47 34 41 18 39 22 3 27 5 40 6 25 45 11 49 15 21 17 32 29 4 37 36 43 50 42 46 31
以上的图,我改变的是变异概率,改为了0.12,原来的是0.05,对比图11 12 13 14发现最小路径变大,最终形成的最短路径图很不清晰,由此看出,变异概率会影响最短路径的长度和最终路径。
我根据以上的实验,改变参数交叉概率,原来是0.8改为了0.5,发现最小路径在变大。由此看出交叉概率会影响最短路径的长度和最终路径。
5、总结
5.1这两个算法的结合提高了算法的时间性能和优化性能,可以快速明显的看出实验的区别。
5.2两个算法结合起来,减少了参数的调整,避免了大量盲目的去迭代次数。
5.3在遗传算法中产生种群,加快了蚂蚁算法的速度避免了求精确解阶段陷入局部最优。
原文:https://www.cnblogs.com/wyf-1999-1--6/p/11891089.html