
Visit node
Traverse(left child)
Traverse(right child)Traverse(left child)
Visit node
Traverse(right child)Traverse(left child)
Traverse(right child)
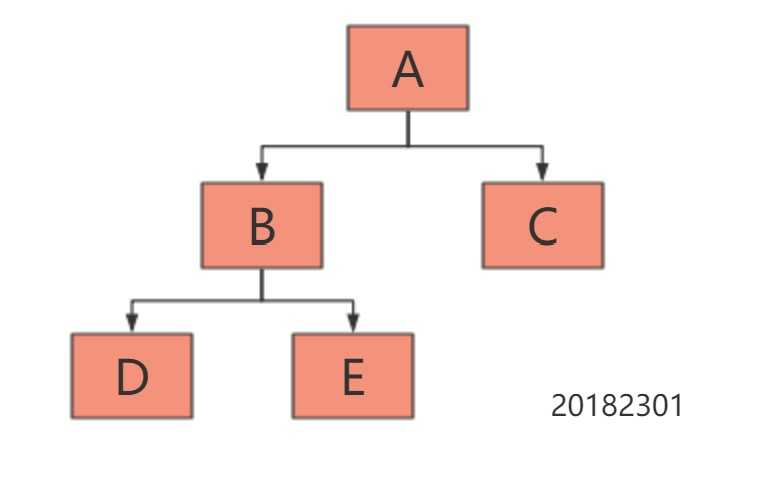
Visit node层序遍历:从根节点开始,访问每一层的所有结点,一次一层。(A->B->C->D->E)
二叉查找树(binary search tree):二叉树定义的扩展,一种带有附加属性的二叉树。附加属性是什么?树中的每个节点,其左孩子都要小于其父节点,而父节点又小于或等于其右孩子。
二叉查找树的类图结构
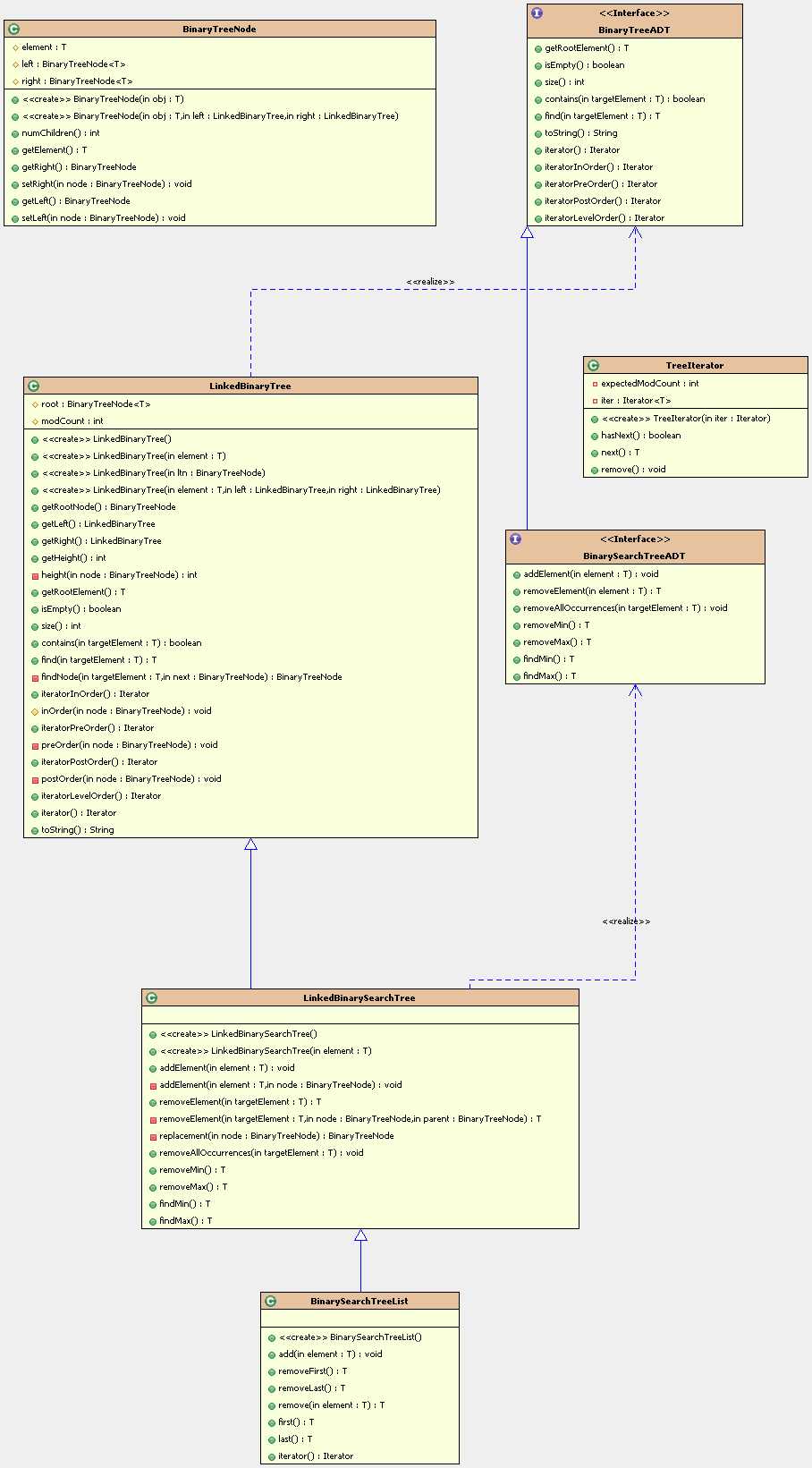
二叉查找树涉及到的基本方法
public void addElement(T element) {
if (!(element instanceof Comparable)) {
throw new NonComparableElementException("LinkedBinarySearchTree");
}
Comparable<T> comElem = (Comparable<T>) element;
if (isEmpty()) {
root = new BinaryTreeNode<T>(element);
} else {
if (comElem.compareTo(root.getElement()) < 0) {
if (root.getLeft() == null) {
this.getRootNode().setLeft(new BinaryTreeNode<T>(element));
} else {
addElement(element, root.getLeft());
}
} else {
if (root.getRight() == null) {
this.getRootNode().setRight(new BinaryTreeNode<T>(element));
} else { addElement(element, root.getRight());
}
}
}
modCount++;
}public T removeElement(T targetElement) {
T result = null;
if (isEmpty()) {
throw new ElementNotFoundException("LinkedbinarySearchTree");
} else {
BinaryTreeNode<T> parent = null;
if (((Comparable<T>) targetElement).equals(root.getElement())) {
result = root.element;
BinaryTreeNode<T> temp = replacement(root);
if (temp == null) {
root = null;
} else {
root.element = temp.element;
root.setLeft(temp.getLeft());
root.setRight(temp.getRight());
}
modCount--;
} else {
parent = root;
if (((Comparable<T>) targetElement)
.compareTo(root.getElement()) < 0) {
result = removeElement(targetElement, root.getLeft(),
parent);
} else {
result = removeElement(targetElement, root.getRight(),
parent);
}
}
}
return result;
}private BinaryTreeNode<T> replacement(BinaryTreeNode<T> node) {
BinaryTreeNode<T> result = null;
if ((node.left == null) && (node.right == null)) {
result = null;
} else if ((node.left != null) && (node.right == null)) {
result = node.left;
} else if ((node.left == null) && (node.right != null)) {
result = node.right;
} else {
BinaryTreeNode<T> current = node.right;// 初始化右侧第一个结点
BinaryTreeNode<T> parent = node;
// 获取右边子树的最左边的结点
while (current.left != null) {
parent = current;
current = current.left;
}
current.left = node.left;
// 如果当前待查询的结点
if (node.right != current) {
parent.left = current.right;// 整体的树结构移动就可以了
current.right = node.right;
}
result = current;
}
return result;
}public void removeAllOccurrences(T targetElement) {
removeElement(targetElement);
try {
while (contains((T) targetElement))
removeElement(targetElement);
}
catch (Exception ElementNotFoundException) {
}
}public T findMin() {
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else {
if (root.left == null) {
result = root.element;
//root = root.right;
} else {
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.left;
while (current.left != null) {
parent = current;
current = current.left;
}
result = current.element;
//parent.left = current.right;
}
//modCount--;
}
return result;
}
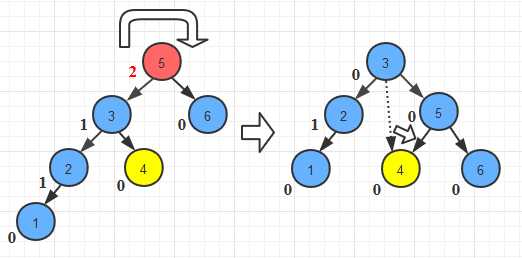
//RR旋转
public AVLTreeNode singleRotateRight(AVLTreeNode w){
AVLTreeNode x= w.getRight();
w.setRight(x.getLeft());
x.setLeft(w);
w.setHeight(Math.max(Height(w.getRight()),Height(w.getLeft()))+1);
x.setHeight(Math.max(Height(x.getRight()),w.getHeight())+1);
return x;
}
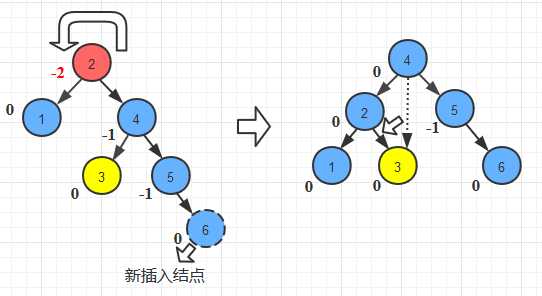
//LL旋转
public AVLTreeNode singleRotateLeft(AVLTreeNode x){
AVLTreeNode w= x.getLeft();
x.setLeft(w.getRight());
w.setRight(x);
x.setHeight(Math.max(Height(x.getLeft()),Height(x.getRight()))+1);
w.setHeight(Math.max(Height(w.getLeft()),x.getHeight())+1);
return w;
}
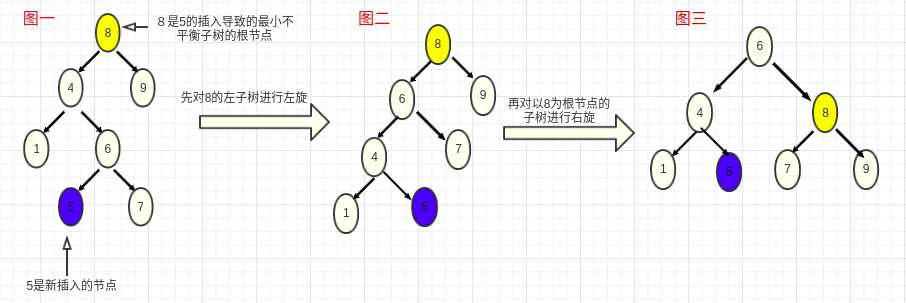
//LR旋转
public AVLTreeNode doubleRotateLeft(AVLTreeNode z){
z.setLeft(singleRotateRight(z.getLeft()));//在X和Y之间旋转
return singleRotateLeft(z);//在Z和Y之间旋转
}
public AVLTreeNode doubleRotateRight(AVLTreeNode x){
x.setRight(singleRotateRight(x.getLeft()));//在Z和Y之间旋转
return singleRotateRight(x);//在X和Y之间旋转}
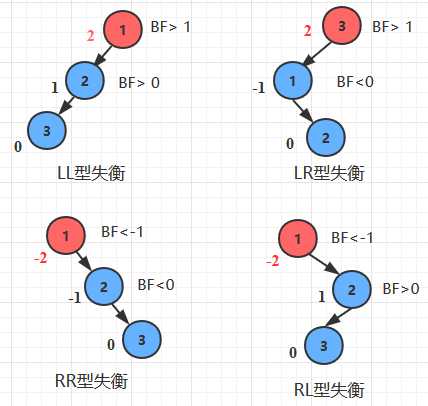
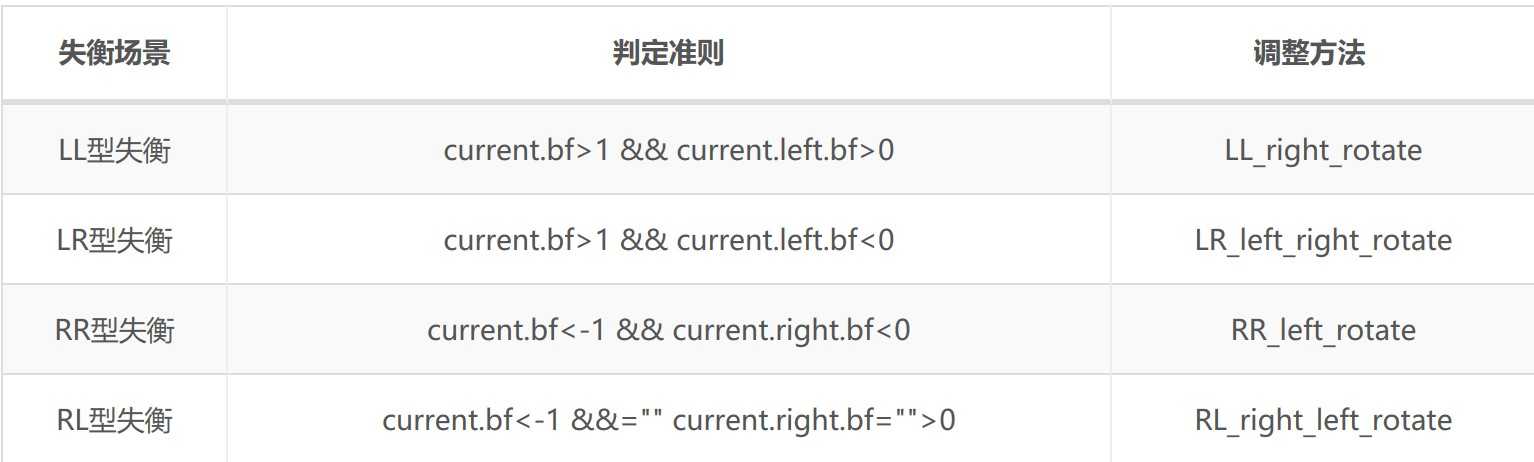
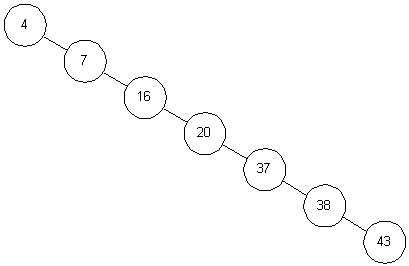
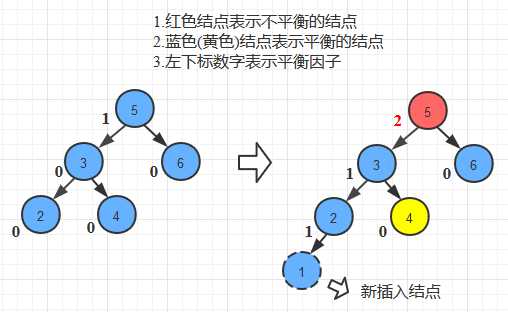
问题2解决方案:(图)
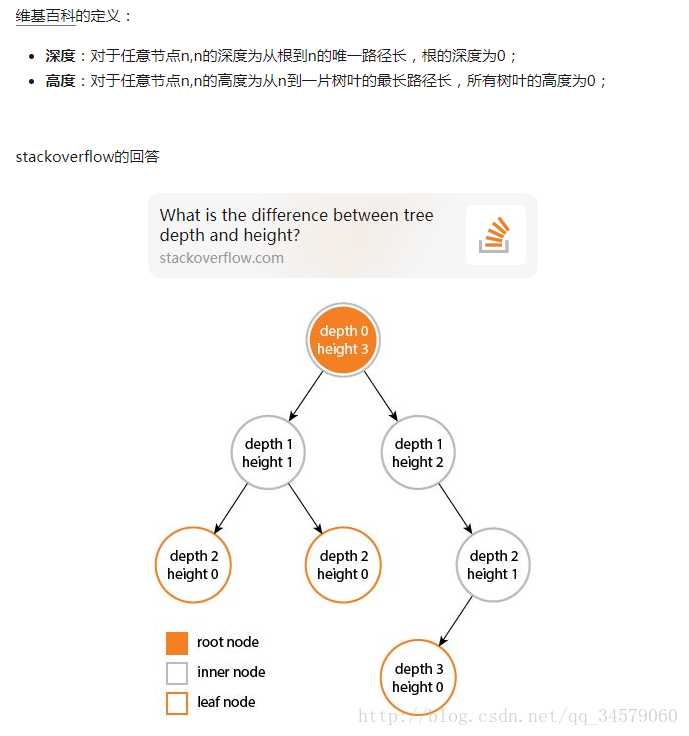
问题3解决方案:(图)
通常使用“熵”来度量样本集合的纯度,“熵”就是物体内部的混乱程度,理论上“熵”的值越小,数据集的“纯度”越高,下面是“熵”的计算公式:

信息增益,指的是测试属性对于样本纯度的增益效果,值越大越好,计算公式为:

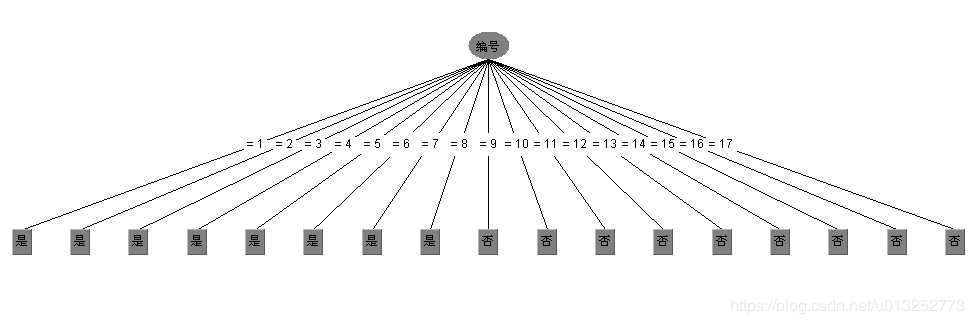
当样本数据中存在ID类型的数据时,由于每条数据的id都不一样,这样id属性对应的熵值是最小的,即纯度是最高的,信息增益是最大的,但是显而易见以id作为根节点是不合适的,这样就会变成一颗只有2层的“宽”树,不具备泛化的能力:

其中:

基尼指数是另一个选择的标准,代表了从样本中任意选择两个样本,类别不一致的概率,所以基尼指数越小,代表样本纯度越高。

属性a的基尼指数定义为属性a各类样本比率的基尼指数和:

左边的对象实例不能是基础数据类型
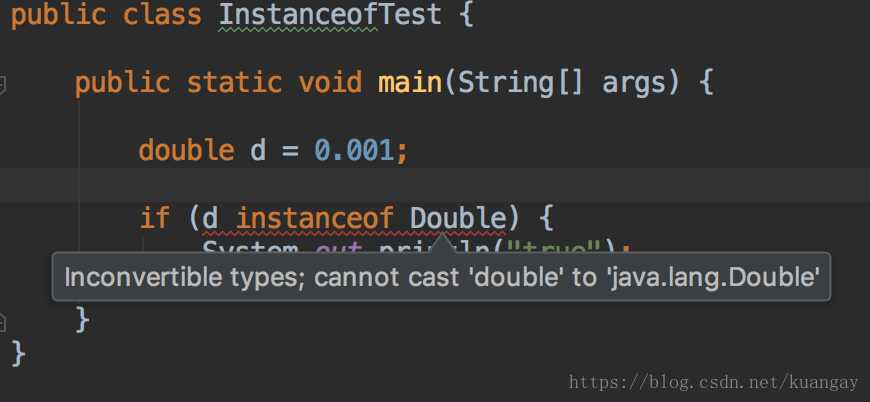
左边的对象实例和右边的类不在同一个继承树上
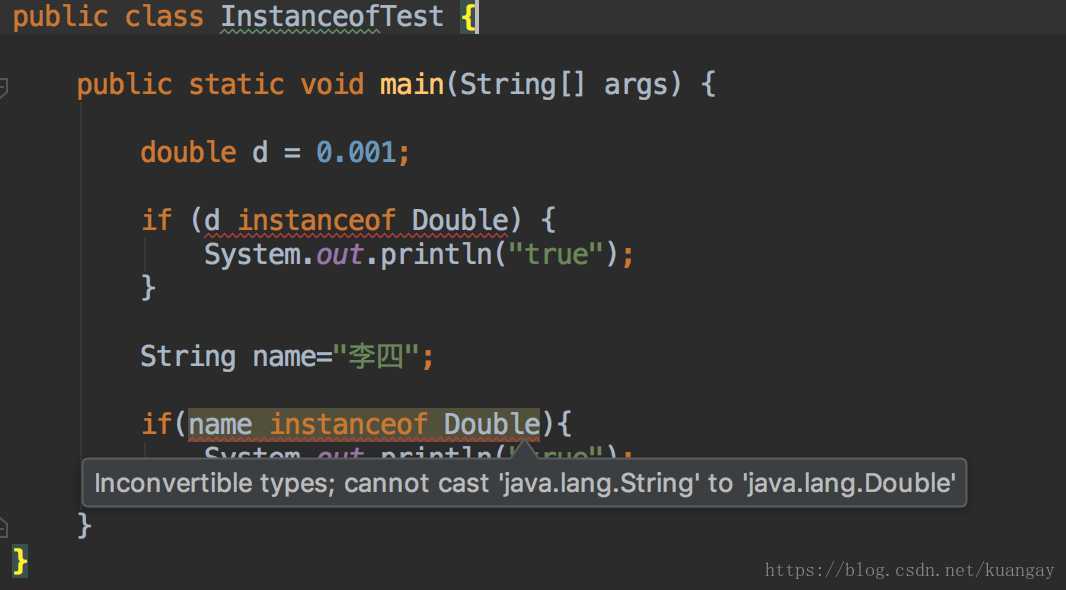

运行结果:
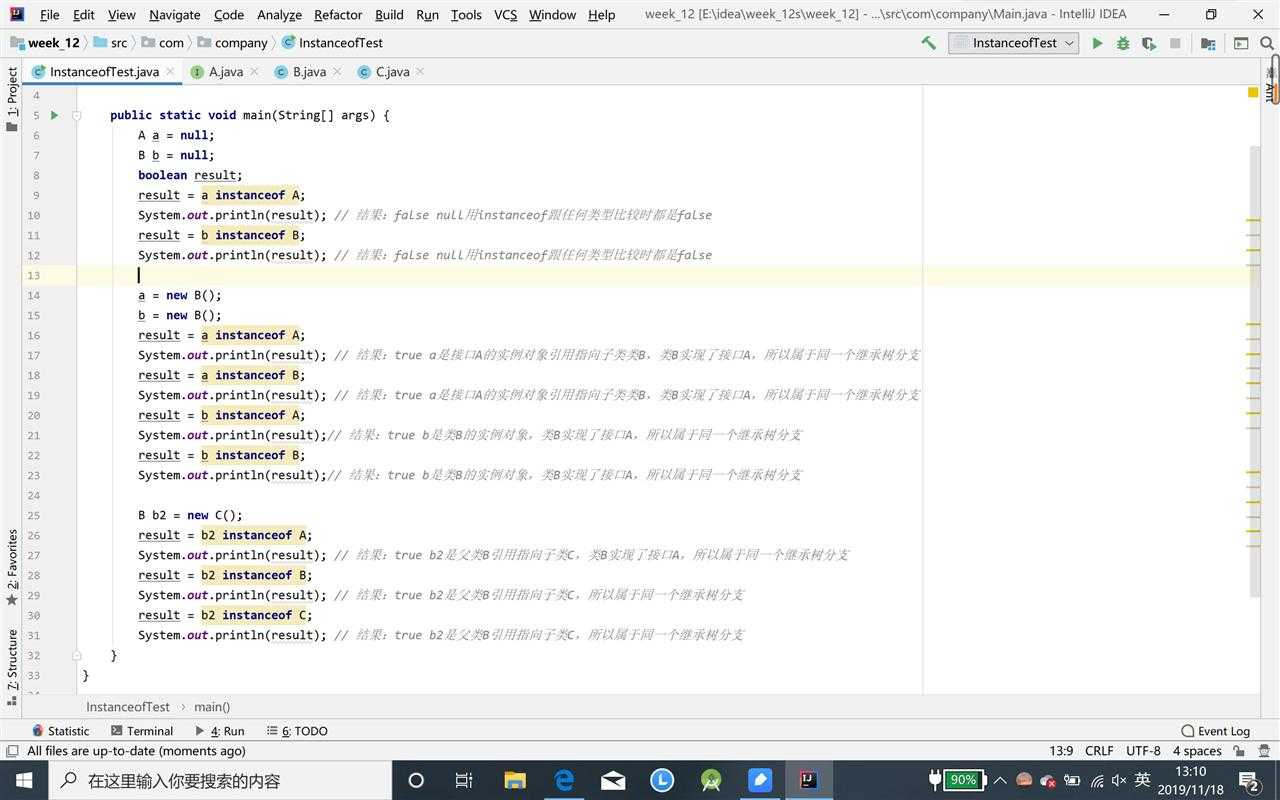

class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class ListNode {
int val;
ListNode next;
ListNode(int val) { this.val = val;}
}
class Solution {
public TreeNode sortedListToBST(ListNode head) {
if(head == null) return null;
return createTree(head, null);
}
public TreeNode createTree(ListNode head, ListNode tail) {
if(head == tail ) return null;
ListNode fast = head;
ListNode slow = head;
while(fast != tail && fast.next != tail) {
fast = fast.next.next;
slow = slow.next;
}
TreeNode node = new TreeNode(slow.val);
node.left = createTree(head, slow);
node.right = createTree(slow.next, tail);
return node;
}
}
public class LED {
public static int[] stringToArrays(String input) {
input = input.trim();
input = input.substring(1, input.length() - 1);
if(input == null) {
return new int[0];
}
String[] patrs = input.split(",");
int[] res = new int[patrs.length];
for(int i = 0; i < res.length; i ++) {
res[i] = Integer.parseInt(patrs[i].trim());
}
return res;
}
public static ListNode stringToListNode(String input) {
int[] nodes = stringToArrays(input);
ListNode dummpy = new ListNode(-1);
ListNode cur = dummpy;
for(int x : nodes) {
cur.next = new ListNode(x);
cur = cur.next;
}
return dummpy.next;
}
public static String treeNodeToString(TreeNode root) {
if(root == null) {
return "[]";
}
String ouput = "";
Queue<TreeNode> nodeQueue = new LinkedList<>();
nodeQueue.add(root);
while(!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.remove();
if(node == null) {
ouput += "null, ";
continue;
}
ouput += String.valueOf(node.val) + ", ";
nodeQueue.add(node.left);
nodeQueue.add(node.right);
}
return "[" + ouput.substring(0, ouput.length() - 2) + "]";
}
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String line = null;
while((line = in.readLine()) != null) {
ListNode head = stringToListNode(line);
TreeNode res = new Solution().sortedListToBST(head);
String result = treeNodeToString(res);
System.out.println(result);
}
}
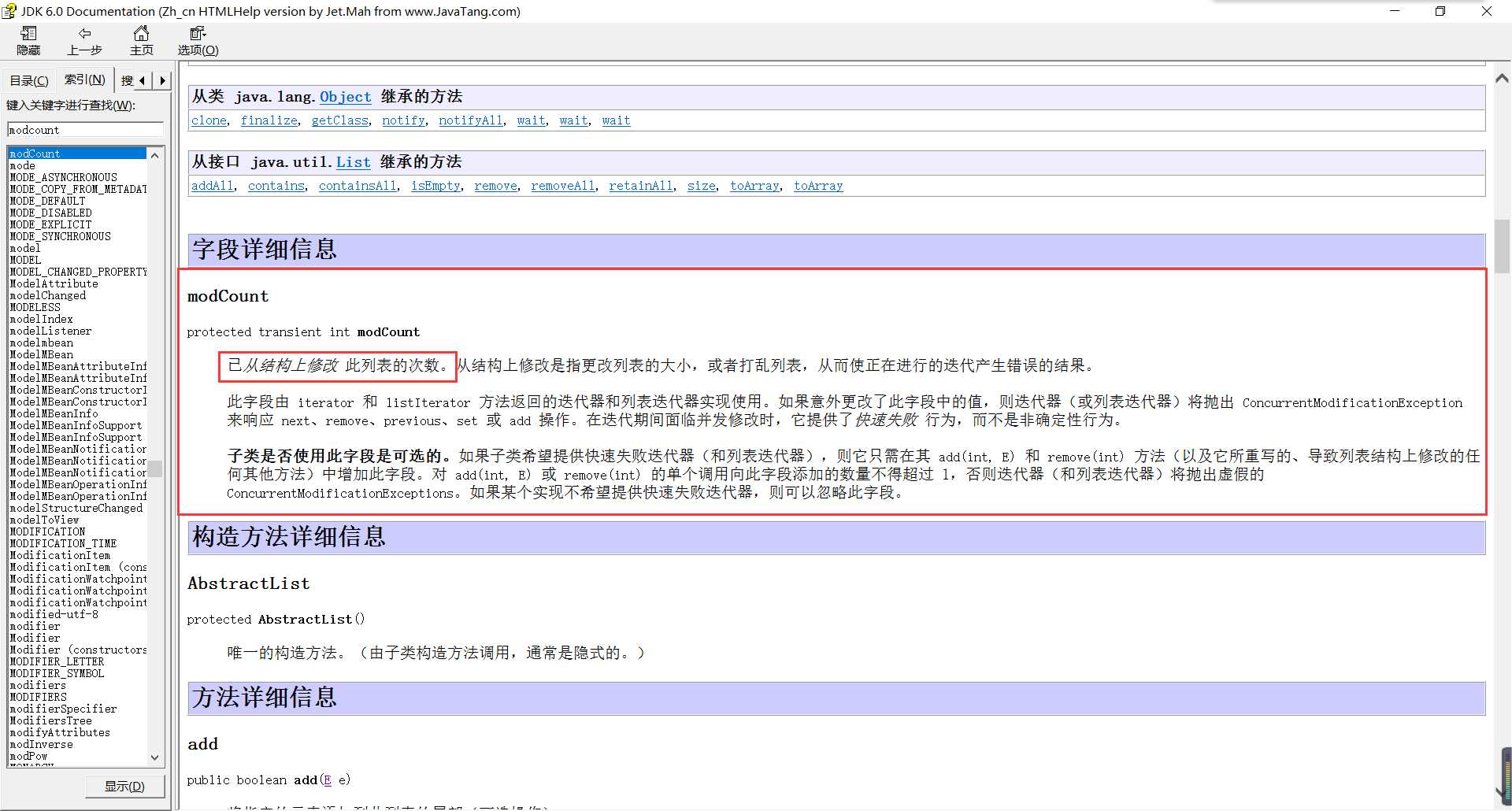
}(statistics.sh脚本的运行结果截图)


- 结对学习内容
- 学习二叉查找树
- 学习树的基本这周有了更多的时间来学习数据结构,感觉有点吃力,要努力!
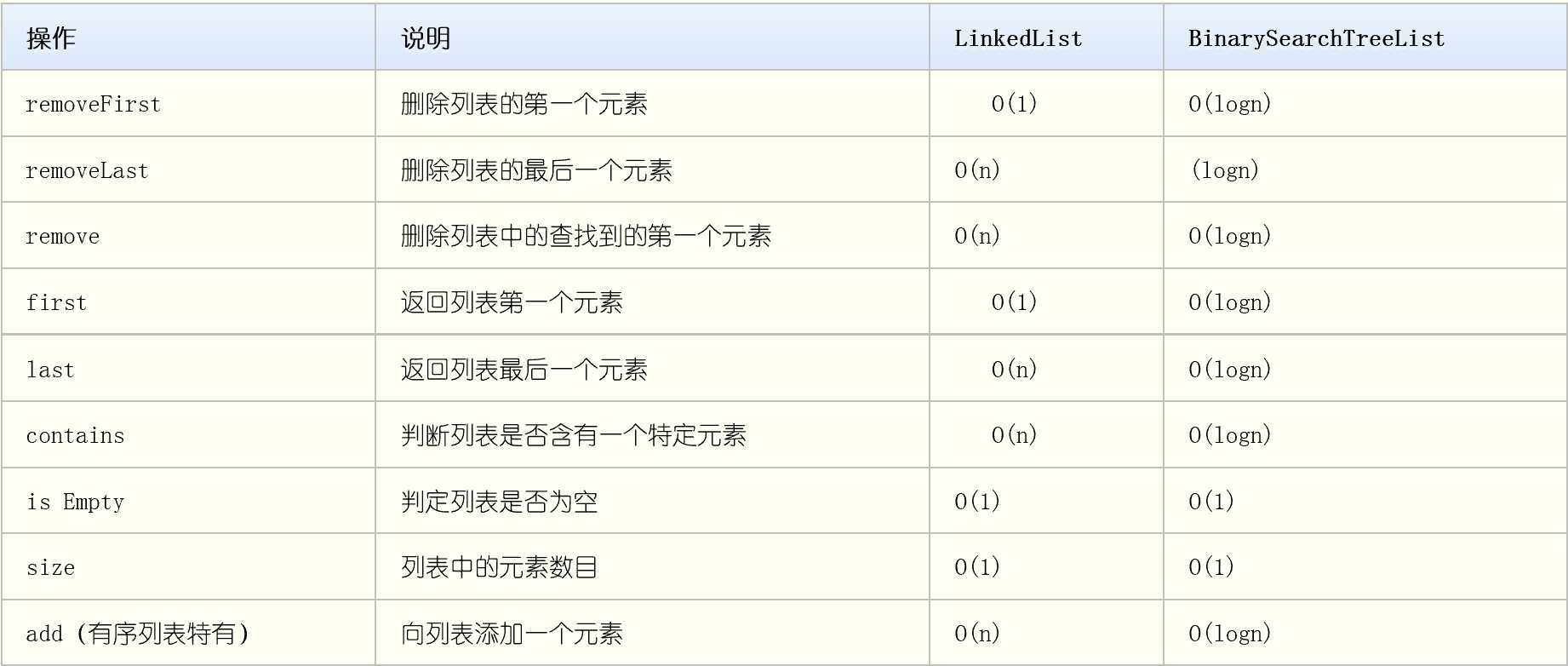
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 69/69 | 2/2 | 30/30 | Scanner |
| 第二、三周 | 529/598 | 3/5 | 25/55 | 部分常用类 |
| 第四周 | 300/1300 | 2/7 | 25/80 | junit测试和编写类 |
| 第五周 | 2665/3563 | 2/9 | 30/110 | 接口与远程 |
| 第六周 | 1108/4671 | 1/10 | 25/135 | 多态与异常 |
| 第七周 | 1946/6617 | 3/13 | 25/160 | 栈、队列 |
| 第八周 | 831/7448 | 1/14 | 25/185 | 查找、排序 |
| 第九周 | 6059/13507 | 3/17 | 35/220 | 二叉查找树 |
尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。
耗时估计的公式:Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。
计划学习时间:30小时
实际学习时间:35小时
改进情况:
这周的别的事情较多,所以很急,以后一定好好把本次课程复习一下。
20182301 2019-2020-1 《数据结构与面向对象程序设计》第9周学习总结
原文:https://www.cnblogs.com/zhaopeining/p/11882950.html