七、排序算法总结五（快速排序）

一、算法思想

　　1、轴点的概念

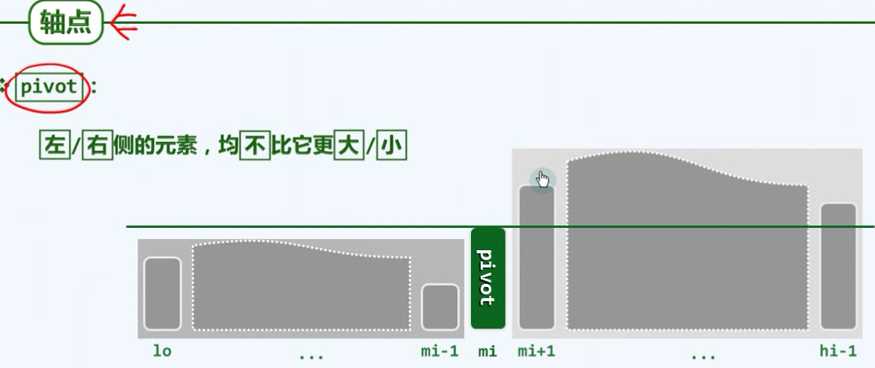
      轴点：左侧的元素均不大于轴点，右侧的元素，均不小于轴点。

　  2、其实这样来说，这个序列已经有了一定的有序性，现在我们已经将整个的数据分为了三个部分：

　　左侧无序部分 + 轴点 +右侧无序部分

　　那么我们接下来要做的，就是将这个过程迭代下去，不断的将无序部分拆分为两个无序部分，直至最后全部有序。

　　这样就会有两个问题：

　　（1）、如何选取一个轴点（有可能我们自己设定的轴点并不存在，所以最好是从数据中选取一个轴点）

　　（2）、如何将这个轴点移动到这样的一个位置：即左侧的数据都比这个轴点小，右侧的数据大于等于这个轴点

二、算法过程

　　算法的具体过程如下：

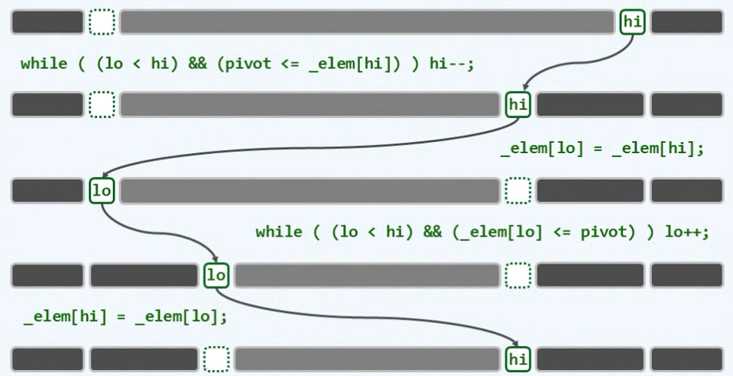
 　　在数据的最开始：灰色部分代表我们将要排序的数据，它的最低位的秩（也就是数组数据的位置）用lo来表示，右侧最高位用hi来表示。

　　 1、随后我们去除左侧的第一个位置的数据当做轴点（也就是  lo位置），可以看到左侧位置是一个虚线框，也就是表示这个位置可以看做是空的。

　　2、我们设立一个哨兵，从最右侧到最左侧一次的遍历每一个位置，如果发现数据比轴点大，那么就接着移动（也就是数据原本就在右侧，所以不用进行操作）

　　如果发现了比轴点小的数据，就移动到左侧那个空节点的位置，这个时候右侧那个数据位置就变成了空。

　　3、随后左侧的哨兵从最左侧到最右侧依次遍历，如果数据都是比轴点小的，那么就不用处理（原本就是在轴点左侧）

　　如果发现了比轴点大的数据，那么就将其移动到 hi哨兵所在的位置。

　　4这样依次循环进行上述的交换，我们可以看到，左侧的数据不断扩大，都比轴点小，右侧数据不断扩展，都比轴点大，中间的无序数据在不断地减少，直到最后只剩下了一个空节点

　　5、将轴点插入到空节点的位置，这样就实现了一次的过程。

　　6、不断迭代进行上述的过程。

三实例

　　有这样的一组数据：

　　在我们遍历的时候,m,每一次的循环遍历过程如下：

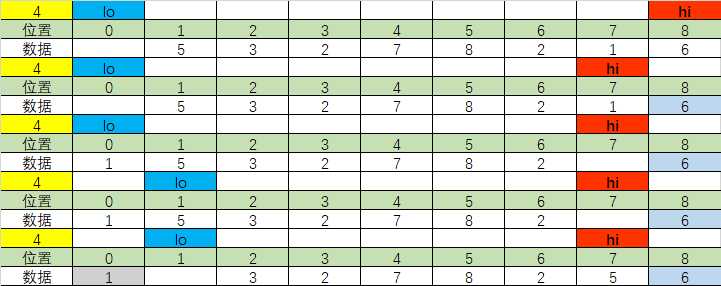
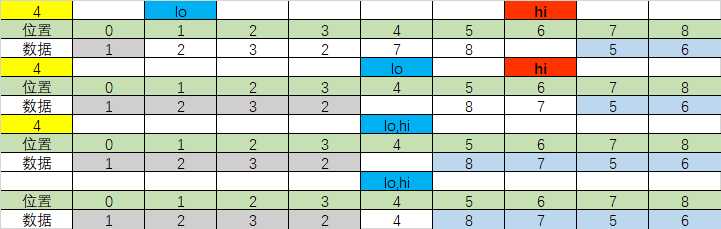
        黄色位置代表当前轴点，黑色位置代表左侧小于轴点区域，蓝色位置代表右侧大于轴点位置，lo代表的是左侧哨兵的当前位置，hi代表的是右侧哨兵的当前位置

　　最后达到的效果就是：

　　在轴点的左侧的数据都是比轴点小，在轴点的右侧的数据都是比轴点大。

　　上面描述的仅仅只是第一个循环的过程，以后的循环都是分为左右两个部分分别按照上面的步骤进行，不断的迭代，使得最后能够达到整体有序的效果。

四、代码实现

#include <iostream>
//#include <stdio.h>
#include <vector>

using namespace std;
int getIndex(vector<int>& nums,int left,int right)   //获取相遇点
{
    int base=nums[left];
    int start=left;    //存储基准数的位置和大小
    while(left<right)  //左右哨兵未相遇
    {
        while(left<right&&nums[right]>=base)right--;  //从右边开始往左寻找小于基准数的数
        nums[left]=nums[right];//右侧小于轴点数据插入左侧空节点
        while(left<right&&nums[left]<=base)left++;   //从左边开始往右寻找大于基准数的数
        nums[right]=nums[left];  //左侧小于轴点数据插入右侧空节点
    }
    //哨兵相遇，则将基准数插入到相遇点来
    nums[left]=base;
    return left; //返回相遇点

}
void QSort(vector<int>& nums,int left,int right)
{
    if(left>=right)return;    
    int index=getIndex(nums,left,right);   //获得相遇点，将原区间分为两个子区间进行递归分治
    QSort(nums,left,index-1);  //左子区间递归
    QSort(nums,index+1,right); //右子区间递归
    return;
}
int main()
{
    cin.clear();
    vector<int>nums;

    int num;
    while(cin>>num)//这里检验输入数据是否符合格式，如果不符合int类型，则退出
    nums.push_back(num);

    int left=0;
    int right=nums.size()-1;

    QSort(nums,left,right);

    for(int i=0;i<=right;i++)cout<<nums[i]<<" ";
    return 0;
}

五、复杂度分析

　　最好情况：最好情况就是我们所说的，轴点正好是我们这个数据的中位数，将左右两个分为规模相等的数据序列，这个时候的复杂度是O(n log n)

　　最坏的情况：非常不均衡，这个时候分为一个n-1的数据序列和一个1的数据序列，这个时候的时间复杂度为：O(n ²)

　　平均的性能：1.39nO(log n)

　　稳定性：不稳定

六、参考内容

　　整体的分析思路参考：《数据结构与算法》邓俊辉2013

　　代码部分参考链接（我自己略有修改）：https://blog.csdn.net/qq_28114615/article/details/86064412

七、改进

　　为了避免出现上述的最坏情况，在选择轴点的时候我们可以通过随机选取或者是一定的选取规则，但是并不能够避免这种最坏情况的发生

七、排序算法总结五（快速排序）

原文：https://www.cnblogs.com/fantianliang/p/11896239.html