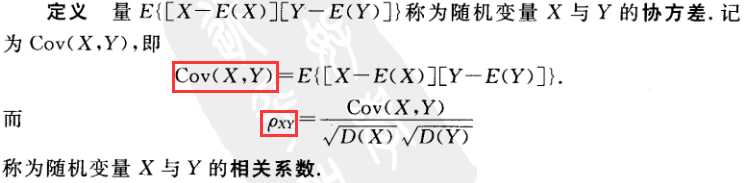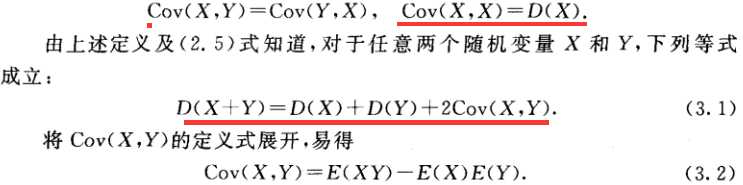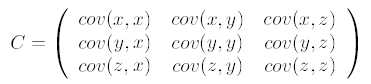均值:描述的是样本集合的中间点。

方差:描述的是样本集合的各个样本点到均值的距离之平均,一般是用来描述一维数据的。

协方差:
- 是一种用来度量两个随机变量关系的统计量。
- 只能处理二维问题。
- 计算协方差需要计算均值。
如下式:
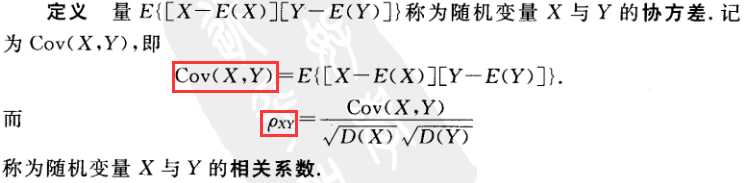
方差与协方差的关系
方差是用来度量单个变量 “ 自身变异”大小的总体参数,方差越大表明该变量的变异越大
协方差是用来度量两个变量之间 “协同变异”大小的总体参数,即二个变量相互影响大小的参数,协方差的绝对值越大,则二个变量相互影响越大。
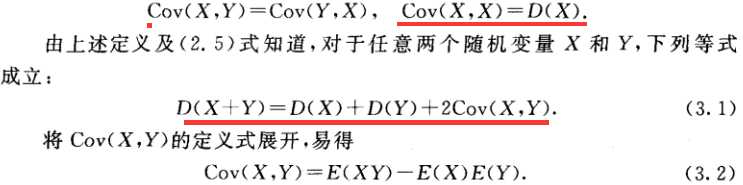
协方差矩阵:
- 协方差矩阵能处理多维问题;
- 协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。
- 协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。
- 样本矩阵中若每行是一个样本,则每列为一个维度,所以计算协方差时要按列计算均值。
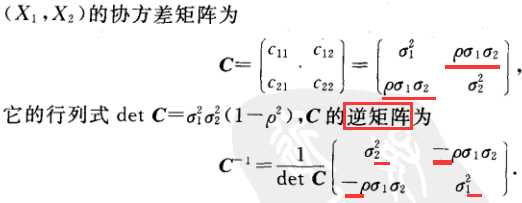
如果数据是3维,那么协方差矩阵是:
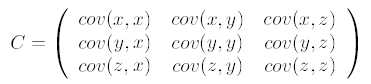
特征值与特征向量




线性变化:
线性变换(线性映射)是在作用于两个向量空间之间的函数,它保持向量加法和标量乘法的运算,从一个向量空间变化到另一个向量空间。实际上线性变换表现出来的就是一个矩阵。
特征值和特征向量是一体的概念:
对于一个给定的线性变换(矩阵A),它的特征向量 ξ 经过这个线性变换之后,得到的新向量仍然与原来的ξ保持在同一條直線上,但其长度也许會改变。一个特征向量的长度在该线性变换下缩放的比例(λ)称为其特征值(本征值)。
数学描述:Aξ=λξ
在线性变换A的作用下,向量ξ仅仅在尺度上变为原来的λ倍。称ξ是线性变换A的一个特征向量,λ是对应的特征值。
- 矩阵是一个表示二维空间的数组,矩阵可以看做是一个变换。在线性代数中,矩阵可以把一个向量变换到另一个位置,或者说从一个坐标系变换到另一个坐标系。矩阵的“基”,实际就是变换时所用的坐标系。
- 矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
- 任意给定一个矩阵A,并不是对所有的向量x它都能拉长(缩短)。凡是能被矩阵A拉长(缩短)的向量就称为矩阵A的特征向量(Eigenvector);拉长(缩短)的量就是这个特征向量对应的特征值(Eigenvalue)。
- 一个矩阵可能可以拉长(缩短)多个向量,因此它就可能有多个特征值。
- 对于实对称矩阵来说,不同特征值对应的特征向量必定正交。
- 一个变换矩阵的所有特征向量组成了这个变换矩阵的一组基。所谓基,可以理解为坐标系的轴。我们平常用到的大多是直角坐标系,在线性代数中可以把这个坐标系扭曲、拉伸、旋转,称为基变换。我们可以按需求去设定基,但是基的轴之间必须是线性无关的,也就是保证坐标系的不同轴不要指向同一个方向或可以被别的轴组合而成,否则的话原来的空间就“撑”不起来了。在主成分分析(PCA)中,我们通过在拉伸最大的方向设置基,忽略一些小的量,可以极大的压缩数据而减小失真。
- 变换矩阵的所有特征向量作为空间的基之所以重要,是因为在这些方向上变换矩阵可以拉伸向量而不必扭曲它,使得计算大为简单。因此特征值固然重要,但我们的终极目标却是特征向量。
- 同一特征值的任意多个特征向量的线性组合仍然是A属于同一特征值的特征向量。
顾名思义,特征值和特征向量表达了一个线性变换的特征。在物理意义上,一个高维空间的线性变换可以想象是在对一个向量在各个方向上进行了不同程度的变换,而特征向量之间是线性无关的,它们对应了最主要的变换方向,同时特征值表达了相应的变换程度。
具体的说,求特征向量,就是把矩阵A所代表的空间进行正交分解,使得A的向量集合可以表示为每个向量a在各个特征向量上的投影长度。我们通常求特征值和特征向量即为求出这个矩阵能使哪些向量只发生拉伸,而方向不发生变化,观察其发生拉伸的程度。这样做的意义在于,看清一个矩阵在哪些方面能产生最大的分散度(scatter),减少重叠,意味着更多的信息被保留下来。
Referee:
特征值和特征向量的几何和物理意义
来源:https://www.cnblogs.com/fuleying/p/4462850.html
均值、方差、协方差、协方差矩阵、特征值、特征向量
原文:https://www.cnblogs.com/rgxx/p/11938647.html