树的定义是,除根结点之外,树的每个结点都恰好有一个父结点。
而如果违背了这一个前提,即允许树的每个结点连通多个其它结点,不再有父亲、孩子之说,即得到孩子的概念
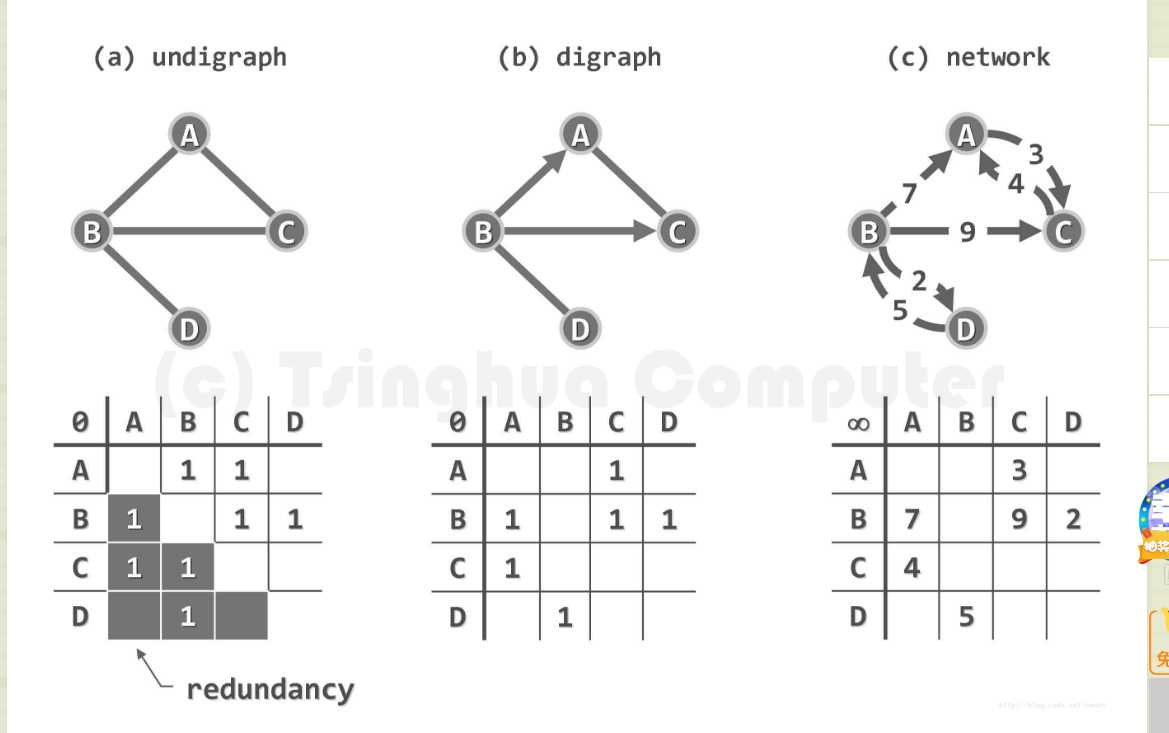
一、无向图
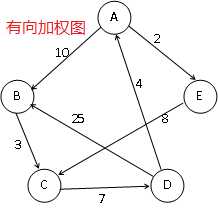
二、有向图
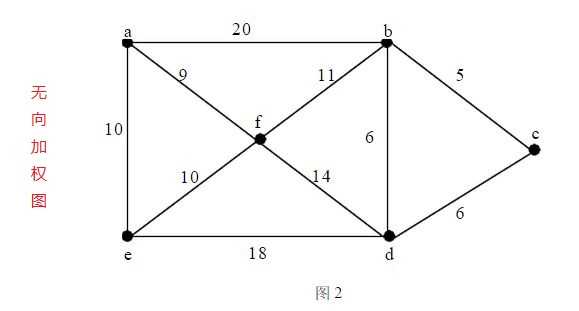
三、网络(加权图)
四、常用的图算法
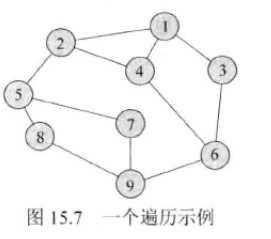
-无向连通图 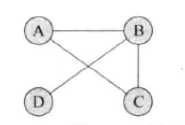
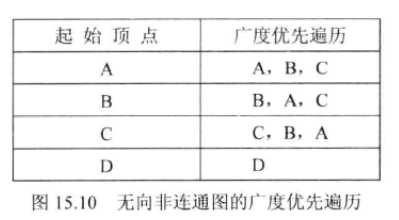
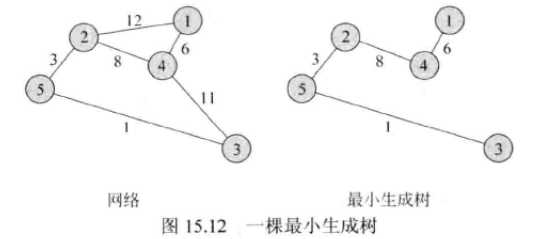
五、图的实现策略
double i = Double.POSITIVE_INFINITY; // i表示为无限大
public static final double POSITIVE_INFINITY = 1.0 / 0.0;问题2:书上说测试连通性,通过比较广度优先遍历中的顶点数目和图中的顶点数目是否相等来判断。也就是说任意一个顶点都必须满足这个条件。那么,我们为什么不只要判断出有广度优先遍历的顶点数目和图中的顶点数目不相等的时候就不连通呢,这样可以有效减少遍历次数,优化算法的效率。
问题3解决方案:其实这个问题非常简单,只是自己的脑子没扭过来,直接把那个1变为需要加上的权重就实现了加权图。
Graph类补全时遇到一些困难。isEmpty方法,原本的代码如下:public boolean isEmpty()
{
if (numVertices == 0)
{
return true;
}
else {
return false;
}
}public boolean isEmpty()
{
return (numVertices == 0)
}自己想了想发现这样的确会简单很多。这告诉我们应该多多想想算法的优化。
private Iterator<T> iteratorBFS(int startIndex) {
Integer x;
QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();
UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();
//索引无效,返回空
if (!indexIsValid(startIndex))
return resultList.iterator();
boolean[] visited = new boolean[maxCount];
//把所有顶点设为false,白色
for (int i = 0; i < maxCount; i++)
visited[i] = false;
//进入队列的为true,即访问过的,灰色
traversalQueue.enqueue(startIndex);
visited[startIndex] = true;
while (!traversalQueue.isEmpty()) {
//出队列涂黑存入resultList中
x = traversalQueue.dequeue();
resultList.addToRear((T) nodelist.get(x).getElement());
//如果进入resultList的顶点还有相邻的未访问过的顶点,将其涂灰入队
for (int i = 0; i < maxCount; i++) {
if (hasEdge(x, i) && !visited[i]) {
traversalQueue.enqueue(i);
visited[i] = true;
Int++;
}
}
}
return new GraphIterator(resultList.iterator());
}
教材学习中的问题和解决过程, 一个问题加1分
代码调试中的问题和解决过程, 一个问题加1分
代码中值得学习的或问题:
进度条有记录+1.
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 59/200 | 2/2 | 20/20 | |
| 第三周 | 292/331 | 2/4 | 20/40 | |
| 第四周 | 677/969 | 2/6 | 20/60 | |
| 第五周 | 661/1265 | 2/8 | 20/80 | |
| 第六周 | 1299 /2554 | 2/10 | 20/100 | |
| 第七周 | 1500/4054 | 2/12 | 20/120 | |
| 第九周 | 6049/10103 | 2/14 | 20/140 | |
| 第十周 | 1049/11152 | 2/16 | 20/160 |
计划学习时间:20小时
实际学习时间:20小时
改进情况:越到后面,学习越紧张,顶住!!!
20182322 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结
原文:https://www.cnblogs.com/wmh20182322/p/11945469.html