主席树学习笔记

参考博文

• https://blog.csdn.net/bestFy/article/details/78650360

前置知识

• 权值线段树
• 权值线段树和普通线段树区别在于他们维护的东西不一样：
  • 权值线段树维护值域，普通线段树维护区间。

初始主席树

• 主席树的发明人的名字简称是\(hjt\)，所以得名主席树。
• 主席树全称是可持久化权值线段树。
• 可持久化思想可以观察此图来理解：

• 

• 图中红色的为历史节点，蓝色的是新建节点(修改后的节点)。
• 每次只更改一条链，也就是\(logn\)个点。

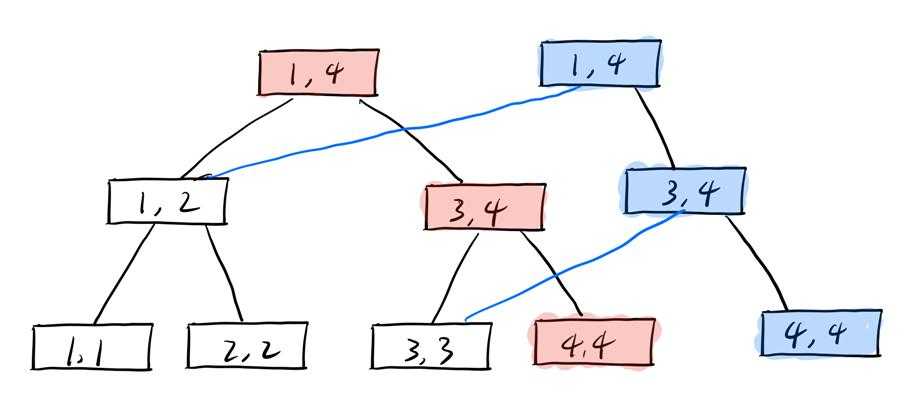
• 主席树不采用\(p*2,p*2+1\)的方式来表示左右儿子，而是需要动态开点地保存左右儿子的编号，从而节约空间。

经典入门问题

• 洛谷3834：主席树模板
• 给定一个序列长度为\(n\)，给定\(m\)个询问，每次询问指定的闭区间\([L,R]\)内查找区间内第\(k\)小值。
• 数据范围\(1\leq n,m\leq 2*10^5,-10^9\leq a_i\leq 10^9\)。

问题分析

• 首先考虑从区间\([1,n]\)查询区间第\(k\)小要怎么做，这里很明显，可以使用权值线段树来做。
• 这里给一道例题在这。链接。
• 那接下来考虑这个问题，先简化一下问题，求区间\([1,R]\)第\(k\)小的数字要怎么做？
• 首先找到插入\(R\)节点时的历史版本，然后用普通权值线段树就可以了。
• 那么现在拓展到原问题，求\([L,R]\)区间的第\(k\)小值。
• 这里需要运用前缀和的知识。对于求\([L,R]\)的值，我们只需要用\([1,R]\)的信息减去\([1,L-1]\)的信息。
• 模拟一下这个过程：
• 假设序列长度为\(4\)，序列为\(3\ 1\ 2\ 4\)，查询\([2,3]\)区间第\(2\)小的数字。
• 插入\(3\)

• 

• 插入\(1\)

• 

• 插入\(2\)

• 

• 插入\(4\)

• 

• 序列为\(3\ 1\ 2\ 4\)。
• 我们现在要查询\([2,3]\)区间内第\(2\)小的数字，首先需要把第\(1\)棵线段树和第\(3\)棵线段树拿出来

• 

• 我们发现对应节点相减，刚刚好是\([2,3]\)区间内某个范围数的个数，比如说\([1,2]\)这个节点相减为\(2\)，说明在原序列\([2,3]\)这个区间内有两个数在\([1,2]\)范围内。\([3,4]\)相减为\(0\)，说明原序列\([2,3]\)区间中没有数字在\([3,4]\)范围内。

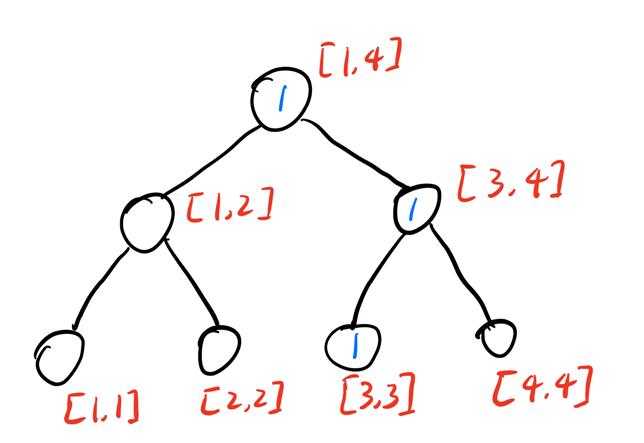
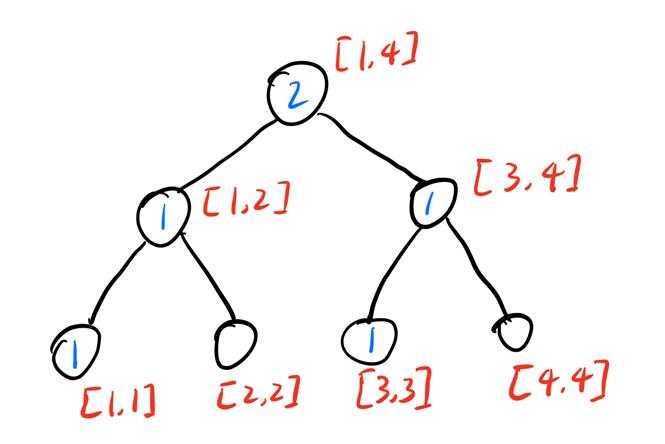
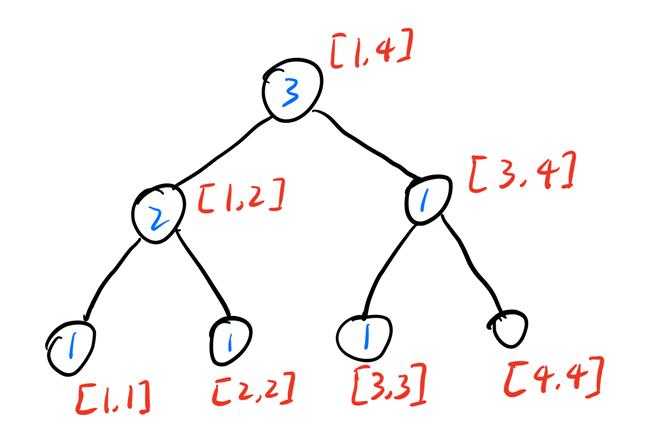
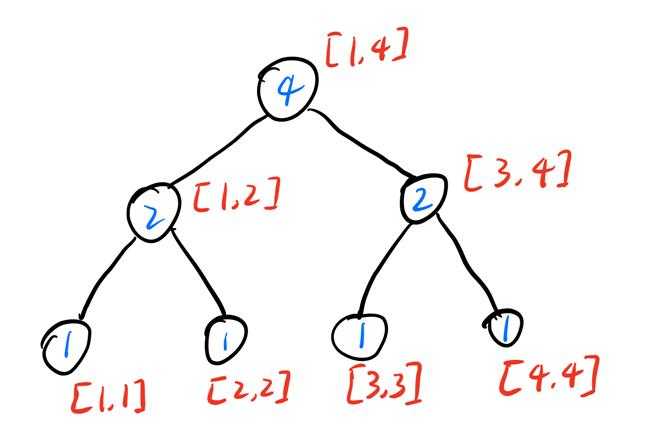
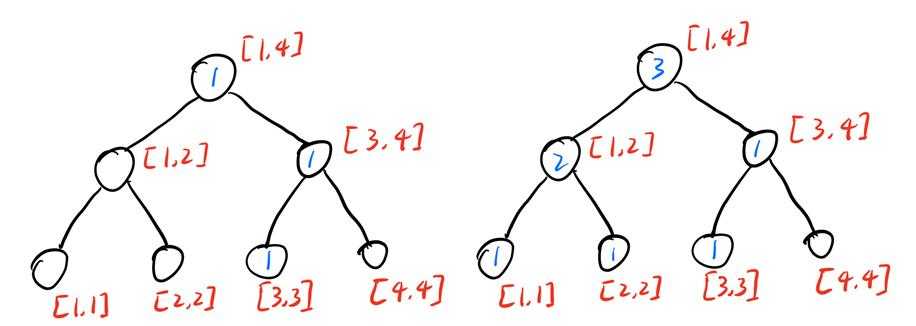
• 那我们从根节点开始，计算左孩子范围的数字\(num\)，如果\(k\leq num\)，说明第\(k\)小的数字在左子树中，递归进入左子树，否则进入右子树。

• 空间分析：

  • 因为我们是动态开点，首先最初的线段树有\(2n-1\)个节点，每次操作会增加\(logn\)个节点。最坏情况下总结点数\(2n-1+nlogn\)，那么对于\(10^5\)来讲，开\(20*10^5\)较为妥当，但这时候还是不要吝惜空间比较好，所以直接用\(2^5*10^5\)开空间。

• 至此，问题解决，详见代码。

#include<bits/stdc++.h>
using namespace std;

const int maxn = 2e5 + 10;
int a[maxn], num[maxn], n, m, len;

int sum[maxn<<5]; //sum(i)存储根为i的子树的大小
int ls[maxn<<5];  //左儿子
int rs[maxn<<5];  //右儿子
int rt[maxn<<5];  //根节点
int tot;          //一共出现多少个根

int build(int l, int r)
{
    int root = ++tot;
    if(l == r) return root;
    int mid = (l + r) >> 1;
    ls[root] = build(l, mid);
    rs[root] = build(mid+1, r);
    return root;   //返回这课子树的根节点
}

//插入操作
int update(int pre, int l, int r, int k)
{
    int root = ++tot;
    ls[root] = ls[pre], rs[root] = rs[pre], sum[root] = sum[pre] + 1;
    if(l == r) return root;
    int mid = (l + r) >> 1;
    //更改左子树或右子树
    if(k <= mid) ls[root] = update(ls[pre], l, mid, k);
    else rs[root] = update(rs[pre], mid+1, r, k);
    return root;
}

//查询操作
int query(int u, int v, int l, int r, int k)
{
    if(l == r) return l;
    int x = sum[ls[v]] - sum[ls[u]];
    int mid = (l + r) >> 1;
    if(k <= x) return query(ls[u], ls[v], l, mid, k);
    else return query(rs[u], rs[v], mid+1, r, k - x);
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        num[i] = a[i];
    }

    //离散化
    sort(num+1, num+1+n);
    len = unique(num+1, num+1+n) - num - 1;

    rt[0] = build(1, len);
    for(int i = 1; i <= n; i++)
    {
        int t = lower_bound(num+1, num+1+len, a[i]) - num;
        rt[i] = update(rt[i-1], 1, len, t);
    }
    int l, r, k;
    while(m--)
    {
        scanf("%d%d%d", &l, &r, &k);
        int ans = query(rt[l-1], rt[r], 1, len, k);
        printf("%d\n", num[ans]);
    }

    return 0;
}

主席树学习笔记

原文：https://www.cnblogs.com/zxytxdy/p/11956952.html