题目链接:http://poj.org/problem?id=2411
给你一个 \(n \times m (1 \le n,m \le 11)\) 的矩阵,你需要用若干 \(1 \times 2\) 的砖块铺满这个矩阵。
要求不能有砖块重叠,并且矩阵中的每个各自都需要铺满。
比如下图中描述的就是一个 \(10 \times 11\) 的矩阵的一种合法的铺法。

问满足要求的 方案数 。
比如下图中的左边5幅图片对应的是 \(2 \times 4\) 的矩阵的所有合法方案;右边的3幅图片对应的是 \(2 \times 3\) 的矩阵的所有合法方案。

轮廓线DP 的思想建立在如下一种思维模式下:
我按行号从小到大放,相同行的情况下我按照列号从小到大放。
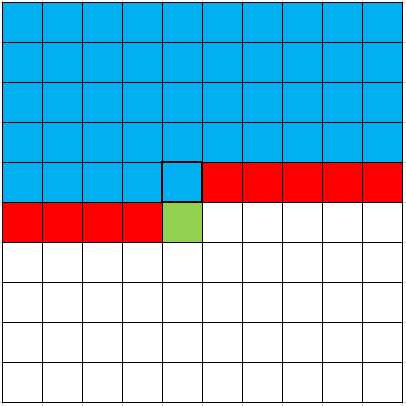
那么在某一个时刻我总能达到这样一个场景,如下图:
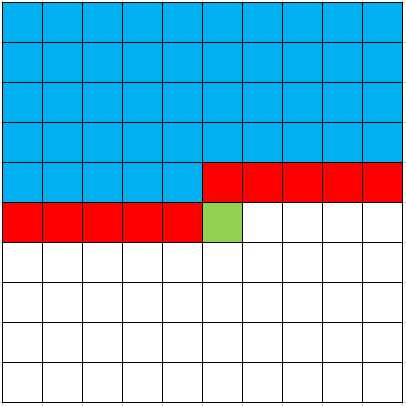
在同种我们用3种颜色描绘了三种不同状态的点:
解释:
我这里称呼的“确定点”指的是已经放好砖块的点;
“不确定点”指的是不确定有没有放的点(可能放了也可能没放)。
我们用数字 1 表示放了;用数字 0 表示没放。
我们假设左上角坐标是 \((1,1)\) (实际实现的时候其实坐标不一定,具体看代码对应的左上角坐标),并且设我们当前正在遍历的点是 \((i,j)\) ,那么:
如果 \(j=1\) ,则说明
在处理 \((i,j)\) 之前, \((1,1)\) 到 \((i-2,m)\) 都是确定点,如图:
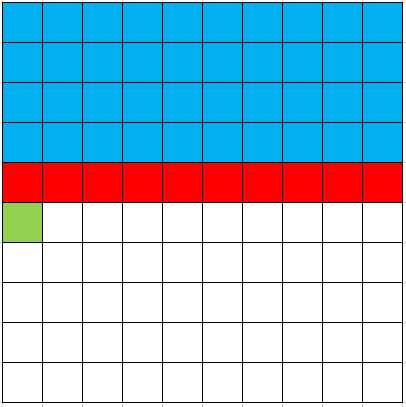
在处理 \((i,j)\) 之后, \((1,1)\) 到 \((i-1,1)\) 都是确定点,如图:
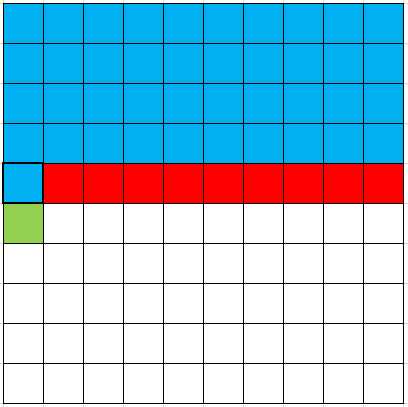
如果 \(j \gt 1\) ,则说明
在处理 \((i,j)\) 之前, \((1,1)\) 到 \((i-1,j-1)\) 都是确定点,如图:
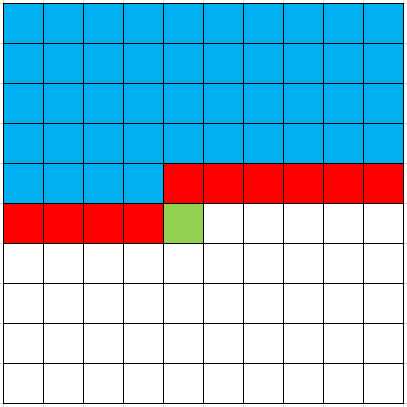
在处理 \((i,j)\) 之后, \((1,1)\) 到 \((i-1,j)\) 都说是确定点,如图:
所以我们可以用状态 \(f_{i,j,k}\) (其中 \(1 \le i \le n, 1 \le j \le m, 0 \le k \le 2^m\) )来表示当前我们遍历到 \((i,j)\) 时,以 \((i,j)\) 结尾的 \(m\) 个元素的状态为 \(k\) 时的方案总数( \(k\) 的二进制表示的第0位对应 \((i,j)\) 目前有无放置,第1位对应 \((i,j)\) 的前一个格子目前有无放置,……)
那么如何放置呢?我们可以粗略地分为如下四种情况:
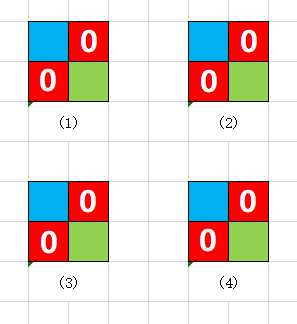
然后我们可以顺着推到状态转移方程。
初始状态是 \(f(0,m,不确定区域全为1)=1\) ,这个状态其实是表示第 \(0\) 行全都填满(因为第 \(0\) 行不可能被填所以就干脆设该状态为不确定区域全为1)对应的方案数为 \(1\) 。
另一方面需要注意:注意每一排第一个是没有办法横着摆的!
最后输出 \(f(n,m,不确定区域全部为1)\) 即可。
实现代码如下:
#include <cstdio>
#include <cstring>
int n, m;
long long f[13][13][1<<13];
int main() {
while (~scanf("%d%d", &n, &m) && n) {
memset(f, 0, sizeof(f));
f[0][m-1][(1<<m)-1] = 1;
for (int r = 1; r <= n; r ++) { // 枚举当前行号r
for (int c = 0; c < m; c ++) { // 枚举当前列号c
int pr, pc; // pr,pc分别表示上一个状态的行号和列号
if (!c) pr = r-1, pc = m-1;
else pr = r, pc = c-1;
for (int k = 0; k < (1<<m); k ++) { // k表示上一个状态
/**
情况1:当前位置不放置木板,这种情况下要求 上一个状态的首个不确定格子是放置了木板的,
即: k & (1 << (m-1)) != 0
*/
if (k & (1 << (m-1))) { // 说明上一个状态的最前面的格子已填充
int s = (k << 1) ^ (1 << m); // s表示当前状态
f[r][c][s] += f[pr][pc][k];
}
/**
情况2:当前位置放置一块竖着放的木板,这种情况下要求
上一个状态的首个不确定格子是没有放置模板的,
即: k & (1 << (m-1)) == 0
*/
if (r > 1 && (k & (1 << (m-1))) == 0) { // 说明上一个状态的最前面的格子(即当前状态的上面的那个格子)未填充
int s = (k << 1) ^ 1; // s表示当前状态
f[r][c][s] += f[pr][pc][k];
}
/**
情况3:当前位置放置一块横着放的木板,这种情况下要求
上一个状态的最后一个不确定格子是没有放置模板的,
并且要求上一个状态的最前面一个不确定格子是必须放置模板的(此时不放,没有别的时间放!),
即: k & 1 == 0
*/
if (c > 0 && (k & 1) == 0 // 说明上一个状态的最后面的格子(即当前状态的左边的那个格子)未填充
&& (k & (1 << (m-1))) ) { // 说明上一个状态的最前面的格子已填充
int s = (k << 1) ^ 3 ^ (1 << m); // s表示当前状态
f[r][c][s] += f[pr][pc][k];
}
}
}
}
printf("%lld\n", f[n][m-1][(1<<m)-1]);
}
return 0;
}在实现的过程中,因为我们发现:当前的这个状态 \(f_{i,j,s}\) 和它的上一步状态 \(f_{i',j',s'}\) 是有着位置上的衔接关系的,所以我们可以开一个滚动数组来表示位置。
具体地,将 \(f_{i,j,s}\) 用 \(f_{now,s}\) 来表示,而将 \(f_{i',j',s'}\) 用 \(f_{now^1, s'}\) 来表示。
实现代码如下(注意这里行号和列号都从0开始了):
#include <cstdio>
#include <cstring>
int n, m;
long long f[2][1<<13];
int main() {
while (~scanf("%d%d", &n, &m) && n) {
memset(f[0], 0, sizeof(f[0]));
int now = 0;
f[now][(1<<m)-1] = 1;
for (int r = 0; r < n; r ++) { // 枚举当前行号r
for (int c = 0; c < m; c ++) { // 枚举当前列号c
now ^= 1;
memset(f[now], 0, sizeof(f[now]));
for (int k = 0; k < (1<<m); k ++) { // k表示上一个状态
/**
情况1:当前位置不放置木板,这种情况下要求 上一个状态的首个不确定格子是放置了木板的,
即: k & (1 << (m-1)) != 0
*/
if (k & (1 << (m-1))) { // 说明上一个状态的最前面的格子已填充
int s = (k << 1) ^ (1 << m); // s表示当前状态
f[now][s] += f[now^1][k];
}
/**
情况2:当前位置放置一块竖着放的木板,这种情况下要求
上一个状态的首个不确定格子是没有放置模板的,
即: k & (1 << (m-1)) == 0
*/
if (r > 0 && (k & (1 << (m-1))) == 0) { // 说明上一个状态的最前面的格子(即当前状态的上面的那个格子)未填充
int s = (k << 1) ^ 1; // s表示当前状态
f[now][s] += f[now^1][k];
}
/**
情况3:当前位置放置一块横着放的木板,这种情况下要求
上一个状态的最后一个不确定格子是没有放置模板的,
并且要求上一个状态的最前面一个不确定格子是必须放置模板的(此时不放,没有别的时间放!),
即: k & 1 == 0
*/
if (c > 0 && (k & 1) == 0 // 说明上一个状态的最后面的格子(即当前状态的左边的那个格子)未填充
&& (k & (1 << (m-1))) ) { // 说明上一个状态的最前面的格子已填充
int s = (k << 1) ^ 3 ^ (1 << m); // s表示当前状态
f[now][s] += f[now^1][k];
}
}
}
}
printf("%lld\n", f[now][(1<<m)-1]);
}
return 0;
}POJ2411 Mondriaan's Dream 题解 轮廓线DP
原文:https://www.cnblogs.com/quanjun/p/11960653.html