设 是有序集,且
,表示有序集 S 的二叉搜索树利用二叉树的结点来存储有序集中的元素。它具有下述性质:存储于每个结点中的元素 x 大于其左子树中任一结点所存储的元素,小于其右子树中任一结点所存储的元素。二叉搜索树的叶节点是形如
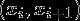 的开区间。在表示 S 的二叉搜索树中搜索一个元素 x ,返回的结果有两种情况:
的开区间。在表示 S 的二叉搜索树中搜索一个元素 x ,返回的结果有两种情况:
① 在二叉搜索树的内结点中找到 ,令其概率为
② 在二叉搜索树的叶节点中确定 ,令其概率为
。
表示 x 小于
的值的概率,
表示所有 x 大于
的值的概率,
表示 x 位于
和
值的概率。
显然,有 ,
,
,
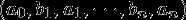 称为集合 S 的存取概率分布。
称为集合 S 的存取概率分布。
在表示 S 的二叉搜索树 T 中,设存储元素 的结点深度为
,叶节点
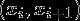 的结点深度为
的结点深度为 ,则
表示在二叉搜索树 T 中进行一次搜索所需的平均比较次数,p又称为二叉搜索树 T 的平均路长。在一般情况下,不同的二叉搜索树的平均路上是不相同的。
所以,最优二叉搜索树问题是对于有序集 S 及其存取概率分布 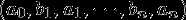 ,在所有表示有序集 S 的二叉搜索树中找出一颗具有最小平均路长的二叉搜索树。
,在所有表示有序集 S 的二叉搜索树中找出一颗具有最小平均路长的二叉搜索树。
二叉搜索树 T 的一棵含有结点 和叶节点
的子树可以看做是有序集
关于全集合
的一棵二叉搜索树,其存取概率为下面的条件概率
设 是有序集
关于存取概率
的一棵最优二叉搜索树,其平均路长为
。
的根结点存储元素
。其左右子树
和
的平均路长分别为
和
。由于
和
中结点深度是他们在
中的结点深度减1,所以得出
由于 是关于集合
的一棵二叉搜索树,故
。若
,则用
替换
可得到平均路长比
更小的二叉搜索树。这与
是最优二叉搜索树矛盾。故
是一棵最优二叉搜索树。同理,
也是一棵最优二叉搜索树。
因此最优二叉搜索树问题具有最优子结构性质。
#include <iostream> using namespace std; const int MaxVal=9999,n=5; double p[n+1] = {-1,0.15,0.1,0.05,0.1,0.2}; //搜索到内部节点的概率 double q[n+1] = {0.05,0.1,0.05,0.05,0.05,0.1}; //搜索到虚拟键的概率 int root[n+1][n+1]; //记录根节点 double w[n+2][n+2]; //子树概率总和 double e[n+2][n+2]; //子树期望代价 void optimalBST(int n) { int i,j,k,len; for (i=1;i<=n+1;++i) { w[i][i-1]=q[i-1]; e[i][i-1]=q[i-1]; } for(len=1;len<=n;++len) { for(i=1;i<=n-len+1;++i) { j=i+len-1; e[i][j]=MaxVal; w[i][j]=w[i][j-1]+p[j]+q[j]; for(k=i;k<=j;++k) { double temp=e[i][k-1]+e[k+1][j]+w[i][j]; if (temp<e[i][j]) { e[i][j]=temp; root[i][j]=k; } } } } } void printOptimalBST(int i,int j,int r) { int rootChild = root[i][j]; if (rootChild == root[1][n]) { printf("k%d 是根\n",rootChild); printOptimalBST(i,rootChild - 1,rootChild); printOptimalBST(rootChild + 1,j,rootChild); return; } if (j < i - 1) return; else if (j == i - 1) { if (j < r) printf("d%d 是 k%d 的左孩子\n",j,r); else printf("d%d 是 k%d 的右孩子\n",j,r); return; } else { if (rootChild < r) printf("k%d 是 k%d 的左孩子\n",rootChild,r); else printf("k%d 是 k%d 的左孩子\n",rootChild,r); } printOptimalBST(i,rootChild - 1,rootChild); printOptimalBST(rootChild + 1,j,rootChild); } int main() { optimalBST(n); cout << "最优二叉树结构:" << endl; printOptimalBST(1,n,-1); system("pause"); return 0; }
原文:https://www.cnblogs.com/VividBinGo/p/11960637.html