20182324 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结

教材学习内容总结

• 1、图 ( graph ) 由顶点 ( vertice ) 和边 ( edge ) 构成。一个图（Graph）是一个序偶<V, E>，记为G = <V, E>，其中：
  （ 1 ）V = { v1 , v2 , … , vn } 是有限非空集合，vi 称为结点，V 称为结点集。
  （ 2 ）E 是有限集合，称为边集。E 中的每个元素都是 V 中顶点偶对，称之为边。
  图中表示边的顶点对是无序的图是无向图 ( undirected graph )。图中的边是顶点的有序对的图称为有向图 ( directed graph，or digraph )

• 2、图的表示：图可以用文字符号表述，也可以用图形描述，有两种形式：
  （ 1 ）集合表示：对于一个图 G，如果将其记为 G = < V , E >，并写出 V 和 E 的集合表示，称为图的集合表示。
  （ 2 ）图形表示：用小圆圈表示 V 中的结点，用由 u 指向 v 的有向线段表示有向边 < u , v > ；无向线段表示无向边（ u , v ），称为图的图形表示。

• 3、如果图中的两个顶点之间有边连接，则称它们是邻接的 ( adjacent )。如果无向图中连接顶点的边数达到最大，则图为完全图 ( complete )。路径 ( path ) 是图中连接两个顶点的边的序列。如果无向图中任意两个顶点间都有路径，则无向图称为连通的 ( connected )。第一个顶点和最后一个顶点相同且边不重复的路径称为环 ( cycle )。有向图中的路径是连接图中两个顶点的有向边的序列。

• 4、顶点的度、出度、入度
  • 在无向图中：
    顶点 V 的度 = 与 V 相关联的边的数目
  • 在有向图中：
    顶点 V 的出度 = 以 V 为起点有向边数
    顶点 V 的入度 = 以 V 为终点有向边数
    顶点 V 的度 = V 的出度 + V 的入度
• 5、树就是图。有向树是一个有向图，其中指定一个元素为根，并具有下列特性：
  • 任何顶点到根都没有连接
  • 到达每个非根元素的连接都只有一个
  • 从根到每个顶点都有路径

• 6、图中的每条边上都有对应权值的图称为带权图 ( weighted graph )，有时也称为网络 ( network )

• 7、图的遍历一般有两种：类似于树的层序遍历的广度优先遍历 ( breadth-first traversal )，和类似于树的先序遍历的深度优先遍历 ( depth-first traversal )。图的深度优先遍历与广度优先遍历的主要差异在于用栈代替队列来管理遍历过程。
  
  

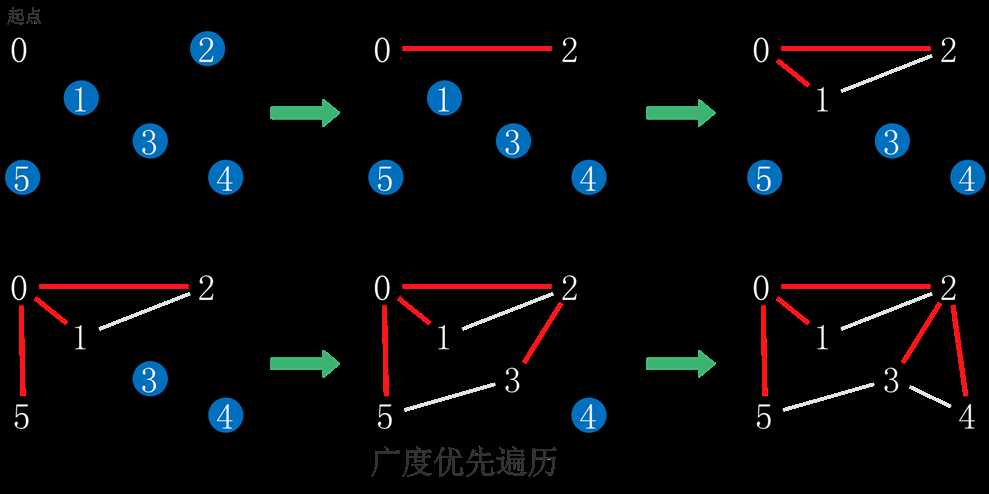
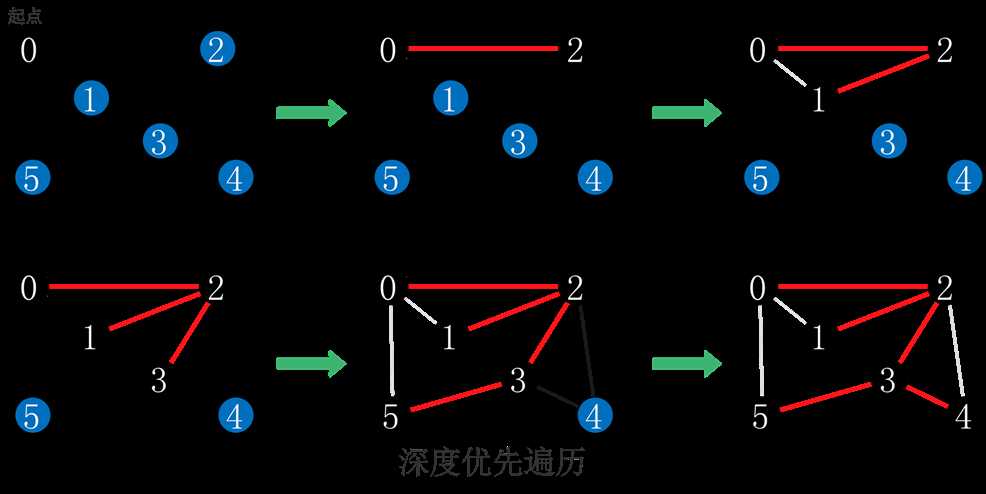
• 8、当且仅当从任意顶点开始的广度优先遍历中得到的顶点数等于图中所含的顶点数时，图是连通的。

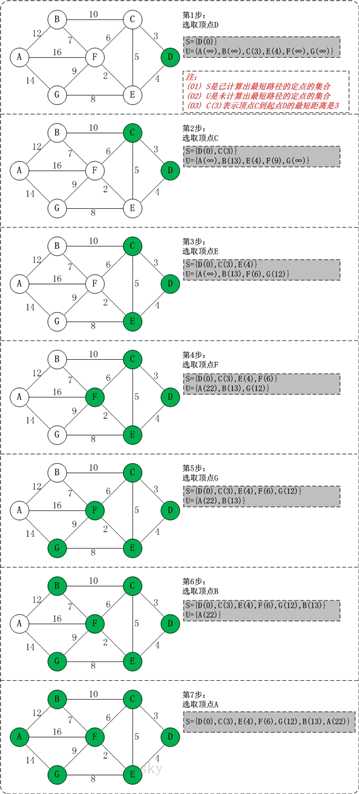
• 9、生成树 ( spanning tree ) 是包含图中所有顶点及图中部分（ 可能不是全部 ）边的一棵树。最小生成树 ( minimum spanning tree ) 是其所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树。

教材学习中的问题和解决过程

• 问题1：Dijkstra 算法讲解。
• 问题1解决方案：
  • 初始时，S只包含起点 s ；U 包含除 s 外的其他顶点，且 U 中顶点的距离为 “ 起点 s 到该顶点的距离 ” [ 例如，U中顶点v的距离为 ( s , v ) 的长度，然后 s 和 v 不相邻，则 v 的距离为 ∞ ]。
  • 从 U 中选出 “ 距离最短的顶点 k ” ，并将顶点 k 加入到 S 中 ；同时，从 U 中移除顶点 k 。
  • 更新 U 中各个顶点到起点 s 的距离。之所以更新 U 中顶点的距离，是由于上一步中确定了 k 是求出最短路径的顶点，从而可以利用 k 来更新其它顶点的距离；例如，( s , v ) 的距离可能大于 ( s , k ) + ( k , v ) 的距离。
  • 重复步骤 ( 2 ) 和 ( 3 ) ，直到遍历完所有顶点。
    
• 问题2：Floyd 算法讲解
• 问题2解决方案：
  • 从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
  • Floyd 算法过程矩阵的计算----十字交叉法
    方法：两条线，从左上角开始计算一直到右下角 如下所示
    给出矩阵，其中矩阵 A 是邻接矩阵，而矩阵 Path 记录 u , v 两点之间最短路径所必须经过的点
    
    计算方法如下：
    
    
    
    最后 A3 即为所求结果。

代码调试中的问题和解决过程

• 问题：怎么在 Android 中搭建数据库存储数据
• 问题解决方案：Android 提供了 SQLite 帮助我们管理数据库，它是一款轻型的数据库，主要用在嵌入式系统，它占用的资源非常低。SQLite 不依赖第三方软件，也不需要安装。数据库中的信息都包含在一个文件中，这个文件可以自由地复制到其它目录或其它机器上。我们可以使用 SQLiteOpenHelper 类来创建和更新数据库，使用 SQLiteDatabase 类实现对数据库中数据的添加、删除、查询和修改等功能。

代码托管

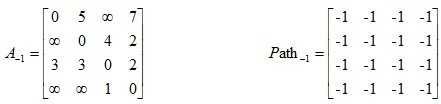
（statistics.sh脚本的运行结果截图）

上周考试错题总结

上周未进行考试，故无错题。

结对及互评

点评：

• 博客中值得学习的或问题：
  • 图文并茂，有参考资料
  • markdown 格式运用较为熟练
• 代码中值得学习的或问题：
  • 代码格式规范，合理使用空白，便于阅读
• 基于评分标准，我给本博客打分：14分。得分情况如下：
  • 1、正确使用Markdown语法（加1分）
  • 2、模板中的要素齐全（加1分）
  • 3、教材学习中的问题和解决过程（2分）
  • 4、代码调试中的问题和解决过程（1分）
  • 5、本周有效代码超过300分行的（加2分）
  • 6、其他加分：
    • 感想，体会不假大空的加1分
    • 进度条中记录学习时间与改进情况的加1分
    • 有动手写新代码的加1分
    • 代码Commit Message规范的加1分
    • 错题学习深入的加1分
    • 点评认真，能指出博客和代码中的问题的加1分
    • 结对学习情况真实可信的加1分
• 参考示例

点评过的同学博客和代码

• 本周结对学习情况

  • 20182329 2019-2020-1 《数据结构与面向对象程序设计》第 10 周学习总结

  • 结对学习内容
    • 学习图的有关知识，了解有向图和无向图的区别。
    • 学习带权图，学会计算带权图的算法，最佳的算法。
    • 学习图的遍历，如深度优先遍历和广度优先遍历。
    • 学习生成最小树的方法。
    • 学会生成图的邻接矩阵的方法，实现计算每个节点的出度入度方法。
    • 学会图的计算度的方法。

其他（感悟、思考等，可选）

随着学习的逐步深入，本学期的 Java 程序设计与数据结构课程也即将告一段落了，回顾过往，我们学习了 Java 的基本语法，学习了数据结构，也学习了 Android 程序的编写。一路上收获颇丰，希望在未来的学习道路上能够更加深入与熟练。

学习进度条

参考：软件工程软件的估计为什么这么难，软件工程 估计方法

• 计划学习时间:20小时

• 实际学习时间:30小时

• 改进情况：

(有空多看看现代软件工程 课件 软件工程师能力自我评价表)

参考资料

• 《Java程序设计与数据结构教程（第二版）》

• 《Java程序设计与数据结构教程（第二版）》学习指导

20182324 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结

原文：https://www.cnblogs.com/lolipop2019/p/11954484.html